[数据结构与算法]【LeetCode 二叉树专项】从前序与中序遍历序列构造二叉树（105）

文章目录

• • 1. 题目
  • • 1.1 示例
    • 1.2 说明
    • 1.3 限制
  • 2. 解法一（递归）
  • • 2.1 分析
    • 2.2 实现
    • 2.3 复杂度
  • 3. 解法二（迭代）

1. 题目

定一棵树的前序遍历 preorder 与中序遍历 inorder 。请构造二叉树并返回其根节点。

1.1 示例

• 示例 $1$ ：
  

• 输入： preorder = [3, 9, 20, 15, 7] ， inorder = [9, 3, 15, 20, 7]
• 输出： [3, 9, 20, null, null, 15, 7]

• 示例 $2$ ：

• 输入： preorder = [-1] ， inorder = [-1]
• 输出： [-1]

1.2 说明

• 来源： 力扣（LeetCode）
• 链接： https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

1.3 限制

• 1 <= preorder.length <= 3000 ；
• inorder.length == preorder.length ；
• -3000 <= preorder[i], inorder[i] <= 3000 ；
• preorder 和 inorder 均无重复元素；
• inorder 均出现在 preorder ；
• preorder 保证为二叉树的前序遍历序列；
• inorder 保证为二叉树的中序遍历序列。

2. 解法一（递归）

2.1 分析

实际上，本题和【LeetCode 二叉树专项】最大二叉树（654）十分类似，都是给定整数数组，要求构造二叉树，最简单的方式都是通过递归进行求解，并且在之前的那道题目中求解的核心方法签名为：

def _maximum_binary_tree(self, nums: List[int], start: int, stop: int) -> Optional[TreeNode]:

此处给定了两个序列，可仿照给出类似的求解方法签名为：

def _build_tree(self, preorder: List[int], inorder: List[int],
                pre_start: int, pre_stop, in_start: int, in_stop: int) -> Optional[TreeNode]:

其中 pre_start 和 pre_stop 以及in_start 和 in_stop 表示递归构建节点时所使用的 preorder 和 inorder 元素范围。

然而，本题和【LeetCode 二叉树专项】最大二叉树（654）不同之处在于，求解后者的过程中总是可以很直接地确定子节点（或子树）的 val 域及所需 nums 元素的范围，对于本题就没有那么直接了，例如：虽然根据前序遍历的规则可以很容易知道数组的第一个元素就是根节点的 val 取值，但是乍一看却无从得知后续哪一部分属于左子节点的 val 取值，哪一部分又属于右子节点的 val 取值。

对此，可以充分结合中序遍历的性质来间接确定，如下图所示：

• 首先，在通过 preorder 确定根节点的 val 域之后，可以找到其对应在 inorder 中的位置；
• 接着，根据中序遍历性质可知根节点左边的元素都是其左子树节点的 val 值，右边元素都是其右子树节点的 val 值。

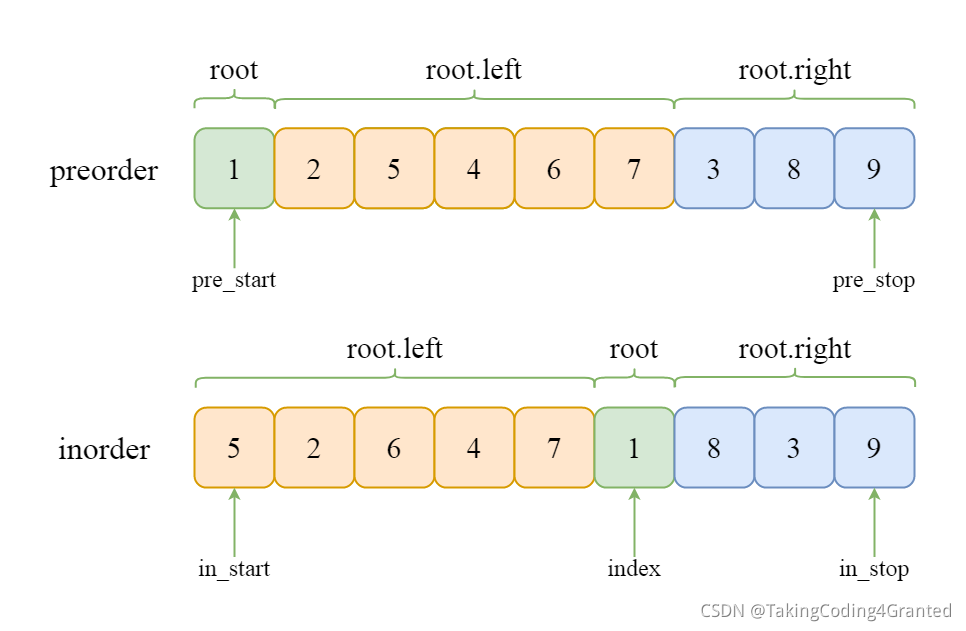
接着，在确定根节点的左子节点时，最重要是要确定 pre_start 和 pre_stop 以及in_start 和 in_stop 的最新一组值。结合上述分析，可得递归调用时确定 preorder 和 inorder 元素范围的索引如下图所示：

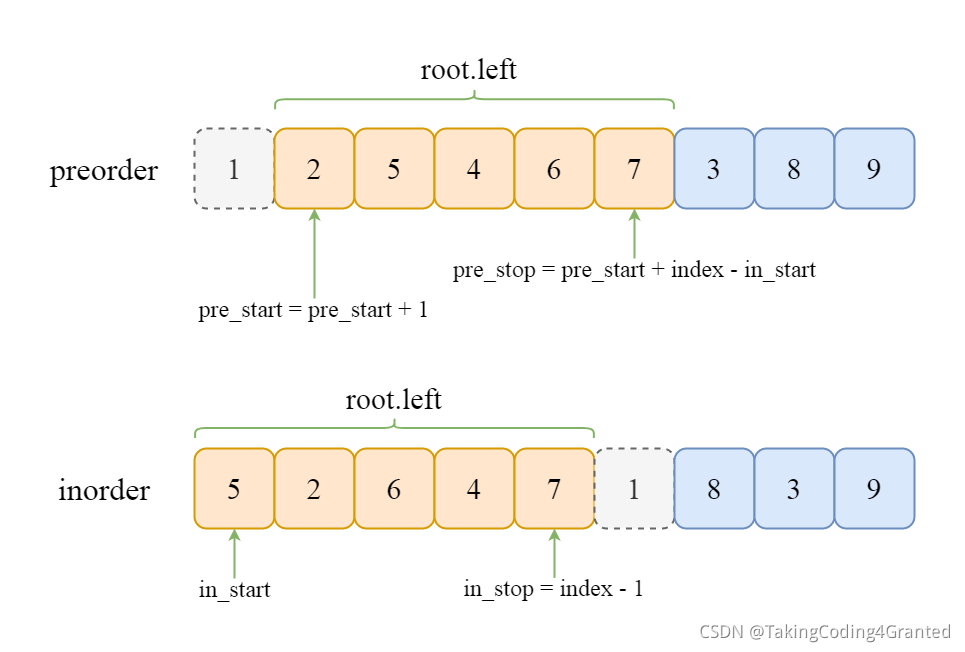
同理，在确定根节点的右子节点时，可得递归调用时确定 preorder 和 inorder 元素范围的索引如下图所示：

2.2 实现

from collections import deque
from typing import List, Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def _build_tree(self, preorder: List[int], inorder: List[int],
                    pre_start: int, pre_stop, in_start: int, in_stop: int) -> Optional[TreeNode]:
        if pre_start > pre_stop or in_start > in_stop:
            return
        index = inorder.index(preorder[pre_start], in_start, in_stop + 1)
        root = TreeNode(preorder[pre_start])
        root.left = self._build_tree(preorder, inorder,
                                     pre_start + 1, pre_start + index - in_start,
                                     in_start, index - 1)
        root.right = self._build_tree(preorder, inorder,
                                      pre_start + index - in_start + 1, pre_stop,
                                      index + 1, in_stop)
        return root

    def build_tree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        return self._build_tree(preorder, inorder, 0, len(preorder) - 1, 0, len(inorder) - 1)


def main():
    preorder = [3, 9, 20, 15, 7]
    inorder = [9, 3, 15, 20, 7]
    sln = Solution()
    root = sln.build_tree(preorder, inorder)

    tree = []
    visiting = deque([root])
    while visiting:
        node = visiting.popleft()
        if node:
            tree.append(node.val)
            visiting.append(node.left)
            visiting.append(node.right)
        else:
            tree.append(None)

    while True:
        if not tree[-1]:
            tree.pop()
        else:
            break

    print(tree)  # [3, 9, 20, None, None, 15, 7]


if __name__ == '__main__':
    main()

2.3 复杂度

• 时间复杂度： $O(n)$，其中 $n$ 是树中的节点个数。
• 空间复杂度： $O(n)$，除去返回的答案需要的 $O(n)$ 空间之外，我们还需要使用 $O(n)$ 的空间存储哈希映射，以及 $O(h)$（其中 $h$ 是树的高度）的空间表示递归时栈空间。这里 $h<n$，所以总空间复杂度为 $O(n)$ 。

3. 解法二（迭代）

• 作者： LeetCode-Solution