🐕 给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
输入：root = [2,1,3]
输出：true
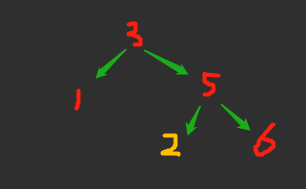
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
提示：
树中节点数目范围在[1, 104] 内
-2的31次方 <= Node.val <= 2的31次方 - 1
🐖 思路一：利用递归（中序遍历）加列表实现
以列表中第一个元素为基准，后面的数 如果比前面的数大，则return true ,每次更新pre的值
因为如果是搜索二叉树的话 中序遍历肯定是递增的…
上代码
public static boolean isValidBST(TreeNode root) {
// 列表存储 node结点 如果结点的val域是递增 则证明是搜索二叉树
List<TreeNode> list = new ArrayList<>();
process(root,list);
//以列表中第一个元素为基准，后面的数 如果比前面的数小，则return false ,否则每次更新num的值
int num = list.get(0).val;
for(int i = 1 ; i < list.size(); i++) {
if(list.get(i).val <= num) {
return false;
}else {
num = list.get(i).val;
}
}
return true;
}
public static void process(TreeNode node ,List<TreeNode> list) {
if(node == null) {
return;
}
// 下面 的递归(中序遍历)都是先左 再中 后右
process(node.left,list);
list.add(node);
process(node.right,list);
}
🐖 思路二：利用递归 加 范围判断
左子树的val 小于 root的val、右子树的val 大于 root的val、每次递归都要加上这个条件判断
为什么要加上范围判断呢，就是防止出现下面这种情况的发生，导致判断不准确
上代码
public static boolean isValidBST(TreeNode root) {
return process(root,Long.MIN_VALUE,Long.MAX_VALUE);
}
public static boolean process(TreeNode root,long min,long max) {
if(root == null) {
return true;
}
// 如果结点超过范围 return false
if(root.val <= min || root.val >= max) {
return false;
}
//左子树范围的最小值是min，最大值是当前节点的值，也就是root的值，因为左子树的值要比当前节点小
//右子数范围的最大值是max，最小值是当前节点的值，也就是root的值，因为右子树的值要比当前节点大
return process(root.left,min,root.val) && process(root.right,root.val,max);
}
🐖 思路三：中序遍历递归 + 判断值 是否递增（其实跟思路一是差不多的）
整一个 node 结点 代表 当前结点的前一个结点
上代码
public static TreeNode node;
public static boolean isValidBST(TreeNode root) {
if(root == null) {
return true;
}
//先判断左子树
if(!isValidBST(root.left)) {
return false;
}
// 如果 上一个结点的值 大于等于 当前结点的值 return false
if(node != null && node.val >= root.val) {
return false;
}
// 每次 node 要下移
node = root;
// 再判断右子树
if(!isValidBST(root.right)) {
return false;
}
return true;
}
但是这种方法过不了，我也是迷惑不解
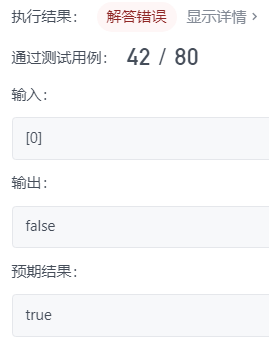如果有人会的话，还请不吝赐教~
🐖 思路四：中序遍历递归 + int值判断 是否递增（其实跟思路一和思路四是差不多的）
整一个Integer.MIN_VALUE 代表 结点的最小值 然后中序遍历 如果这个值不是递增的话 return false
上代码
public static int num = Integer.MIN_VALUE;
public static boolean isValidBST(TreeNode root) {
if(root == null) {
return true;
}
// 先判断 左树 是否 是完全二叉树
boolean isLeft = isValidBST(root.left);
if(!isLeft) {
return false;
}
// 判断结点值 是否递归排序
if(root.val <= num ) {
return false;
}else {
num = root.val;
}
// 再判断 右树 是否 是完全二叉树
return isValidBST(root.right);
}
但是这种方法 又 过不了，我又是迷惑不解
如果有人会的话，还请不吝赐教~