[数据结构与算法]Java实现TreeSet集合

Java实现TreeSet集合

Java中Set作为一个接口，有两种实现方式，一种是HashSet，另一种是TreeSet集合，此篇文章只讲解TreeSet的实现原理：
TreeSet是一种排序树，当我们随意插入数据后，TreeSet可以自动帮我们从小到大进行排序，事实上是调用了中序遍历二叉树的方法：

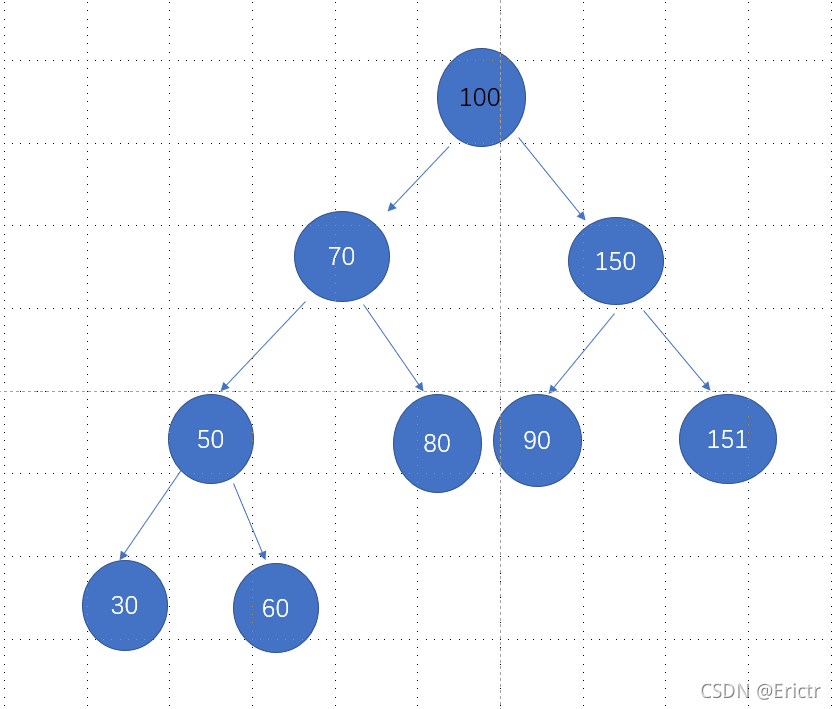
TreeSet的主要特点很明显，就是左子树上的数据一定全部都小于右子树上的数据，一般约定不存在重复数据，下面是具体的实现代码，一共大概300多行，不过其中有一部分是get和set方法，具体查看时，只需找到相应的功能部分即可，每一个功能模块我都给出来注释：

package collection.eric;
//import java.util.Scanner;
public class TreeSet {
	public static void main(String[] args) {
		BinaryTree binaryTree = new BinaryTree();
//		Scanner scan = new Scanner(System.in);
		//当输入"#"时，终止输入
//		while(true) {
//			String number = scan.next();
//			if(number == "#") {
//				break;
//			}
//			binaryTree.add(new TreeNode(Integer.parseInt(number)));
//		}
		binaryTree.add(new TreeNode(8));
		binaryTree.add(new TreeNode(4));		
		binaryTree.add(new TreeNode(10));
		binaryTree.add(new TreeNode(7));
		binaryTree.add(new TreeNode(11));
		binaryTree.add(new TreeNode(1));
		binaryTree.midOrder();
		boolean result = binaryTree.deleTreeNode(10);
		System.out.println(result);
		binaryTree.midOrder();
		
	}
}
//二叉树
class BinaryTree{
	private TreeNode root;
	
	public BinaryTree() {
		
	}
	public void setRoot(TreeNode root) {
		this.root = root;
	}
	//增加节点
	public void add(TreeNode node) {
		if(root == null) {
			root = node;
		}else {
			root.add(node);
		}
	}
	//前序遍历
	public void preOrder() {
		if(this.root != null) {
			this.root.preOrder();
		}else {
			System.out.println("当前二叉树为空，请先创建二叉树！！");
		}
	}
	//中序遍历
	public void midOrder() {
		if(this.root != null) {
			this.root.midOrder();
		}else {
			System.out.println("当前二叉树为空，请先创建二叉树");
		}
	}
	//后序遍历
	public void postOrder() {
		if(this.root != null) {
			this.root.postOrder();
		}else {
			System.out.println("当前二叉树为空，请先创建二叉树");
		}
	}
	//前序查找
	public boolean preSearch(int data) {
		boolean result = false;
		if(this.root != null) {
			result = this.root.preSearch(data);
		}
		return result;
	}
	//中序查找
	public boolean midSearch(int data) {
		boolean result = false;
		if(this.root != null) {
			result = this.root.midSearch(data);
		}
		return result;
	}
	//后序查找
	public boolean postSearch(int data) {
		boolean result = false;
		if(this.root != null) {
			result = this.root.postSearch(data);
		}
		return result;
	}
	//查找要删除的节点
	private TreeNode nodeSearch(int data) {
		if(this.root == null) {
			return null;
		}else {
			return this.root.nodeSearch(data);
		}
	}
	//查找要删除节点的父节点
	private TreeNode parentSearch(int data) {
		if(this.root == null) {
			return null;
		}else {
			return this.root.parentSearch(data);
		}
	}
	//删除并返回以treeNode为根节点的最小值
	private int deleTreeMin(TreeNode treeNode) {
		TreeNode target = treeNode;
		while(target.getLeft() != null) {
			target = target.getLeft();
		}
		int data = target.getData();
		deleTreeNode(target.getData()); 
		return data;
	}
	//删除节点
	public boolean deleTreeNode(int data) {
		if(this.root == null) {
			return true;
		}else {
			TreeNode targetNode = nodeSearch(data);
			if(targetNode == null) {
				return false;
			}
			if(this.root.getData() == data && this.root.getLeft() == null && this.root.getRight() == null) {
				this.root = null;
				return true;
			}
			TreeNode parentNode = parentSearch(data);
			//删除叶子节点
			if(targetNode.getLeft() == null && targetNode.getRight() == null) {
				if(parentNode.getLeft() != null && targetNode.getData() == parentNode.getLeft().getData()) {
					parentNode.setLeft(null);
					return true;
				}else if(parentNode.getRight() != null && targetNode.getData() == data) {
					parentNode.setRight(null);
					return true;
				}
			}else if(targetNode.getRight() != null && targetNode.getLeft() != null){//删除有两个子树的节点
				int minNumber = deleTreeMin(targetNode.getRight());
				targetNode.setData(minNumber);
			}else {
				if(targetNode.getLeft() != null) {
					if(parentNode.getLeft().getData() == data) {
						parentNode.setLeft(targetNode.getLeft());
						return true;
					}else if(parentNode.getRight().getData() == data) {
						parentNode.setRight(targetNode.getLeft());
						return true;
					}
				}else if(targetNode.getRight() != null) {
					if(parentNode.getLeft().getData() == data) {
						parentNode.setLeft(targetNode.getRight());
						return true;
					}else if(parentNode.getRight().getData() == data) {
						parentNode.setRight(targetNode.getRight());
						return true;
					}
				}
			}
		}
		return false;
	}
}
//树节点
class TreeNode{
	private int data;
	private TreeNode left;
	private TreeNode right;
	public TreeNode(){
		this.left = null;
		this.right = null;
	}
	public TreeNode(int data) {
		this.data = data;
	}
	public void setData(int data) {
		this.data = data;
	}
	public int getData() {
		return this.data;
	}
	public void setLeft(TreeNode left) {
		this.left = left;
	}
	public TreeNode getLeft() {
		return this.left;
	}
	public void setRight(TreeNode right) {
		this.right = right;
	}
	public TreeNode getRight() {
		return this.right;
	}
	//递归添加节点
	public void add(TreeNode node) {
		if(node==null){
			return;
		}
		if(node.data == this.data) {
			return;
		}
		if(node.data < this.data) {
			if(this.left == null) {
				this.left = node;
			}else {
				this.left.add(node);
			}
		}else {
			if(this.right == null) {
				this.right = node;
			}else {
				this.right.add(node);
			}
		}
	}
	//前序遍历二叉树
	public void preOrder() {
		System.out.print(this.data+" ");
		if(this.left != null) {
			this.left.preOrder();
		}
		if(this.right != null) {
			this.right.preOrder();
		}
	}
	//中序遍历
	public void midOrder(){
		if(this.left != null) {
			this.left.midOrder();
		}
		System.out.print(this.data+" ");
		if(this.right != null) {
			this.right.midOrder();
		}
	}
	//后序遍历
	public void postOrder() {
		if(this.left != null) {
			this.left.postOrder();
		}
		if(this.right != null) {
			this.right.postOrder();
		}
		System.out.print(this.data+" ");
	}
	//前序查找
	public boolean preSearch(int data) {
		
		if(this.data == data) {
			return true;
		}
		boolean result = false;
		if(this.left != null) {
			result = this.left.preSearch(data);
		}
		if(result == true) {
			return true;
		}
		if(this.right != null) {
			result = this.right.preSearch(data);
		}
		return result;
	}
	//中序查找
	public boolean midSearch(int data) {
		boolean result = false;	
		if(this.left != null) {
			result = this.left.midSearch(data);
		}
		if(result == true) {
			return true;
		}
		if(this.data == data) {
			return true;
		}
		if(this.right != null) {
			result = this.right.midSearch(data);
		}
		return result;
	}
	//后序查找
	public boolean postSearch(int data) {
		boolean result = false;
		if(this.left != null) {
			result =  this.left.postSearch(data);
		}
		if(result == true) {
			return true;
		}
		if(this.right != null) {
			result = this.right.postSearch(data);
		}
		if(result == true) {
			return true;
		}
		if(this.data == data) {
			return true;
		}
		return result;
	}
	//查找要删除的节点
	public TreeNode nodeSearch(int data) {
		if(this.data == data) {
			return this;
		}else if(this.data > data) {
			if(this.left != null) {
				return this.left.nodeSearch(data);
			}
			return null;
		}else {
			if(this.right != null) {
				return this.right.nodeSearch(data);
			}
			return null;
		}
	}
	//查找要删除节点的父节点
	public TreeNode parentSearch(int data) {
		if((this.left != null && this.left.data == data)||(this.right != null && this.right.data == data)) {
			return this;
		}else {
			if(this.data > data && this.left != null) {
				return this.left.parentSearch(data);
			}else if(this.data <data && this.right != null) {
				return this.right.parentSearch(data);
			}else {
				return null;
			}
		}
	}

	
}

此代码中较难部分的逻辑是删除节点的逻辑，删除节点时应该先找到要删除节点的父节点，然后在进行删除相应节点，一共需要考虑到三种情况：
1、删除叶子结点
算法：判断该节点是父节点的左子节点还是右子节点
若是左子节点，则parentNode.setLeft(null);
若是右子节点，则parentNode. setRight(null);
假设我们要删除60

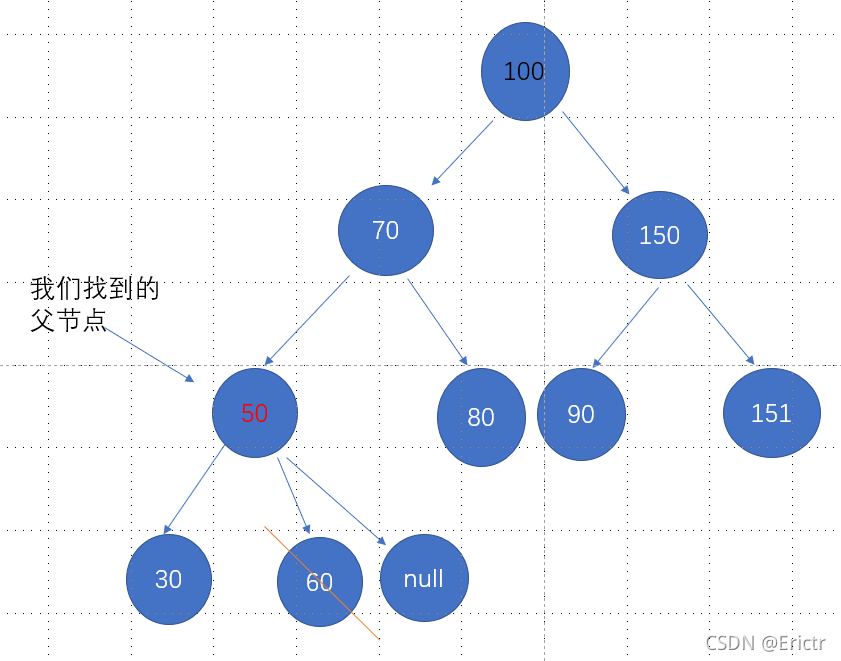
2、删除只有一个子节点的结点
算法：a.若要删除的节点为父节点的左子节点
1）该节点具有一个左子节点
parentNode.setLeft(targetNode.getLeft());
假设我们要删除50

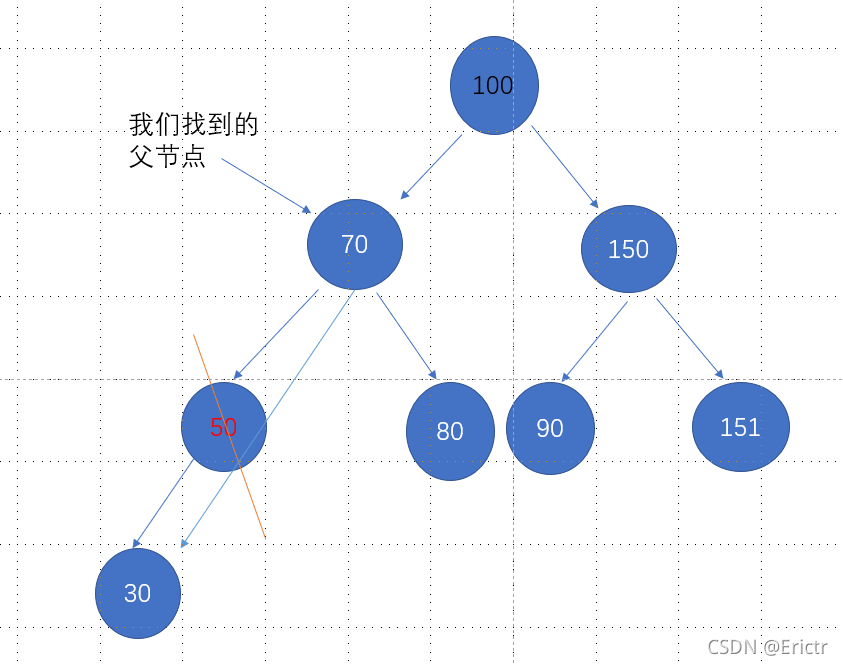
2. 该节点具有一个右子节点
   parentNode.setLeft(targetNode.getRight());
   
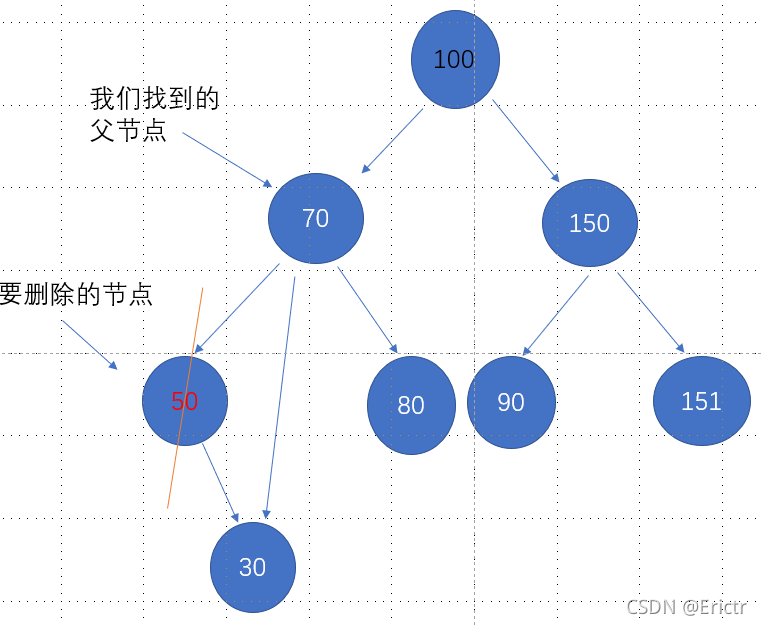
   b.要删除的节点是父节点的右子节点
   1）该节点有一个左子节点
   parentNode.setRight(targetNode.getLeft());
   targetNode
   这个和上面两个类似，画图太累就不画了，理解就Ok
   2）该节点有一个右子节点
   parentNode.setRight(targetNode.getRight());
   3、删除有两个子节点的节点
   算法：这个逻辑相对来说较简单，就是找到该节点的左子树中的最大值或者右子树中的最小值，然后替换该节点的data，然后利用我们写的函数删除这个最大值或者最小值所对应的节点。
   这里我们假设要删除70
   
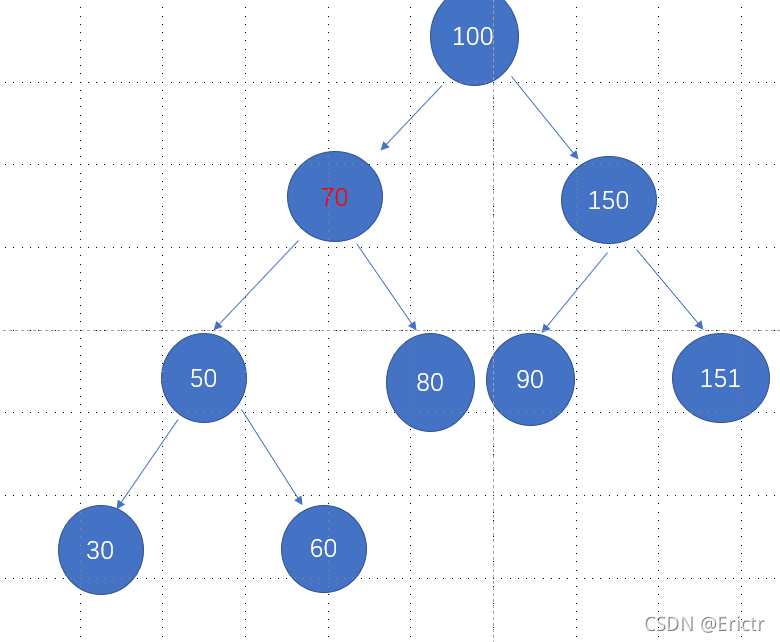
   我们直接找到左子树的最大值60或者右子树的最大值80，对目标节点进行替换，然后删除该节点即可。

二叉树的内容比较多，大家一起学习，Fighting！！！