线性查找
基本思想:按照顺序,进行挨个比对,找到要查找的值,则将其下标或者他的值返回
代码实现:
public static int seqSearch(int[] arr ,int value) {
//arr为目标数组,value为目标查找数据
for(int i = 0;i < arr.length;i++) {
if(arr[i] == value) {
return i;
}
}
return -1;
}
二分查找
使用二分查找的一个前提就是,所给的数据序列必须是有序的
二分查找思路分析:
1,首先确定还数据序列中间的下标【int mid = (left + right)/2】
2,然后让目标值(value)和这个中间值进行比较
3,如果目标值(value)大于中间值(mid),那么就在中间值的右边进行递归查找,
4,如果目标值(value)小于中间值(mid),那么就在中间值的左边进行递归查找
5,如果目标值(value)等于中间值(mid),那么就说明目标值已经找到,按照要求返回下标
代码实现:
public static int binarySearch(int[] arr,int left,int right,int value) {
//确定此次查找时的中间值是多少
int mid = (left + right) /2;
//如果左指针大于右指针那么就说明没有找到
if(left > right) {
return -1;
}
//如果要找的值比中间值小,那么就在左半边继续找
if(value < arr[mid]) {
return binarySearch(arr,left,mid-1,value);
}
//如果要找的值比中间值大,那么就在右半边继续找
else if(value > arr[mid]) {
return binarySearch(arr,mid+1,right,value);
}
//如果中间值就等于要找得值,那么就把目标值所在得下标返回
else if(value == arr[mid]){
return mid;
}
//如果走到了这一步那么就说明没有找到目标值
return -1;
}
变式,如果带查找的数列中存在多个需要查找的值,该如何实现
1,在找到目标值之后,向保目标值的左边和右边分别进行扫描,直到找到其值不等于目标值就结束扫描,将扫描的值等于目标值得下标存进集合里面,最后返回集合。
代码实现:
public static ArrayList<Integer> binarySearch(int[] arr, int left, int right, int value) {
//确定此次查找时的中间值是多少
int mid = (left + right) /2;
//如果左指针大于右指针那么就说明没有找到,则返回一个空集合
if(left > right) {
return new ArrayList<>();
}
//如果要找的值比中间值小,那么就在左半边继续找
if(value < arr[mid]) {
return binarySearch(arr,left,mid-1,value);
}
//如果要找的值比中间值大,那么就在右半边继续找
else if(value > arr[mid]) {
return binarySearch(arr,mid+1,right,value);
}
//如果中间值就等于要找得值,那么就把目标值所在得下标返回
else if(value == arr[mid]){
int flag = mid;
//创建一个集合
ArrayList<Integer> arr1 = new ArrayList<Integer>();
//往mid的左边进行扫描
while(true) {
if(flag < 0 || arr[flag] != value) {
break;
}
arr1.add(flag);
flag--;
}
//因为上面已经扫描过mid所以现在mid不能再被扫描,否则会重复
flag = mid+1;
//往mid的右边进行扫描
while(true) {
if(flag > arr.length-1 || arr[flag] != value) {
break;
}
arr1.add(flag);
flag++;
}
return arr1;
}
//如果走到了这一步那么就说明没有找到目标值,返回一个空集合
return new ArrayList<>();
}
插值查找
插值查找注意事项:
(1)对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找,速度较快
(2)关键字分布不均匀的情况下,该方法不一定比折半查找要好。
插值查找基本思想:插值查找算法类似于二分查找,不同的是插值查找每次从自适应mid出开始查找,将折半查找中的求mid索引公式,low表示左边索引left,hight表示右边索引right,key就是前面我们讲的目标值(value)
公式:int mid = low +(hight - low)*(key - arr[low])/(arr[hight] - arr[low])

算法实现:
public static int insertValueSort(int[] arr,int left,int right,int value) {
if(left > right || value > arr[right] || value < arr[left]) {
return -1;
}
int mid = left + (right - left)*(value-arr[left])/(arr[right] - arr[left]);
if(value < mid) {
return insertValueSort(arr,left,mid-1,value);
}
else if(value > mid) {
return insertValueSort(arr,mid + 1,right,value);
}
else {
return mid;
}
}
费波那契查找(黄金分割法)
斐波那契(黄金分割法)原理:
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,
即mid = low + F[k - 1] - 1(F代表斐波那契数列)
对F(k - 1) - 1的理解:
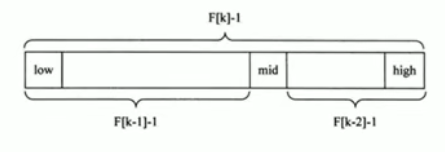
(1):由斐波那契数列F[k] = F[k-1] + F[k-2]的性质,可以得到(F[k] - 1)= (F[k-1] - 1) + (F[k-2] - 1) + 1。该式说明,只要顺序表的长度为F[k] - 1,则可以将该表分成长度为F[k-1] - 1和F[k-2] - 1的两段。即如上图所示,从而中间位置为mid = low + F[k-1] - 1
(2):类似的,每一子段可以用相同的方式分割
(3):但顺序表长度n不一定刚好等于F[k] - 1,所以需要将原来的顺序表长度增加至F[k] - 1.这里的k值只要能使得F[k] - 1恰好大于或等于n即可,由以下代码得到,顺序表长度增加后,新增的位置(从n+1到F[k] - 1位置),都赋为n位置的值即可
while(n > fib(k) - 1) {
k++;
}
代码实现:
//用非递归的方式得到斐波那契数列
public static int[] fi(int MaxSize) {
int[] f = new int[MaxSize];
f[0] = 1;
f[1] = 1;
for(int i = 2;i < MaxSize;i++) {
f[i] = f[i-1] + f[i-2];
}
return f;
}
public static int fiSearch(int[] a,int key) {
int low = 0;
int high = a.length-1;
int k = 0;//表示斐波那契分割数值的下标
int mid = 0;//存放mid
int[] f = fi(20);//表示斐波那契数列
//获取到斐波那契分割数值的下标
while(high > f[k]-1) {
k++;
}
//因为f[k]值可能大于a的长度,因此我们需要使用Arrays类,一个新的数组,并指向a[]
int[] temp = Arrays.copyOf(a,f[k]);
for(int i = high+1;i < temp.length;i++) {
temp[i] = a[high];
}
//使用while来循环处理,找到key
while(low <= high) {
mid = low + f[k - 1] - 1;
if(key < temp[mid]) {//我们应该继续向数组的前面查找
high = mid - 1;
k--;
}else if(key > temp[mid]) {//我们应该继续向数组的后面查找(右边)
low = mid + 1;
k -= 2;
}else {//需要确定返回的是哪个下标
if(mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}