此篇文章中的二叉搜索树基本操作包括了建树、插入节点、删除节点以及这些操作引申出来的题。
再回头看之前的二叉搜索树笔记,其实考点就蕴含着这些基础中啊。
文章目录
一、BST插入
基础复习
Bintree insert(Bintree BST,int x)
{
if(!BST)
{
BST=(Bintree)malloc(sizeof(struct node));
BST->data=x;
BST->left=BST->right=NULL;
}
else
{
if(BST->data>x)
{
insert(BST->left,x);
}
else if (BST->data<x)
{
insert(BST->right,x);
}
}
return BST;
}
在BST中插入值是不需要改变树的结构的。
如果遇到一个空结点就直接插入即可,非空结点则根据性质向左或者向右继续查找空位。
701. 二叉搜索树中的插入操作
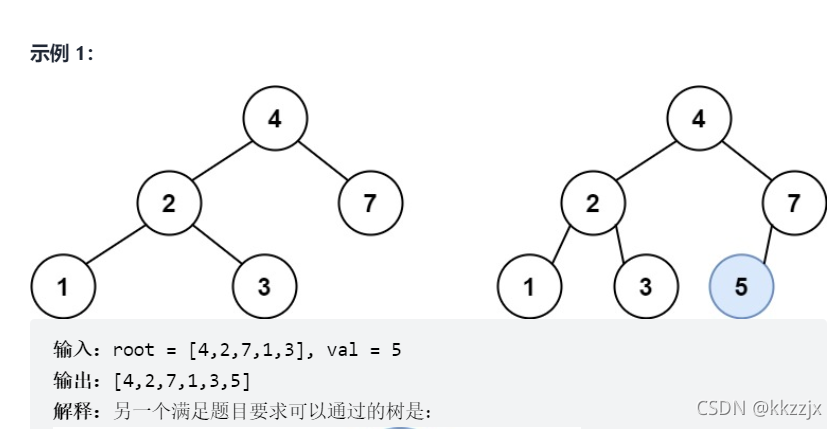
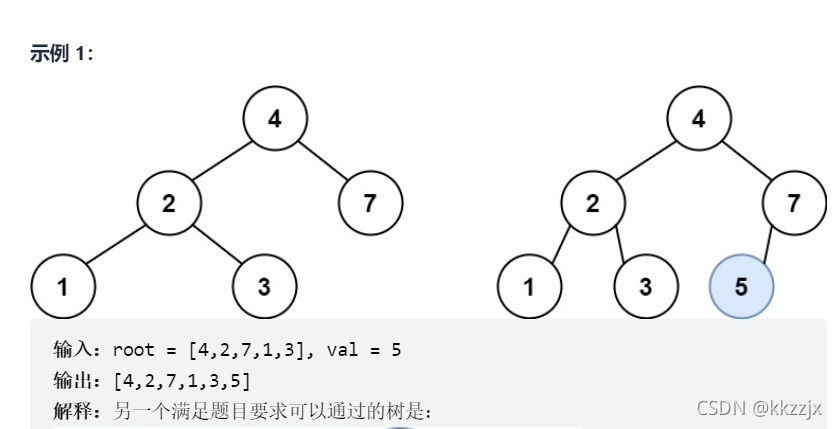
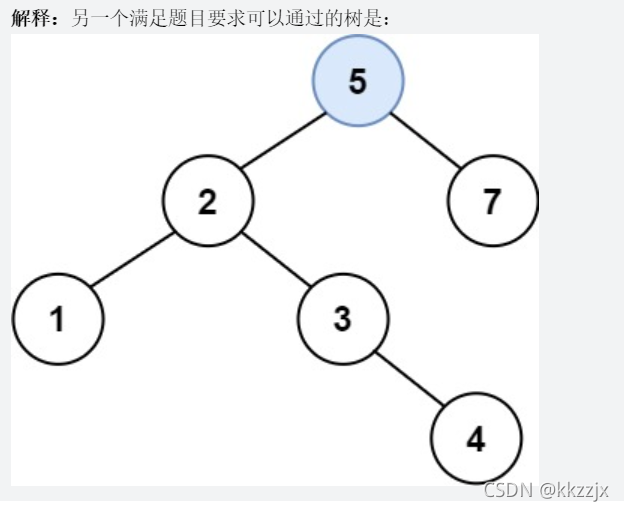
题目示例中的另一种解法改变了树的结构,其实不必被此干扰…
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root==nullptr)
{
root=new TreeNode(val);
}
if(val<root->val)
{
root->left=insertIntoBST(root->left,val);
}
else if(val>root->val)
{
root->right=insertIntoBST(root->right,val);
}
return root;
}
二、BST中寻找最大最小结点
这是做结点删除的前置内容~
一直向左搜索可以获得最小结点;一直向右搜索可以获得最大结点。
Bintree FindMax(Bintree BST)
{
if(!BST) return NULL;
else if(BST->right==NULL) return BST;
else return FindMax(BST->right);
}
Bintree findmin(Bintree BST)
{
if(BST)
{
while(BST->left)
{
BST=BST->left;
}
return BST;
}
}
三、BST结点删除
三种情况
1.删除的是叶结点
2.删除的结点只有一个孩子结点
3.删除的结点有左右两颗子树,那么要转换为第二种情况:选取左子树中的最大元素或者右子树的最小元素(利用上面讲的findmax和findmin函数)
450. 删除二叉搜索树中的节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root==nullptr) return nullptr;
if(root->val==key){
if(root->left==nullptr) return root->right;
else if(root->right==nullptr) return root->left;
else{
//右子树中找最小
TreeNode* cur=root->right;
//一直向左寻找...
while(cur->left!=nullptr)
{
cur=cur->left;
}
if(cur!=nullptr) root->val=cur->val;
root->right=deleteNode(root->right,root->val);
return root;
}
}
if(key<root->val)
{
root->left=deleteNode(root->left,key);
}
if(key>root->val)
{
root->right=deleteNode(root->right,key);
}
return root;
}
};
四、通过序列建树
模版题~ 根据树的后序(前序)、中序序列建树
106.从中序与后序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(inorder.size()==0||postorder.size()==0) return nullptr;
else
{
return create(0,inorder.size()-1,0,postorder.size()-1,inorder,postorder);
}
}
TreeNode* create(int inL,int inR,int postL,int postR,vector<int>& inorder,vector<int>& postorder)
{
if(inL>inR||postL>postR) return nullptr;
TreeNode* root=new TreeNode(postorder[postR]);
int mid;
for(int i=inL;i<=inR;i++)
{
if(inorder[i]==postorder[postR])
{
mid=i;//1
break;
}
}
int rightLength=inR-mid;//3
root->right=create(mid+1,inR,postR-rightLength,postR-1,inorder,postorder);
root->left=create(inL,mid-1,postL,postR-rightLength-1,inorder,postorder);
return root;
}
};
找出分割结点,然后递归左区间和右区间进行建树
相同思路题:
108.将有序数组转换为二叉搜索树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
int n=nums.size();
if(n==0) return nullptr;
return createBST(0,n-1,nums);
}
TreeNode* createBST(int L,int R,vector<int>& nums)
{
if(L>R) return nullptr;
int mid=(L+R)/2;
TreeNode* root=new TreeNode(nums[mid]);
root->left=createBST(L,mid-1,nums);
root->right=createBST(mid+1,R,nums);
return root;
}
};