- 善用算法是培养程序设计逻辑很重要的步骤,许多实际的问题都可用多个可行的算法来解决,本章重点向大家介绍了分治法在解决问题上的重大作用。
🎆分治法
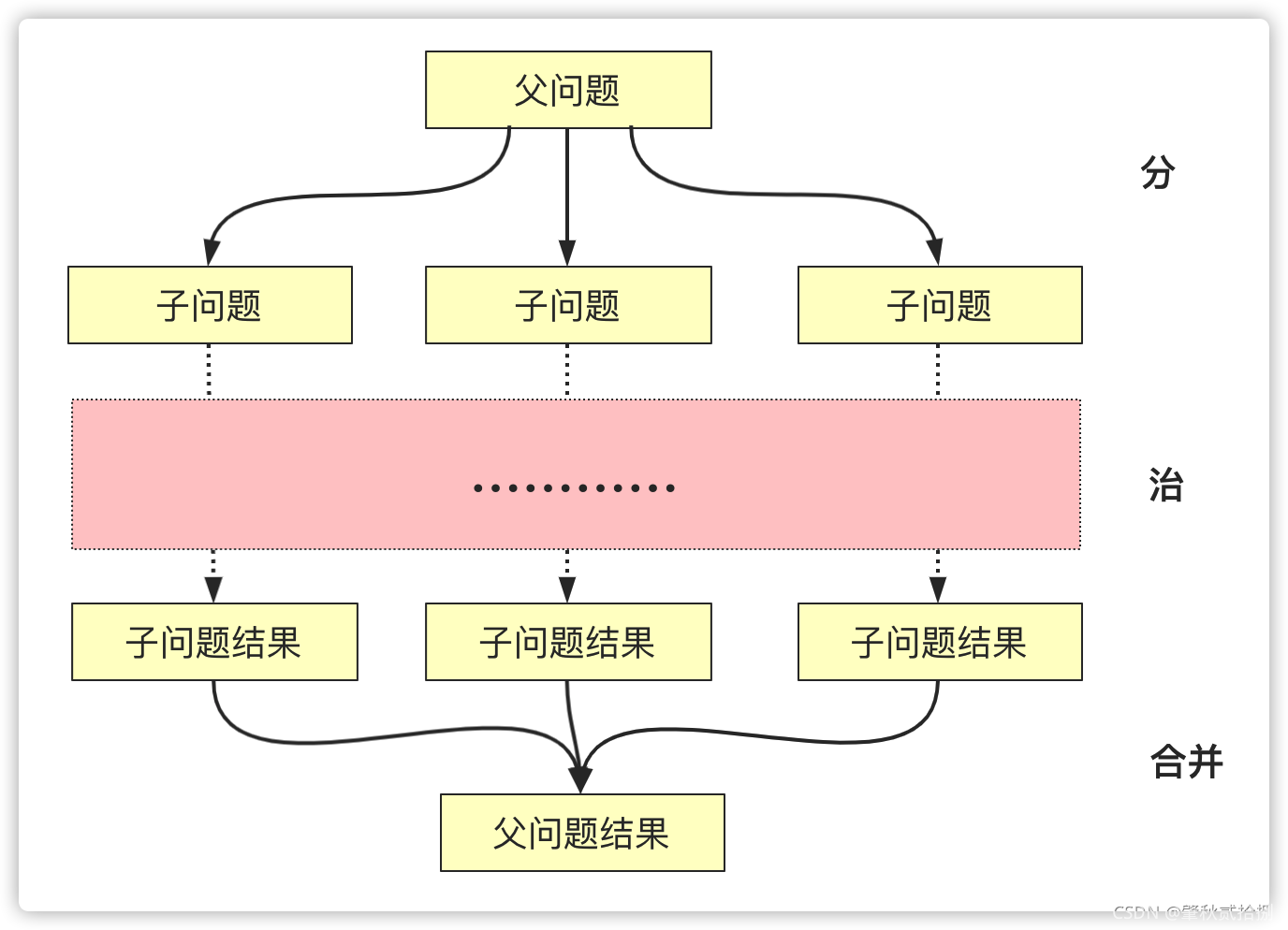
- 定义:分治法也被称为分而治之法,是一种很重要的算法,我们可以利用分治法来逐一拆解复杂的问题,核心思想是将一个难以解决的大问题依照相同的概念分割成两个或更多的子问题,以便各个击破。
- 应用:分治法的应用范围相当广泛,如快速排序法,递归算法,大整数乘法,二分查找,归并排序等等,这些耳熟能详的问题当中它都扮演这极为重要的地位。
- 过程:1.分解(将问题分成若干个互相独立的与原问题相同的子问题)2.解决(将子问题分解到容易解决)3.合并(将已求解的各个子问题的解逐步合并为原问题的解)
🎇 了解时间复杂度
-
那么说到算法,所有学习算法的人都应该适当了解时间复杂度O(f(n))的概念,因为时间复杂度是用来评估一个算法好坏的标准之一,下面让我们简单了解下时间复杂度
-
定义:在一个完全理想状态下的计算机中,我们定义T(n)来表示程序执行所需要花费的时间,其中n代表数据输入量。f(n)表示执行与算法优劣和问题规模有关的执行数,O的作用则是去除其他项,包括与最高项相乘的常数,只保留最高项。
-
f(n)=2n2+1 - - > O(f(n))=O(n2)
-
f(n)=n2/10+2n - - > O(f(n))=O(2n)
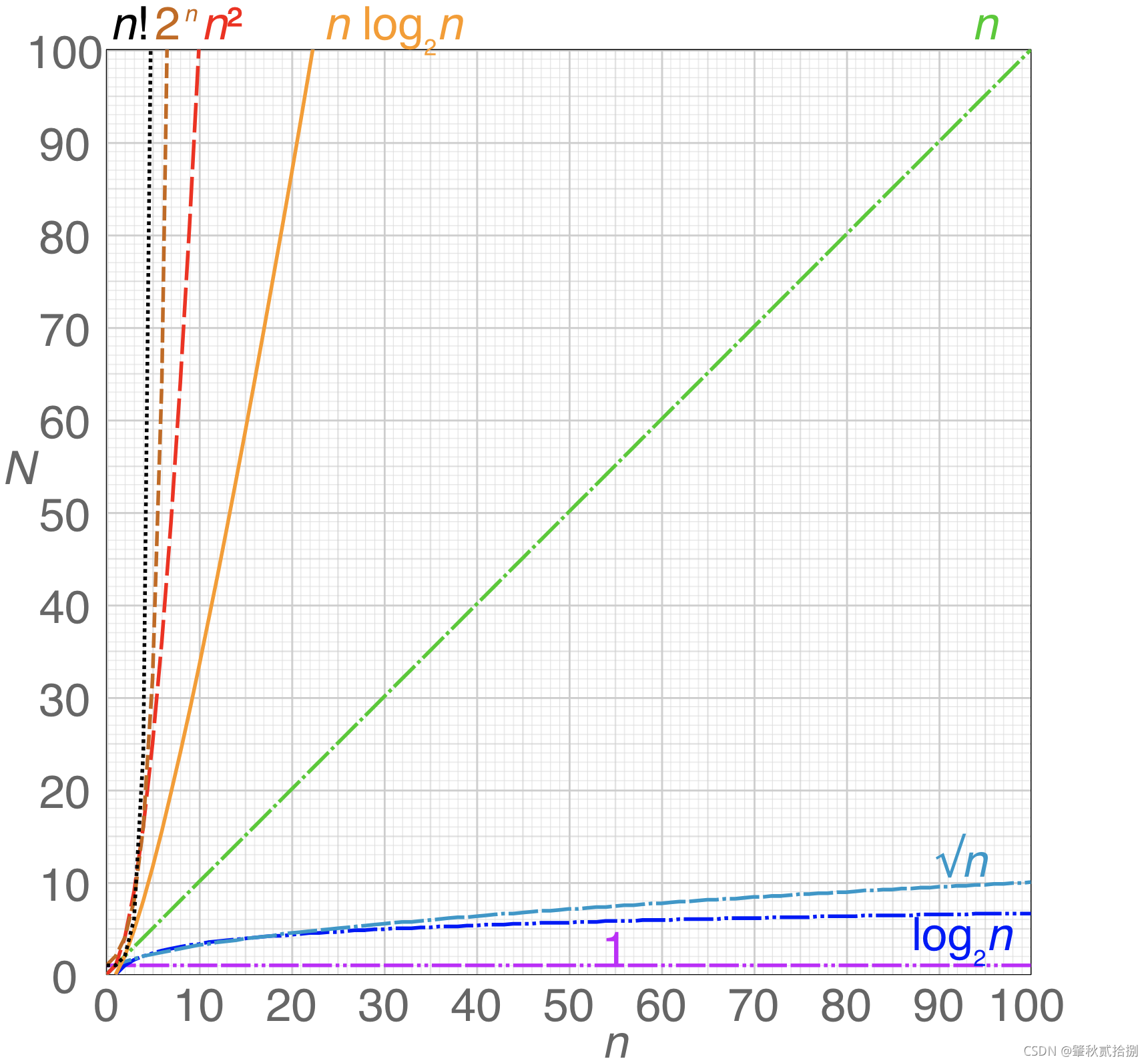
- 下面是关于时间复杂度优劣的排序

? 分治法正在磨刀——二分查找
- 二分查找又叫做折半查找,不断将问题缩小为之前的一半,通过中间的元素和要查找的元素进行对比,然后对问题继续分解和治理的这么一个过程,直到找到数或退出循环为止。
步骤:
1.先确定一个合适的数据结构(这里以数组来说明)。设置数组a[size]来存放size个已经排好序的元素。
2.同时定义两个变量left和right来表示该数组的下节和上界。并进行初始化left=0,right=size-1;
3.定义一个中间值middle=(left + right)/2;
4.判断条件为low小于等于right是否成立。
5.判断a[middle]和key是否相同,相同则算法结束,输出key。不相同则判断,如果a[middle] < key , 则low + 1 ; 否则 right - 1 , 继续判断 - 代码如下:
#include<stdio.h>
#define size 10
int main(void) {
int a[size] = {2,7,12,15,21,22,29,34,36,41};
int key, middle;
int left=0, right=size-1;
scanf("%d", &key);
while (left <= right) {
middle = (left + right) / 2;
if (a[middle] == key) {
printf("在数列第%d位中找到了%d", middle+1, key);
break;
}
else if (a[middle] < key)
left = middle + 1;
else
right = middle - 1;
}
if (left > right)
printf("在数列中没有找到当前数");
}
?分治法向你重拳出击——归并排序
- 归并排序在于把一个无序的数列进行拆分,拆分成很多个数列,并对这些数列进行排序,使之成为有序数列,然后合并两个有序数列,依次往上推。
- 那么如何合并两个有序数列? 只要比较两个数列的第一个数,谁小取谁,再把这个数从对应序列删去,直到其中一个数列为空为止。
#include<stdio.h>
int mergesort(int a[],int b[],int left,int right);//归并排序中分隔的函数
int merges(int a[],int t[],int left,int mid,int right);//归并排序中合并的函数
int main(void) {
int a[1000];//定义一个数列
int n;//人为要求数列的长度
int i;
scanf("%d", &n);
printf("放入需要排序的数列:");
for (i = 0;i < n;i++)
scanf("%d", &a[i]);
i = 0;
mergesort(a, a , i , n-1);//1.刚开始为一整个数列长度left,right为上下界 2.为什么传两个a数组进去?需要创建一个新数列来放排序后的数列
printf("排完后的数列为:");
for (i = 0;i < n;i++)
printf("%d ", a[i]);
}
int mergesort(int a[],int t[] ,int left,int right) {//利用分隔的思想,把当前数列不断分成两半
int mid;
int sor[1000];//新的数组用来放合并后的新数列
if (left == right) {//表示分到最后只剩下一个数,运用的是递归的思想
t[left] = a[right];//将a数组的所有值放入了sor中
}
else {
mid = (left + right) / 2;
mergesort(a,sor, left, mid);//对左边的继续分割
mergesort(a,sor, mid + 1, right);//对右边的继续分割
//函数做合并时,也是借助mergesort回去
merges(sor, t, left, mid, right);//对当前范围内的两个数列进行合并
}/*——————在倒数第二层做merges函数时,sor是最底层if语句满足时的t(a数组的赋值),t是再上一层传下来的sor,merges改变的是上一层的sor(这一层的t)的顺序*/
/*——————当你传到只剩两个的时候,做最后一遍merges,而这里的t是外面的a,所以改变外面a的值*/
return 0;
}
int merges(int a[], int t[], int left, int mid, int right) {//把两个数列第一项进行比较,最小的放到一个新数组,并在当前数列删去这个
//a为原数组,t为合并排序后的新数组
int i = left, j = mid + 1, k = left;//i表示第一个数列的上界,j表示第二个数列的上界,k表示合并数列的第一数
while (i <= mid && j <= right) {//判断两个数列都还有数
if (a[i] <= a[j]) {
t[k] = a[i];
i++;
k++;
}
else {
t[k] = a[j];
j++;
k++;
}
}//小的值放入
while (i <= mid)//两个while用来把剩下的数放入t新数组
t[k++] = a[i++];
while (j <= right)
t[k++] = a[j++];
return 0;
}
- 递归的思想在分治法中也是处处体现,要搞清楚分解问题和合并问题时需要的步骤。
- 代码块中/**/的内容是整个问题最主要的思想,分析了合并的步骤,以及每个参数在问题之中的作用。
?分治法对你进行了降维打击——汉诺塔问题
-
汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则:
(1)每次只能移动柱子最顶端的一个圆盘;
(2)每个柱子上,小圆盘永远要位于大圆盘之上 -
很显然在汉诺塔问题的解决中,思想也是运用了递归和分治法(递归和分治法就像一对孪生兄弟,思想都是将复杂问题简单化)。
-
在只有三根柱子的时候,步骤为把两个盘子由A移到B;把第三个盘子A移到C;把两个盘子从B移动到C
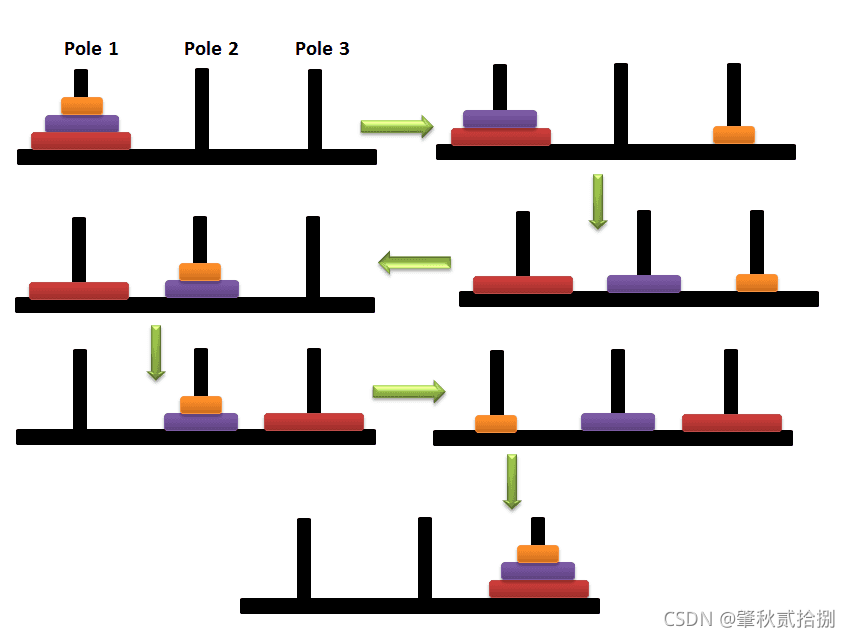
而当有n个盘子时,它的思想也是一样的,步骤为:
- 将A柱上的n-1个盘子借助C柱移向B柱
- 将A柱上仅剩的最后一个盘子移向C柱
- 将B柱上的n-1个盘子借助A柱移向C柱
- 根据前面的分析和图解,大家可以发现汉诺塔问题非常适合用递归和分治结合的方式来求解。因为汉诺塔问题满足了递归的两大特性。1.有反复执行的过程。2,有退出递归的出口。
- 再通过分而治之的想法,先相通只有几个盘子的情况,推出之间的关系式,推广到整体。
本章不重点展示汉诺塔的代码,想要了解可以关注后续博客。
🥇写在结尾
- 算法作为学习计算机科学程序设计领域的核心理论之一,它不仅存在于屏幕之后,在我们的生活中也是处处体现,本章借助分治法敲开算法的大门,让我们了解了妙趣横生的算法。但显然这只是算法领域的冰山一角,剩下的奇妙还等待着我们继续去探索。