[数据结构与算法] 回溯算法DFS应用

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 回溯算法DFS应用 -> 正文阅读

[数据结构与算法]回溯算法DFS应用

文章目录

一、算法思想

回溯算法实际上是将多叉树结构的问题，采用类似枚举的方式，把问题的所有可能性全部罗列出来。当在搜索的过程中发现不满足给定条件的选项，就将该分支去掉，这个操作通常被称为“剪枝”，再回退到上一步（回溯），尝试别的路径，直到最后找完所有路径。

二、应用分类

排列问题：N个数按照一定规则全排列，有几种排列方式；
组合问题：N个数里面按一定规则找出K个数的集合；
切割问题：一个字符串按一定规则有几种切割方式；
子集问题：一个N个数的集合里有多少符合条件的子集；
棋盘问题：N皇后，岛屿问题；

三、经典例题

1. 排列问题

给定N个数或者长度为N的字符串，输出所有排列方式。排列问题输出的每一种排列方式长度都与原长度相等。

伪代码

void DFS(){
    if(start == str.length-1){ //搜索到叶子节点
    	//去重判断
    	result.add(str);  //存放结果
        return;
    }
    for(i = start; i < str.length; i++){ //start下标用于缩小范围
    	swap(str,start,i); //处理节点
        DFS(start+1);  //下一层DFS
        swap(str,start,i);  //回溯
    }
}

1.1 字符串的全排列

leetcode：字符串的全排列

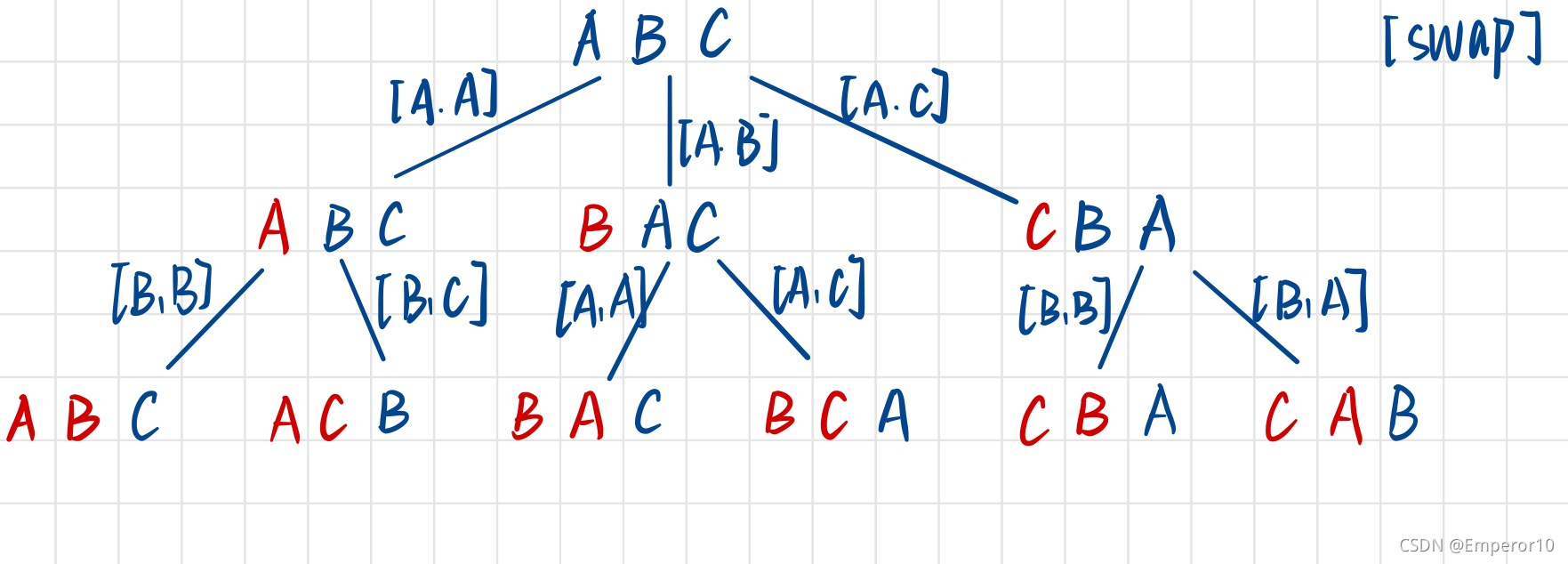
思路： 我们可以将字符串看成两部分，第一部分是以哪个字符开头，第二部分就是子问题。
定义一个start遍历字符串，使每个字符都做一遍开头，直到start 指向最后一个字符，说明已经当下已经排完，递归返回。
将start位置的字符分别和后面的所有字符进行交换（包括start位置）来实现不同的排列方式。

在这里插入图片描述

import java.util.ArrayList;
public class Solution {
    public void swap(char[] str,int x,int y){
        char temp = str[x];
        str[x] = str[y];
        str[y] = temp;
    }
    //当前这一步的处理逻辑
    public void DFS(char[] str,int start, ArrayList<String> result){
        //1. 退出条件
        if(start == str.length - 1){
        //valueOf(char[] data): 返回 char 数组参数的字符串表示形式
            String s = String.valueOf(str);
            //去重操作
            if(!result.contains(s)){
                //result.add(new String(str));
                result.add(s);
                return;
            }
        }
        //2. 尝试当下的每一种可能,剪枝
        for(int i = start; i < str.length; i++){
            swap(str,i,start);
            //3. 下一步DFS
            DFS(str,start+1,result);
            //4. 回溯
            swap(str,i,start);
        }
    }
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> result = new ArrayList<>(); //结果集
        if(str.length() == 0) return result;
        DFS(str.toCharArray(),0,result);
        return result;
    }
}

1.2 数组全排列

leetcode：数组全排列

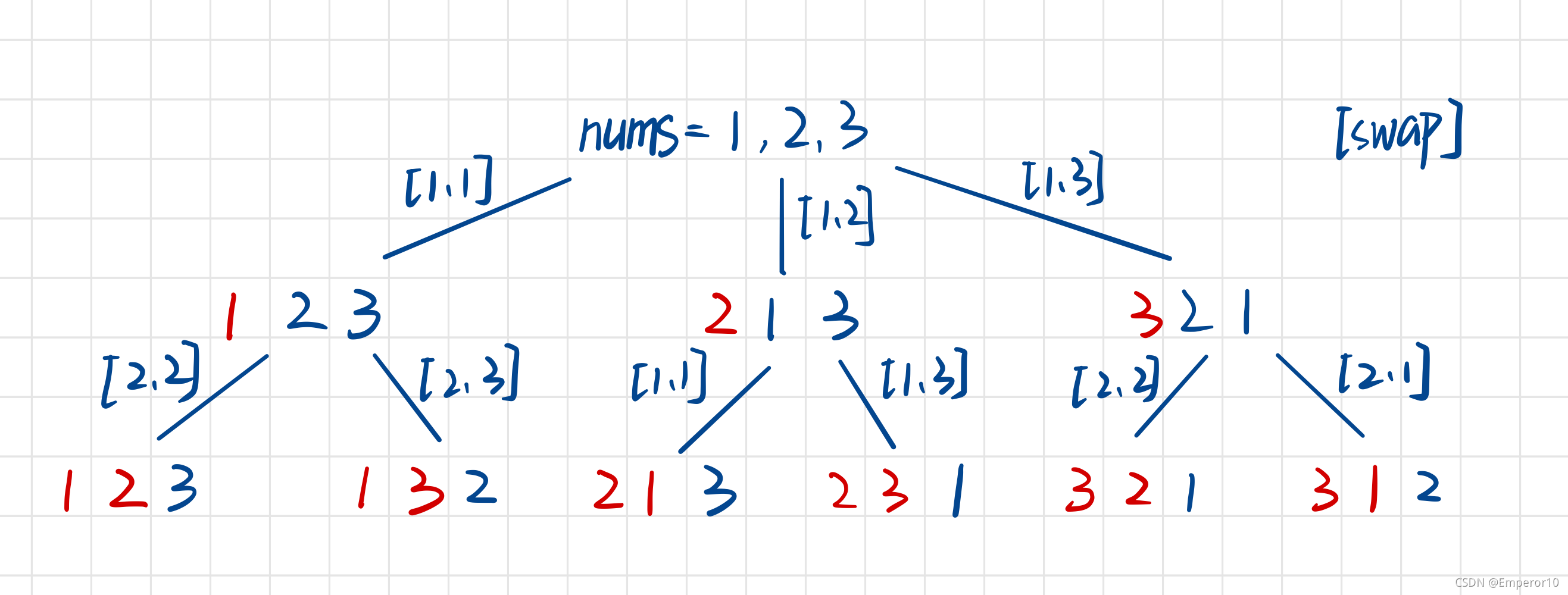
思路： 与字符串排列大同小异，不过需要注意的是，本题的输入是数组，那么 1>
存入list中时需要遍历数组一个一个元素存进去，没有字符串操作方便，本题单独定义了一个arraylist方法来添加。 2>
数组进行去重操作也没有字符串便捷，所以将两个列表转换为字符串比较。当然去重方法很多，也可以用双重for循环，HashSet等。

class Solution {
    public void swap(int[] nums,int x,int y){
        int temp = nums[x];
        nums[x] = nums[y];
        nums[y] = temp;
    }
    public void arraylist(int[] nums,List<Integer> list){
        for(int i = 0; i < nums.length; i++){
            list.add(nums[i]);
        }
    }
    public boolean isRepeat(List<List<Integer>> result,List<Integer> list){
        String s = result.toString();
        String l = list.toString();
        return s.contains(l);
    }
    public void DFS(int[] nums,int start,List<Integer> list,List<List<Integer>> result){
        if(start == nums.length-1){
            if(!isRepeat(result,list))
                result.add(new ArrayList<Integer> (list));
        }

        for (int i = start; i < nums.length; i++) {
            swap(nums,i,start);
            list.clear();
            arraylist(nums,list);
            DFS(nums,start+1,list,result);
            swap(nums,i,start);

        }
    }
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        if(nums.length == 0) return result;
        if(nums.length == 1) {
            list.add(nums[0]);
            result.add(list);
            return result;
        }
        DFS(nums,0,list,result);
        return result;
    }
}

2. 组合问题

给定N个数，按一定规则找出K个数的集合。与排列问题不同的是，组合问题结果集的长度不一定，只要满足规则，无论待选结果集中有几个元素都时可以加入结果集中的。
假设题目给定条件是找出{1,2,3}个数中和为3的数，那么最终返回的结果集应该是{{3},{1,2}}。注意{1,2}和{2,1}不是一个排列顺序，但却是一个集合，所以此处结果集中只能存在一个。

2.1 组合

leetcode：组合

注意：数组中没有重复元素；

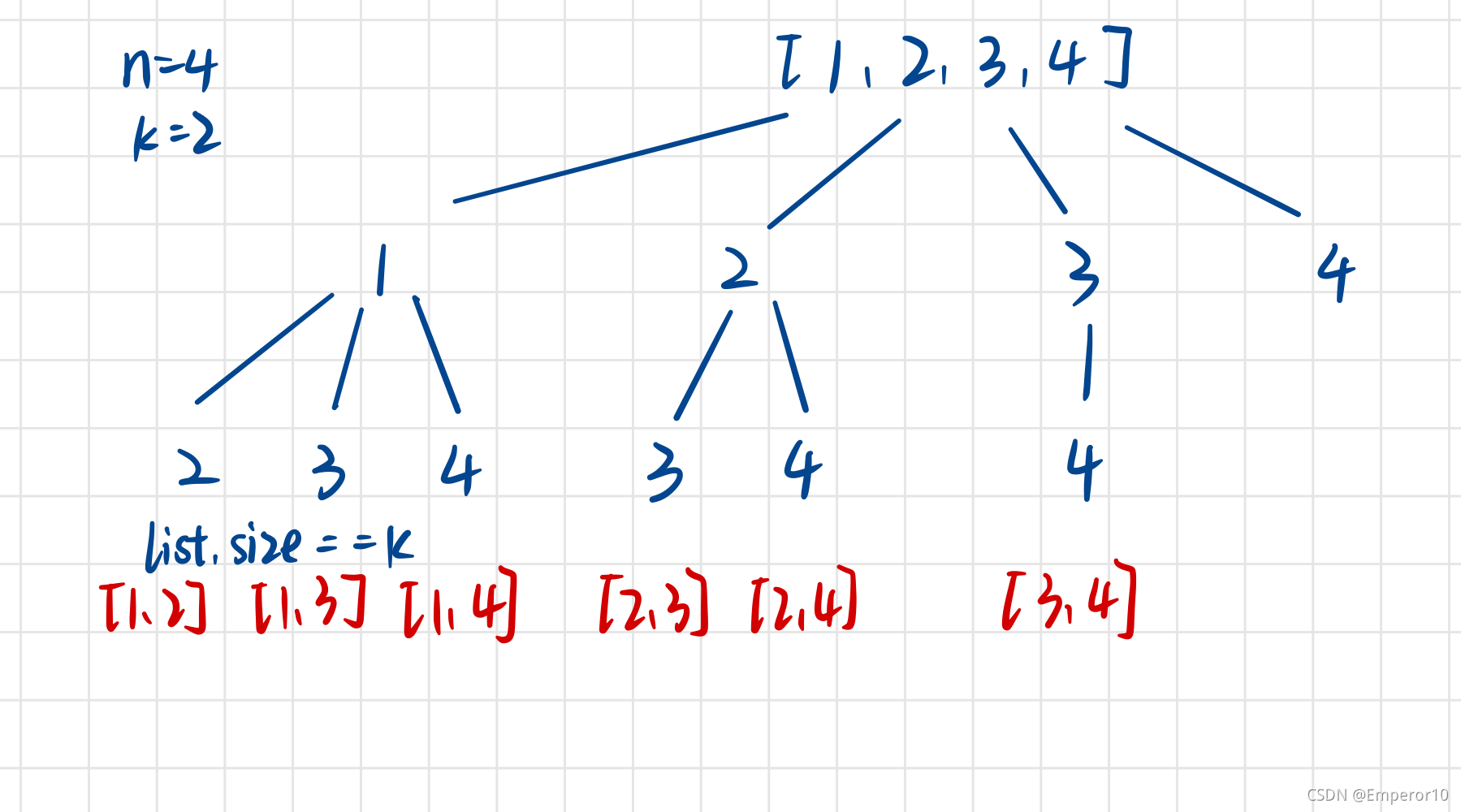
思路： 循环判断每一位数字，通过参数 start 来控制for循环的起始位置，达到缩小选择范围的作用，每一层的DFS都更新 start 下标。
递归终止条件就是待选结果集 list 的长度等于题目要求个数k；

在这里插入图片描述

class Solution {
    public void DFS(int start,int n,int k,List<Integer> list,List<List<Integer>> result){
        if(list.size() == k){
            result.add(new ArrayList<>(list));
            return;
        }
        for(int i = start; i <= n; i++){
            list.add(i);
            DFS(i+1,n,k,list,result);
            list.remove(list.size()-1);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        DFS(1,n,k,list,result);
        return result;
    }
}

2.2 组合总数Ⅲ

leetcode：组合总数Ⅲ

思路： 循环判断每一位数字，通过参数 start 来控制for循环的起始位置，达到缩小选择范围的作用，每一层的DFS都更新 start 下标。

单层的搜索中，循环添加元素后同时要更新target值，回溯时不仅要删掉list中的最后一个元素，同时也要将target值重置回去。
为了你面参数过多影响代码可读性，所以不设置sum来进行计算，与target比较判断。我们采用另外一种方式，每次添加一个元素，就用target的值减去添加的元素，直到target = 0时，说明添加的元素和正好等于target。
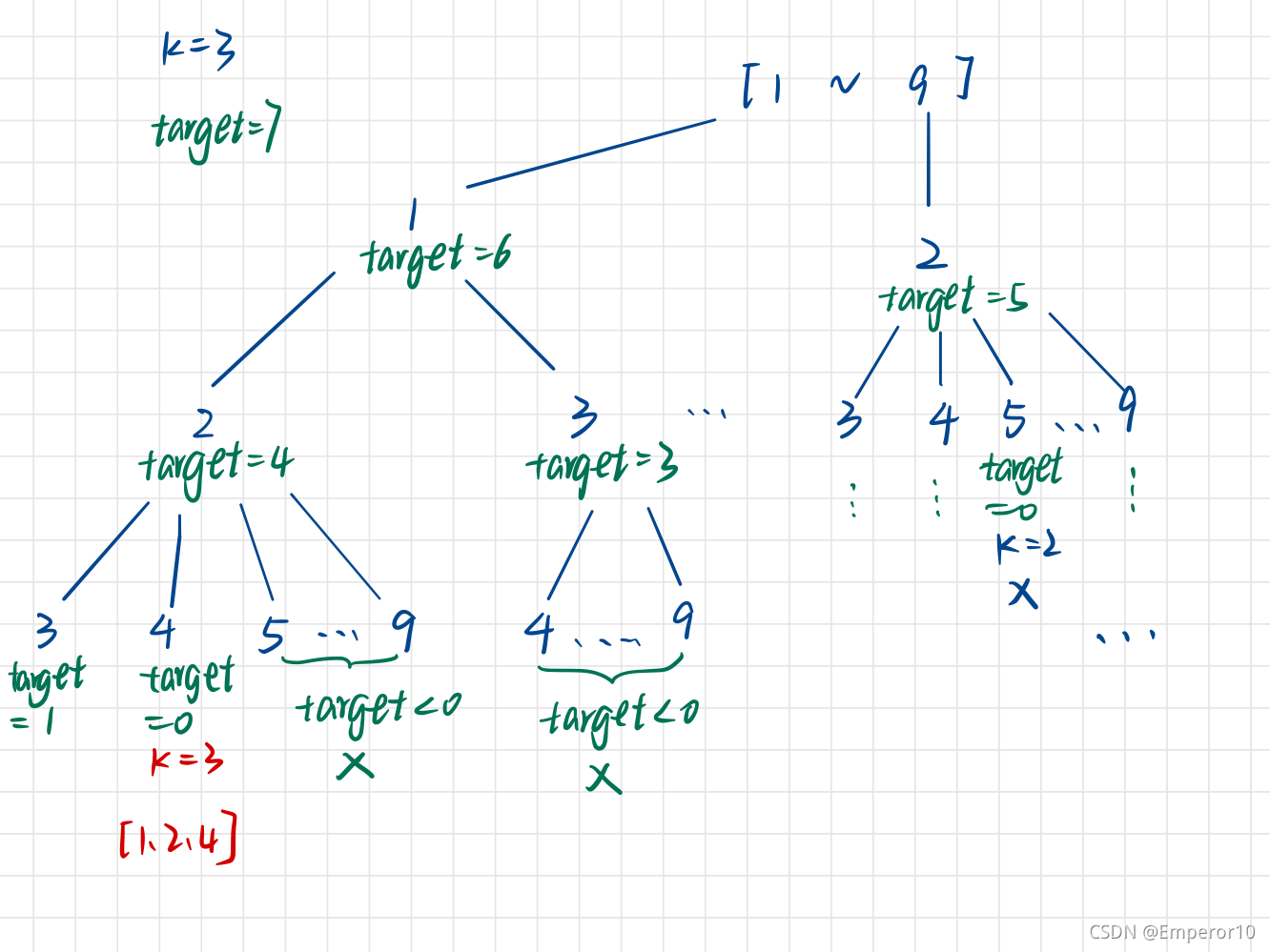
递归终止条件有两个：
1> 待选结果集 list 的长度等于题目要求个数k；
2> target == 0
3> 如图所示，当多叉树走到 target<0 的情况时就可以直接剪枝了。

在这里插入图片描述

class Solution {
    public void DFS(int start,int k,int target,List<Integer> list,List<List<Integer>> result){
        if(list.size() == k && target != 0){
            return;
        }
        if(target < 0) return;
        if(list.size() == k && target == 0){
            result.add(new ArrayList<>(list));
            return;
        }
        for(int i = start; i <= 9; i++){
            list.add(i);
            target = target - i;
            DFS(i+1,k,target,list,result);
            list.remove(list.size()-1); //回溯 删一个元素
            target = target + i; //回溯 同时target要重新加回去
        }
    }
    public List<List<Integer>> combinationSum3(int k, int target) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        if(k == 0 || target == 0) return result;
        DFS(1,k,target,list,result);
        return result;
    }
}

2.3 组合总数Ⅱ

leetcode：组合总数Ⅱ
注意：本题与1组合总数的区别在于，数组有重复元素，但还不能有重复的组合，本题的难点在于如果进行集合去重。
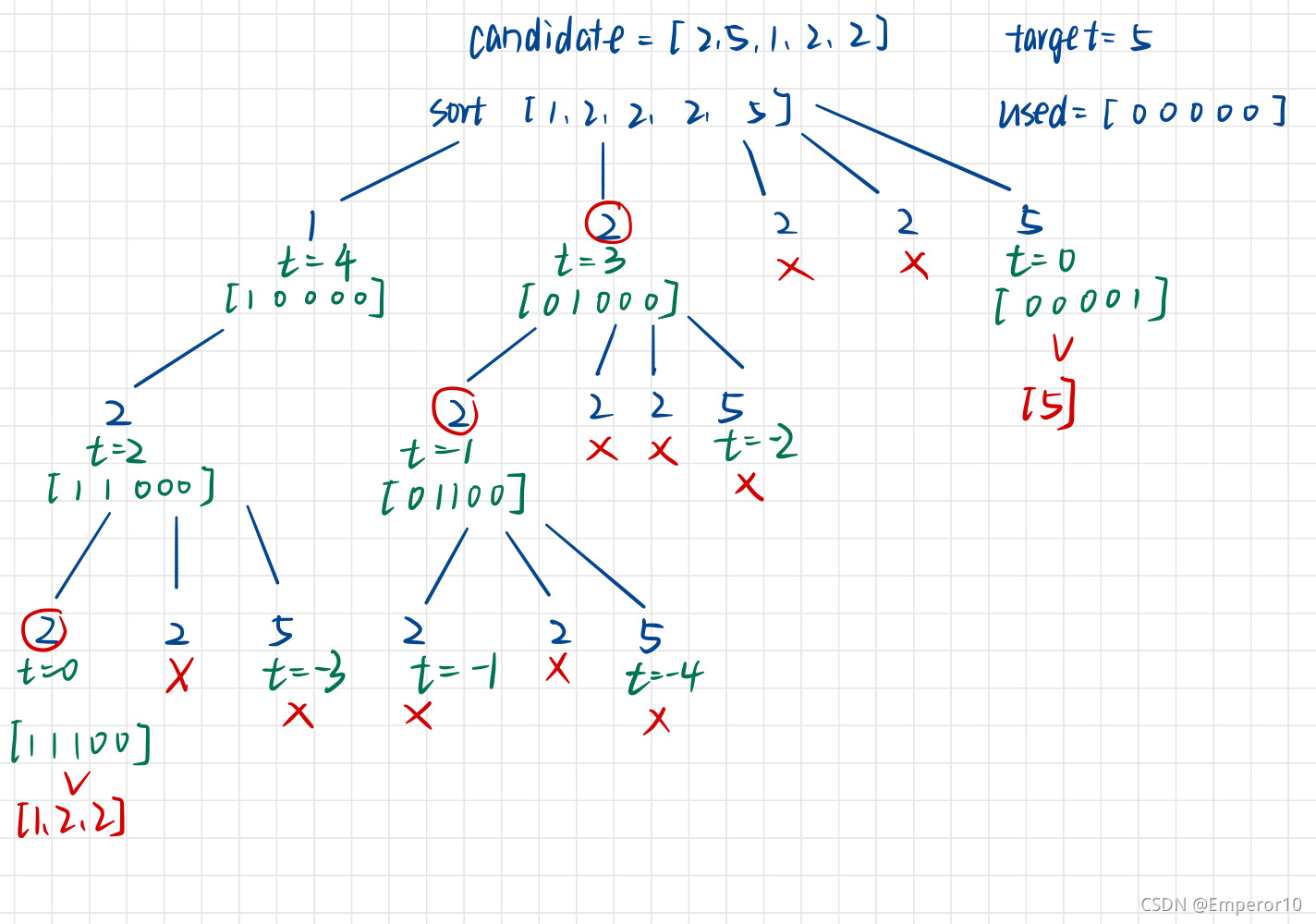
在这里插入图片描述

class Solution {
    public void DFS(int[] candidates,int target,int start,int[] used,List<Integer> list,List<List<Integer>> result){
        if(target < 0) return; //剪枝条件
        if(target == 0){
            result.add(new ArrayList<>(list)); 符合条件的解加入结果集
            return;
        }
        for(int i = start; i < candidates.length; i++){
            //去重，保证在递归树里面，同一层中一个元素只使用一次
             if(i>start && candidates[i]==candidates[i-1]){
                continue;
            }
            list.add(candidates[i]);
            target -= candidates[i];
            DFS(candidates,target,i+1,used,list,result); //下一个元素是i+1，因为要求元素不可以重复
            list.remove(list.size()-1);
            target += candidates[i];
        }
    }
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        int[] used = new int[candidates.length];
        if(candidates.length == 0 || target == 0) return result;
        Arrays.sort(candidates); //先排序，为去重做准备
        DFS(candidates,target,0,used,list,result);
        return result;
    }
}

2.4 电话号码的字母组合

leetcode：电话号码的字母组合

这道题与前面几道组合题最大的区别在于本题是不同集合求组合。细节较多，所以需要考虑如下问题：
1> 电话表中数字与字母的映射。可以定义一个字符串数组存储，要注意1和#这些特殊情况；
2> 递归终止条件：递归深度 start == 给定字符串长度digits.length;
3> 单层搜索逻辑?：首先要取 start 指向的数字phone_index，并找到对应的字符phone_s，再循环中遍历该字符串phone_s，同时对待选结果集 str 做添加和删除操作。

然后for循环来处理这个字符集，代码如下：

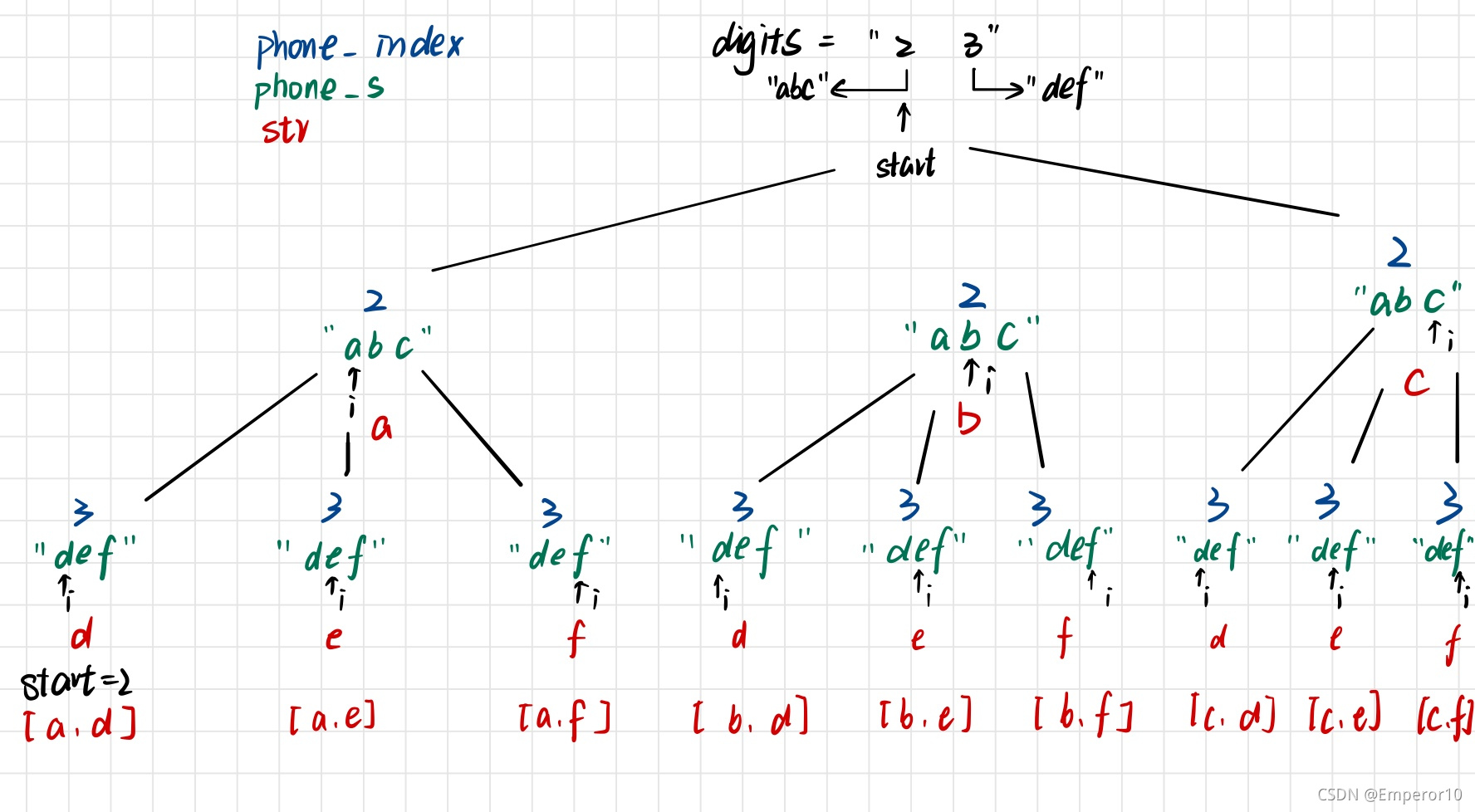
在这里插入图片描述

class Solution {
   //字母与数组的映射数组
    String[] phoneString = {"", "", "abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    //start指向digits的下标
    //i指向对应字符串abc的下标
    public void DFS(String digits,int start,StringBuilder str,List<String> result){
        //1. 退出递归条件
        if(start == digits.length()){
            result.add(str.toString());
            return;
        }
        //找到当前字符在 phone 电话号码 映射表中对应的字符串
        int phone_x = digits.charAt(start) - '0';
        String index = phoneString[phone_x];
        //2. 尝试当下的每一种可能 / 剪枝
        for(int i = 0; i < index.length(); i++) {
            str.append(index.charAt(i));
            //3. 下一层DFS
            DFS(digits,start+1,str,result);
            //4. 回溯
            str.deleteCharAt(str.length()-1);
        }
    }
    public List<String> letterCombinations(String digits) {
        List<String> result = new ArrayList<>(); //结果集
        StringBuilder str = new StringBuilder(""); //待选结果集
        if(digits.length() == 0) return result;
        DFS(digits,0,str,result);
        return result;
    }
}

3. 棋盘问题

我们知道二叉树的回溯问题需要递归判断其左右子树，排列组合等多叉树的问题需要根据题目条件具体判断是几叉树，而棋盘问题其相邻节点一定是某个点的上下左右四个方向的点，另外再考虑一下是否越界的问题，同时为了避免重复搜索，通常情况下棋盘问题都会定义一个标记数组。
总的来说这部分题型非常单一，比较容易。

3.1 图像渲染

leetcode：图像渲染

思路： 先将起始位置显渲染，判断起始位置的上下左右四个格子，同时判断新位置的合法性，避免出现数组越界的情况；如果新位置符合条件，即没有被渲染并且没有被标记过，那么将该位置作为新的起始位置，重复操作。

class Solution {
    //4*2的方向数组，每一行表示四个不同方向，两列代表行列
    int[][] position = {{0,-1},{1,0},{0,1},{-1,0}}; 
    public void DFS(int[][] image,int row,int col,int sr,int sc,int[][] book,int oldColor,int newColor){
        image[sr][sc] = newColor;
        book[sr][sc] = 1;
        for(int i = 0; i < 4; i++){ //判断当前位置的上下左右四个方向
            int new_sr = sr + position[i][0];
            int new_sc = sc + position[i][1];
            if(new_sr >= row || new_sr < 0 || new_sc >= col || new_sc < 0){ //新坐标范围不合法
                continue;
            }
            //新坐标点颜色newColor==目标点颜色oldColor && 新坐标点没有被标记过
            if(image[new_sr][new_sc] == oldColor && book[new_sr][new_sc] == 0){
                DFS(image,row,col,new_sr,new_sc,book,oldColor,newColor); //就向新坐标渲染，即下一层DFS
            }
        }
    }
    public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
        int row = image.length;
        int col = image[0].length;
        int oldColor = image[sr][sc];
        int[][] book = new int[row][col];
        DFS(image,row,col,sr,sc,book,oldColor,newColor);
        return image;
    }
}

3.2 岛屿的周长

leetcode：岛屿的周长

思路： 先找到任意一个陆地，即格子[1]，将该位置作为起始位置传入DFS，同时标记访问过的格子，遍历其上下左右方向的格子，只要为0，就周长result++；若是位置不合法，说明是边界，根据题目要求，同样周长result++；若是为1，并且没有被标记过，就将此位置作为新的起始位置重复操作。

class Solution {
    public int result = 0;
    int[][] position = {{0,-1},{1,0},{0,1},{-1,0}}; 
    public void DFS(int[][] grid,int row,int col,int sr,int sc,int[][] book){
        book[sr][sc] = 2;
        //访问4个相邻节点上下左右
        for(int i = 0; i < 4; i++){
            int new_sr = sr + position[i][0];
            int new_sc = sc + position[i][1];
            //如果新坐标越界,说明是边界,result++
            if(new_sr >= row || new_sc >= col || new_sr < 0 || new_sc < 0){
                result++;
                continue;
            }
            //如果新坐标是水域,那么result++;
            if(grid[new_sr][new_sc] == 0){
                result++;
                continue;
            }
            //如果新坐标也是岛屿1,那么DFS
            if(grid[new_sr][new_sc] == 1 && book[new_sr][new_sc] != 2){
                DFS(grid,row,col,new_sr,new_sc,book);
            }
        }
    }
    public int islandPerimeter(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int sr = 0,sc = 0; //当前坐标
        int[][] book = new int[row][col]; //标记数组
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if(grid[i][j] == 1){
                    sr = i;
                    sc = j;
                    break;
                }
            }
        }//此时[sr,sc]为起始坐标格子1
        DFS(grid,row,col,sr,sc,book);
        return result;
    }
}

3.3 被围绕的区域

leetcode：被围绕的区域

思路： 题目要求将被X围绕的O换掉，想要单独找出被围绕的区域不太容易。我们可以换个思路，去找所有与边界联通的O，将这些不满足要求的O替换成A，最后循环遍历一遍整个数组，此时数组中的O全是被围绕的O，将所有的O换成X，再将原来与边界联通的O换回来即可。

class Solution {
    int[][] position = {{0,-1},{1,0},{0,1},{-1,0}}; //顺时针旋转
    //传入DFS中的当前坐标一定是边界O
    public void DFS(char[][] board,int row,int col,int sr,int sc){
        board[sr][sc] = 'A';
        for(int i = 0; i < 4; i++){
            int new_sr = sr + position[i][0];
            int new_sc = sc + position[i][1];
            //新坐标越界
            if(new_sr>=row || new_sc>=col || new_sr<0 || new_sc<0){
                continue;
            }
            //因为遍历过的'O'会被修改为'A',相当于实现了标记，所以不用再设一个标记数组
            if(board[new_sr][new_sc]=='O'){
                DFS(board,row,col,new_sr,new_sc);
            }
        }
    }
    public void solve(char[][] board) {
        int row = board.length;
        int col = board[0].length;
        //寻找边界位置
        //查找第一行和最后一行
        for(int j = 0; j < col; j++){
            if(board[0][j] == 'O')
                DFS(board,row,col,0,j); //起始位置:board[0][j]
            if(board[row-1][j] == 'O')
                DFS(board,row,col,row-1,j); //起始位置:board[row-1][j]
        }
        //查找第一列和最后一列
        for(int i = 0; i < row; i++){
            if(board[i][0] == 'O')
                DFS(board,row,col,i,0); //起始位置:board[i][0]
            if(board[i][col-1] == 'O')
                DFS(board,row,col,i,col-1); //起始位置:board[i][col-1]
        }
        /**
         * 整体遍历数组
         * 1. 格子为'O',置为'X';
         * 2. 格子为'A',置为'O';
         * 3. 格子为'X',不做操作;
         */
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if(board[i][j] == 'O')
                    board[i][j] = 'X';
                if(board[i][j] == 'A')
                    board[i][j] = 'O';
            }
        }//for
    }
}

3.4 岛屿数量

leetcode：岛屿数量

思路： 本题与[岛屿周长]方法类似，先找到棋盘中任意一个值为1的格子[1]，更新记录数量的result，同样的访问过的格子要标记，判断该点的上下左右四个方向，如果新位置合法，同时是陆地（值为1的格子），且没有被标记过，那么将新位置作为起始位置重复操作。

class Solution {
    int[][] position = {{0,-1},{1,0},{0,1},{-1,0}}; //顺从时针旋转
    public void DFS(char[][] grid,int row,int col,int sr,int sc,int[][] book){
        book[sr][sc] = 2;
        //当前坐标grid[sr][sc]一定为1
        for(int i = 0; i < 4; i++){
            int new_sr = sr + position[i][0];
            int new_sc = sc + position[i][1];
            if(new_sr >= row || new_sc >= col || new_sr < 0 || new_sc < 0){
                continue;
            }
            if(grid[new_sr][new_sc]=='1' && book[new_sr][new_sc]==0){
                DFS(grid,row,col,new_sr,new_sc,book);
            }
        }
    }
    public int numIslands(char[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int result = 0;
        int[][] book = new int[row][col];
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if(grid[i][j] == '1' && book[i][j] == 0){
                    result++;
                    DFS(grid,row,col,i,j,book);
                }
            }
        }
        return result;
    }
}

3.5 岛屿的最大面积

leetcode：岛屿的最大面积

思路： 循环遍历数组，找到格子1，传入DFS中判断上下左右方向，判断新坐标合法性，判断是否被访问过，整个递归结束表示一个岛屿已经找完，其数量用result存储，同样的操作继续计算下一片岛屿的数量，如果比result大，就替换result，那么最后整个数组遍历完，result中存放的就是最大岛屿的数量。

class Solution {
    int[][] position = {{0,-1},{1,0},{0,1},{-1,0}};
    public int DFS(int[][] grid,int row,int col,int sr,int sc,int[][] book){
        book[sr][sc] = 2;
        int area = 1;
        for(int i = 0;i < 4; i++){
            int new_sr = sr + position[i][0];
            int new_sc = sc + position[i][1];
            if(new_sr>=row || new_sc>=col || new_sr<0 || new_sc<0){
                continue;
            }
            if(grid[new_sr][new_sc] == 1 && book[new_sr][new_sc] == 0){
                area += DFS(grid,row,col,new_sr,new_sc,book);
            }
        }
        return area;
    }
    public int maxAreaOfIsland(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[][] book = new int[row][col];
        int result = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if(grid[i][j] == 1 && book[i][j] == 0){
                     int area = DFS(grid,row,col,i,j,book);
                     result = Math.max(result, area);
                }
            }
        }//for
        return result;
    }
}