红黑树条件????????

根为黑
红结点的子结点黑
对于每个结点，从该结点到后代叶子的所有简单路径都包含相同数量的黑色结点

结点定义

typedef struct RBTnode
{
	int data;
	bool color; // 0 for black, 1 for red
	RBTnode *lchild, *rchild;
	int left, right, it;
} * RBTree, Node, *node;

判断方式

判断根的颜色是否为黑
判断红结点的子结点颜色
1. 通过任意顺序遍历一次，如果是红色，就判断子结点是否为黑色
判断任意结点到所有后代叶子是否包含相同数量的黑色结点
1. 结构:
  对于每一个结点，加入三个数据:
  1. left:从左子到叶有多少个黑结点
  2. right:从右子到叶有多少个黑结点
  3. it:自己到叶有多少个黑结点
2. 例子:
  以该树为例
  ??
  
  对于结点4
  
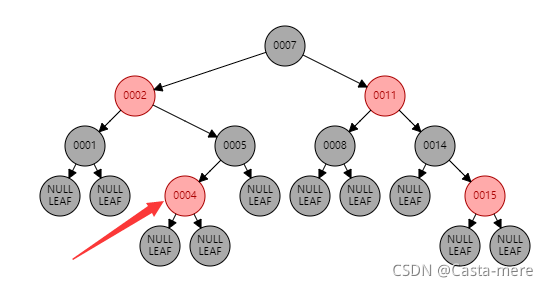
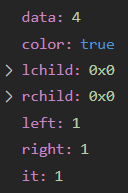
  左右子树到叶均有一个黑(left，right为1)
  
  自己为红(it等于left或right等于1)
  
  对于结点5
  
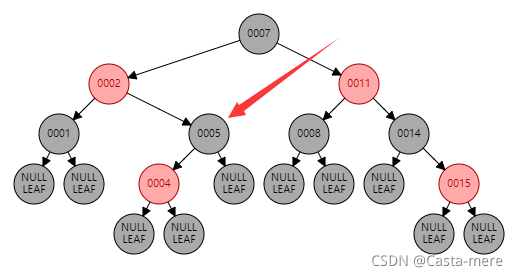
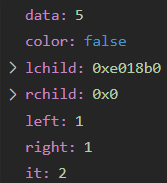
  左右子树到叶均有一个黑(left，right为1)
  
  自己为黑(it等于left或right加一，等于2)
  
  对于结点1
  
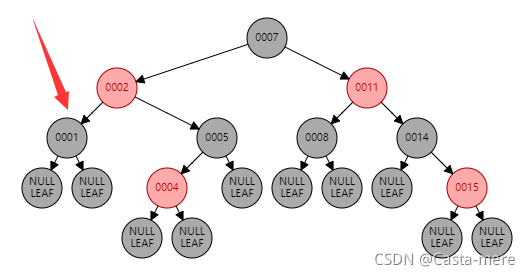
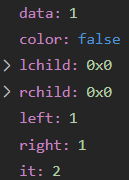
  左右子树到叶均有一个黑(left，right为1)
  
  自己为黑(it等于left或right加一，等于2)
  
  对于结点2
  
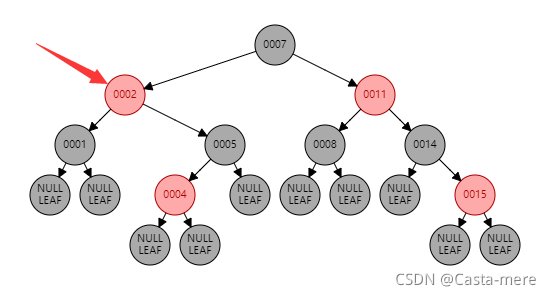
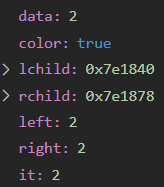
  左右子树到叶均有两个黑(left，right为2)
  
  自己为红(it等于left或right等于2)
?规律
1. 每一个结点如果有左子树，那么他的的left等于他lchild的it，如果没有左子树，那么他的left等于1(NULL为黑)
  每一个结点如果有右子树，那么他的的right等于他rchild的it，如果没有右子树，那么他的right等于1(NULL为黑)
2. 如果一个结点的left和right相等
  ? ? ? ?每一个红结点的it等于他的left或right
  ? ? ? ?每一个黑节点的it等于他的(left或right)+1
  如果一个结点的left和right不相等
  ? ? ? ?说明不是红黑树
3. 由1)和2)可以发现，在处理每一个结点的时候，需要先了解他的lchild，rchild的情况，也就是处理顺序为子->父，按照什么顺序能刚好把一棵树按照子->父的顺序遍历一遍呢，刚好是后序(左右根)。

综上所述，只需要先判断根是否为黑，再后序遍历一遍，即可判断是否为红黑树

实现

void No()
{
    system("cls");
    printf("No\n");
    exit(0);
}

void judge(node x)
{
    if (x->color) //根为红
        No();
    post_order_t(x);
    system("cls");
    printf("Yes\n");
}

void post_order_t(node x)
{
    if (!x)
        return;
    post_order_t(x->lchild);//左
    post_order_t(x->rchild);//右

    //判断红色节点的子节点是否为黑
    if (x->color)
    {
        if (x->rchild)
            if (x->rchild->color)
                No();
        if (x->lchild)
            if (x->lchild->color)
                No();
    }

    //判断左右有几黑
    if (x->lchild)
        x->left = (x->lchild->it);
    else
        x->left = 1;
    if (x->rchild)
        x->right = (x->rchild->it);
    else
        x->right = 1;
    if (x->left == x->right)
        x->it += x->left;
    else
        No();
}

经验总结

首先要搞清楚，一共要判断哪些东西，比如，该题要先判断红结点的子结点颜色，可以用任意顺序遍历，但不用着急写实现。另一个在判断内容后，发现需要后序遍历，都研究好之后，可以用一次后序遍历处理掉所有问题。

其次是善于运用bool型变量，将1和0与实际需求联系起来，比如在判断红结点的子节点是否为黑时，更多需要的是判断某个结点是否为红

//判断红色节点的子节点是否为黑
if (x->color)
{
    if (x->rchild)
        if (x->rchild->color)
            No();
    if (x->lchild)
        if (x->lchild->color)
            No();
}

此时，1代表红，0代表黑就可以很好的利用起来