[数据结构与算法]剑指offer——第二十三天(数学)

第一题：剑指 Offer 14- I. 剪绳子

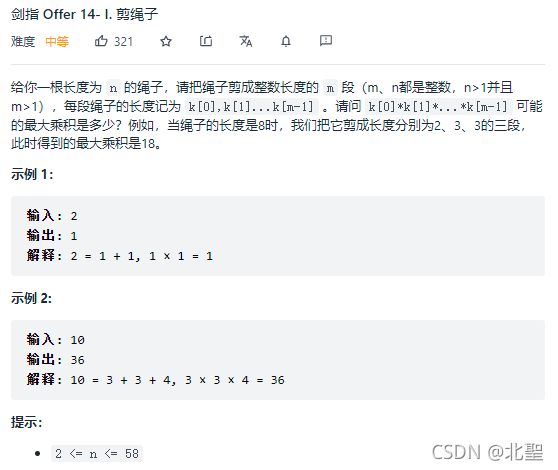
问题描述

思路

剪绳子用数学公式可以得到最大长度剪成3，其次是2；
当绳子长度小于3时，需要自己判断。也就只能分两段。
所以一段绳子的长度就可以用3来进行划分思路在代码中清楚体现，大家可以看看。

代码

class Solution {
    public int cuttingRope(int n) {
        if(n<=3) return n-1;
        int a = n / 3;
        int b = n % 3;
        if(b == 0) return (int)Math.pow(3,a);
        if(b == 1) return (int)Math.pow(3,a-1)*4;
        else return (int)Math.pow(3,a)*2;
    }
}

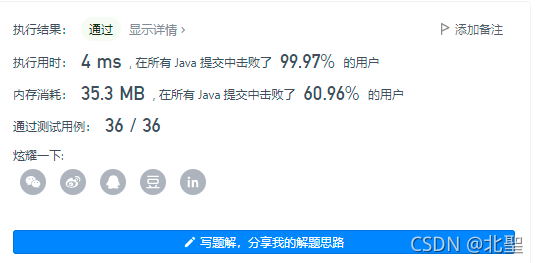
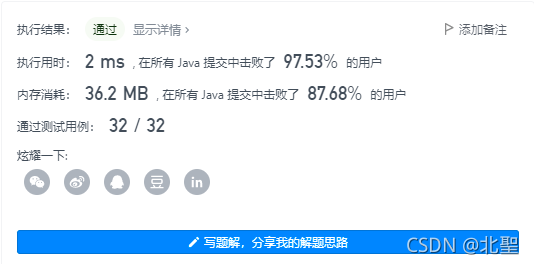
时间空间复杂度

第二题：剑指 Offer 57 - II. 和为s的连续正数序列

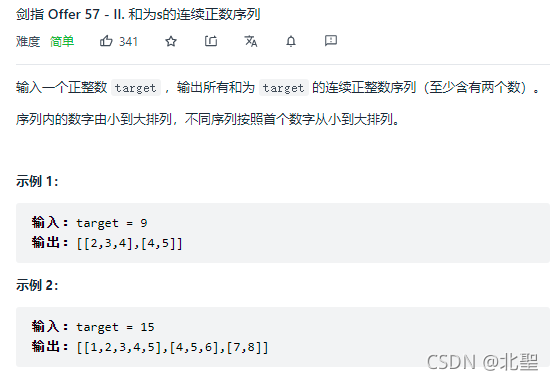
问题描述

思路一：滑动窗口（个人觉得比官方给的数学的方法好理解）

一串数字连续的，因此求能满足目标值得一串数字也就是相领的几个数字，可以用滑动窗口来表示，如果值小于目标值窗口右边就向右移动，大于的话，窗口左边向右移动找满足的值。

代码

class Solution {
    public int[][] findContinuousSequence(int target) {
        List <int[]> list = new ArrayList<>();       
        for(int left=1,right=1,sum=0;right<target;right++){         
            sum += right;
            while(sum > target){
                sum -= left;
                left++;
            } 
            if(sum == target){
                int array[] = new int[right-left+1];
                for(int i=0;i < array.length;i++){
                    array[i] = left+i;                    
                }
                list.add(array);
            }
        }
        int res [][] = new int[list.size()][];
        for(int i=0;i<res.length;i++){
            res[i] = list.get(i);
        }
        return res;
    }
}

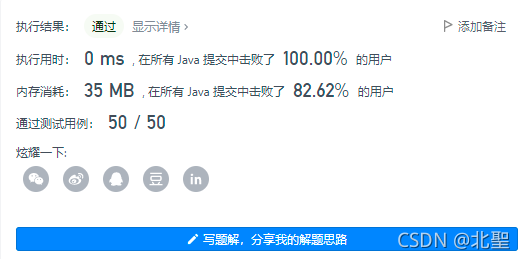
时间空间复杂度

思路二：数学思想（博主理解有点难）

博主自己理解有点困难，发代码出来让大家可以看看，毕竟是数学的思路和方法。

代码

class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> vec = new ArrayList<int[]>();
        int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
        for (int x = 1; x <= limit; ++x) {
            long delta = 1 - 4 * (x - (long) x * x - 2 * target);
            if (delta < 0) {
                continue;
            }
            int delta_sqrt = (int) Math.sqrt(delta + 0.5);
            if ((long) delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1) % 2 == 0) {
                int y = (-1 + delta_sqrt) / 2; // 另一个解(-1-delta_sqrt)/2必然小于0，不用考虑
                if (x < y) {
                    int[] res = new int[y - x + 1];
                    for (int i = x; i <= y; ++i) {
                        res[i - x] = i;
                    }
                    vec.add(res);
                }
            }
        }
        return vec.toArray(new int[vec.size()][]);
    }
}

时间空间复杂度

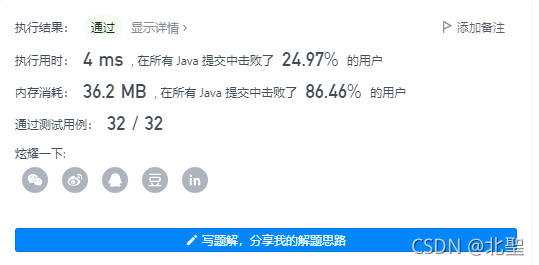
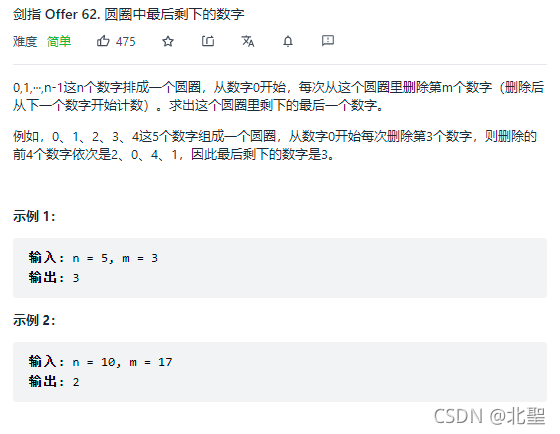
第三题：剑指 Offer 62. 圆圈中最后剩下的数字

问题描述

思路

约瑟夫环，用倒推法；

代码

class Solution {
    public int lastRemaining(int n, int m) {
        int x = 0;
        for(int i=2;i<=n;i++){
            x = (x+m) % i;
        }
        return x;
    }
}

时间空间复杂度