贪心算法总结
1.活动安排问题
问题描述
设有n个活动的集合 E = {1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动 i 都有一个要求使用该资源的起始时间 si 和一个结束时间 fi,且 si < fi。如果选择了活动 i,则它在半开时间区间 [si, fi) 内占用资源。若区间 [si, fi) 与区间 [sj, fj) 不相交,则称活动 i 与活动 j 是相容的。也就是说,当 si ≥ fj 或 sj ≥ fi 时,活动 i 与活动 j 相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。
基本思想
将活动按照结束时间进行从小到大排序。然后用 i 代表第 i 个活动,s[i] 代表第 i 个活动开始时间,f[i] 代表第 i 个活动的结束时间。挑选出结束时间尽量早的活动(活动结束时间最早的活动),并且满足后一个活动的起始时间晚于前一个活动的结束时间,全部找出这些活动就是最大的相容活动子集合。即有活动 i,j 为 i 的下一个活动。f[i]最小,s[j] >= f[i]。
证明贪心策略
证明:设 E ={0,1,2,…,n-1}为所给的活动集合。由于 E 中活动安排安结束时间的非减序排列,所以活动 1 具有最早完成时间。首先证明活动安排问题有一个最优解以贪心选择开始(选择了活动 1)。设 A 是所给的活动安排问题的一个最优解,且 B 中活动也按结束时间非减序排列,A 中的第一个活动是活动 k。若 k = 1,则 A 就是一个以贪心选择开始的最优解。若 k > 1,则我们设 B = A -{k}∪{1}。由于 end[1] ≤ end[k](非减序排列),且 A 中活动是互为相容的,故 B 中的活动也是互为相容的。又由于 B 中的活动个数与 A 中活动个数相同,且 A 是最优的,故 B 也是最优的。也就是说 B 是一个以贪心选择活动 1 开始的最优活动安排。因此,证明了总存在一个以贪心选择开始的最优活动安排方案,也就是算法具有贪心选择性质。
代码如下
#include <iostream>
#include <algorithm>
using namespace std;
const int N=100;
pair <int,int> p[N];
int main(){
int n;
cin >>n;
for(int i=0;i<n;i++){
cin >> p[i].second>> p[i].first;
}
sort(p,p+n);
pair<int,int>p1;
p1=p[0];
int max=1 ;
for(int i=1;i<n;i++){
if(p[i].second>=p1.first){
max++;
p1=p[i];
}
}
cout << max;
}
2.哈夫曼编码
问题描述
哈夫曼编码是广泛用于数据文件压缩的十分有效的编码方法。其压缩率通常为20%~90%。哈夫曼编码算法使用字符在文件中出现的频率表来建立一一个用0、1串表示各字符的最优表示方式。假设有一个数据文件包含100000个字符,要用压缩的方式存储它。该文件中各字符出现的频率如表4-1所示。文件中共有6个不同字符出现,字符a出现45000次,字符b出现13000次等。
有多种方法表示文件中的信息。考察用0、1 码串表示字符的方法,即每个字符用唯一的一个0、1串表示。若使用定长码,则表示6个不同的字符需要3位: a=000 b=001,……,f=101.用这种方法对整个文件进行编码需要300000位。能否做得更好些呢?使用变长码要比使用定长码好得多。给出现频率高的字符较短的编码,出现频率较低的字符以较长的编码,可以大大缩短总码长。表4-1给出了一种变长码编码方案。其中,字符a用一位串0表示,而字符f用4位串1100表示。用这种编码方案,整个文件的总码长为(45x1+13x3+12x3+16x3+9x4+5x4)*1000=224000位,比用定长码方案好,总码长减小约25%。事实上,这是该文件的最优编码方案。
图示生成哈夫曼树的过程:
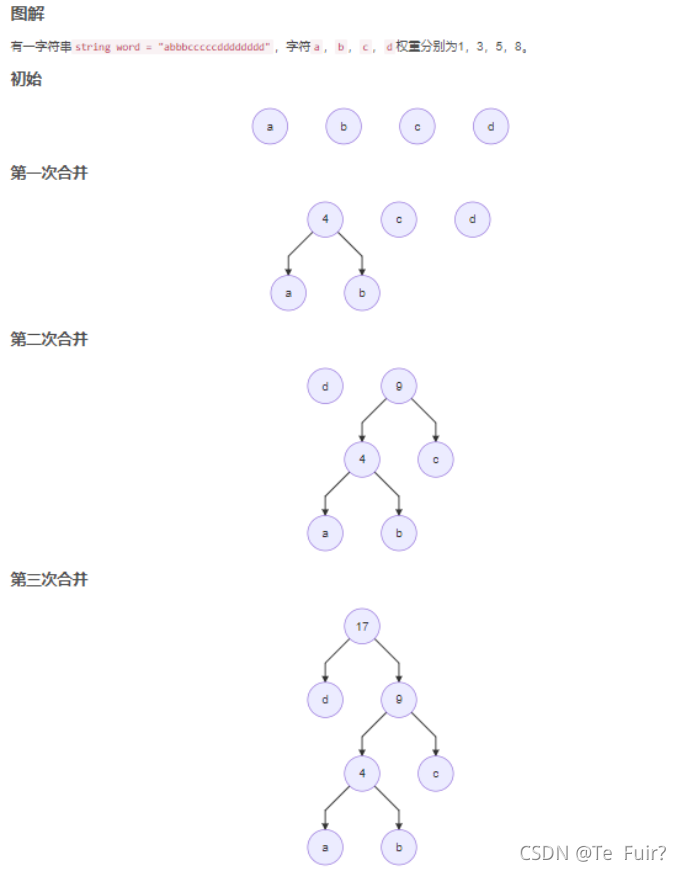
可以创建一个最小堆来维护权值最小的数,时间复杂度为nlogn,如果每次选出最小值,对其·排序,时间复杂度就是排序的时间复杂度。
代码如下:
#include <iostream>
#include <map>
#include <queue>
using namespace std;
const int N=100;
pair<int ,char>p[N];
struct Node
{
int weight;
char ch = ' ';
string code;
Node *left = NULL;
Node *right = NULL;
};
class cmp
{
public:
bool operator()(const Node *a, const Node *b)
{
return a->weight > b->weight;
}
};
Node *Huffman(priority_queue<Node *, vector<Node *>, cmp> *H)
{
Node *T;
int times = H->size();
for (int i = 1; i < times; i++)
{
T = new Node;
T->left = H->top();
H->pop();
T->right = H->top();
H->pop();
T->weight = T->left->weight + T->right->weight;
H->push(T);
}
return H->top();
}
void qianxu(Node *Huff)
{
if (Huff)
{
if (Huff->ch != ' ')
{
cout << Huff->ch << " " << Huff->weight << " " << Huff->code << endl;
}
qianxu(Huff->left);
qianxu(Huff->right);
}
}
//左子树加0,右子树加1
void GetCode(Node *Huff, string code)
{
if (Huff)
{
Huff->code = code;
GetCode(Huff->left, code + "0");
GetCode(Huff->right, code + "1");
}
}
int main()
{
int n;
cin >> n;
vector <Node *> vec;
int x;
char y;
for(int i=0;i<n;i++){
cin >> y >> x;
Node *N=new Node;
N->ch=y;
N->weight=x;
vec.push_back(N);
}
priority_queue<Node *, vector<Node *>, cmp> MinHeap(vec.begin(),vec.end());
Node *Tree = Huffman(&MinHeap);
GetCode(Tree, "");
cout << "Char Weight Code" << endl;
qianxu(Tree);
return 0;
}
3.单源最短路经(Dijkstra算法)
问题描述
给定一个 nn 个点 mm 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 11 号点到 nn 号点的最短距离,如果无法从 11 号点走到 nn 号点,则输出 ?1?1。
输入格式
第一行包含整数 nn 和 mm。
接下来 mm 行每行包含三个整数 x,y,zx,y,z,表示存在一条从点 xx 到点 yy 的有向边,边长为 zz。
输出格式
输出一个整数,表示 11 号点到 nn 号点的最短距离。
如果路径不存在,则输出 ?1?1。
数据范围
1≤n≤5001≤n≤500,
1≤m≤1051≤m≤105,
图中涉及边长均不超过10000。
算法思想(朴素版):首先使用邻接矩阵存储图中一个点到另一个点的权值,贪心的基本思想是即进行n(n为n的个数)次迭代去确定每个点到起点的最小值 最后输出的终点的即为我们要找的最短路的距离。适用于稠密图。
使用邻接矩阵存储时间复杂度为n的平方。
代码如下:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int a[N][N];
int d[N];
bool st[N];
int n,m;
int Dijkstra(){
memset(d ,0x3f,sizeof d);
d[1]=0;
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||d[t]>d[j]))t=j;
}
st[t]=true;
for(int j=1;j<=n;j++){
d[j]=min(d[j],d[t]+a[t][j]);
}
}
if(d[n]==0x3f3f3f3f) return -1;
return d[n];
}
int main(){
cin >> n >> m;
memset(a,0x3f,sizeof a);
while (m -- ){
int x,y,z;
cin >> x >> y >> z;
a[x][y]=min(a[x][y],z); //可能有两条不同的路径
}
cout << Dijkstra();
return 0;
}
堆优化版dijkstra(解决稀疏图)时间复杂度O(mlogn),n表示点数,m表示边数。

代码如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
vector<vector<pair<int, int>>> gra;
int dist[N];
int st[N];
int n, m;
int solve()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({ 0, 1 });
while (heap.size()) {
auto t = heap.top();
heap.pop();
int node = t.second; int distance = t.first;
if (st[node]) continue;
st[node] = true;
for (int i = 0; i < gra[node].size(); i++) {
int newnode = gra[node][i].first;
int len = gra[node][i].second;
if (dist[newnode] > dist[node] + len) {
dist[newnode] = dist[node] + len;
heap.push({ dist[newnode],newnode });
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d %d",&n,&m);
gra.resize(n + 1);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d %d %d",&a,&b,&c);
gra[a].push_back({ b,c });
}
printf("%d\n", solve() );
return 0;
}
4.会场安排问题
问题描述:假设要在足够多的会场里安排一批活动,并希望使用尽可能少的会场。设计一个有效的贪心算法进行安排(这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个顶点,不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数,相应于要找的最小会场数)。
算法设计:对于给定的k个待安排的活动,计算使用最少会场的时间表。
数据输入:第一行有一个正整数k,表示k个待安排的活动,接下来k行,每行有两个正整数,分别表示开始时间和结束时间。
结果输出:计算出最小的会场数。
输入实例:
5
1 23
12 28
25 35
27 80
36 50
输出实例:
3
算法思想:首先先按活动的起始时间排序,贪心选择性质为从被安排的会场中选择出一个,然后向后遍历,如果后面的起始时间大于前一个的结束时间,那么这两场安排在同一个会场,直到所有的会场安排完毕。
代码如下:
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
const int N=1000;
pair <int ,int>p[N];
struct node{
int a;
int b;
int flag;
}s[N];
int main(){
int k;
cin >> k;
for(int i=0;i<k;i++){
cin >> p[i].first >>p[i].second;
}
sort(p,p+k);
for(int i=0;i<k;i++){
s[i].a=p[i].first;
s[i].b=p[i].second;
s[i].flag=0;
}
int count=k;
int sum=0;
for(int i=0;i<k-1;i++){
if(s[i].flag==0){
sum++;
s[i].flag=1;
struct node s1;
s1=s[i];
for(int j=i+1;j<k;j++){
if(s[j].a>s1.b&&s[j].flag==0){
s1=s[j];
s[j].flag=1;
}
}
}
}
cout <<sum;
}
5.区间覆盖问题
问题描述:设x,x2,.xn是实直线上的n个点.用固定长度的闭区间覆盖这n个点,至少需要多少个这样的固定长度闭区间?设计解此问题的有效算法,并证明算法的正确性.
算法设计:对于给定的实直线上的n个点和闭区间的长度k,计算覆盖点集的最少区间数.
数据输入:第1行有2个正整数n和k,表示有n个点,且固定长度闭区间的长度为k。接下来的1行中有n个整数,表示n个点在实直线上的坐标(可能相同)。
结果输出:输出最少区间数.
输入实例:
7 3
1 2 3 4 5 -2 6
输出实例:
3
**算法思想:**先将输入的点排序,然后从最左边的点开始加线段,覆盖一部分点之后,从新的节点再加线段,直到所有的点都被覆盖为止。
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int n,k;
cin >> n>>k;
int a[n];
for(int i=0;i<n;i++){
cin >> a[i];
}
sort(a,a+n);
int sum=1;
for(int i=0;i<n;i++){
int t=a[i];
for(int j=i;j<n;j++){
if(a[j]-t>k){
sum++;
i=j-1;
break;
}
}
}
cout << sum;
}
6.删数问题
问题描述:给定n位正整数a,去掉其中任意k≤n个数字后,剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数a和正整数k,设计一个算法找出剩下数字组成的新数最小的删除方案。
算法设计:对于给定的正整数a,计算删去k个数字后得到的最小数。
数据输入:文件第一行是1个正整数a。第2行是正整数k。
结果输出:最小数。
输入实例:
178543
4
输出结果:
13
算法思想:所谓贪心算法,就是鼠目寸光地从局部看全局,首先得到局部的最优解,从而推导出全局的最优解。这道题中可以我们发现,若各位数字递增,则删除最后一个数字;否则删除第一个递减区间的首字符,这样删一位便形成了一个新的数字串。然后回到串首,按上述规则再删除下一个数字。这就是这道题的贪心选择性质,验证并且成立。并且具有最优子结构,对于正整数a,去掉其中k位,子问题就是正整数a删除一个数字时是新的数字最小的方案,求的的方案执行k次即可。
代码如下
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main(){
string s;
int k;
cin >> s >> k;
int tt=s.length()-k;
string ::iterator it;
for(int i=0;i<k;i++){
for(int j=1;j<s.length();j++){
if(s[j]<s[j-1]){
int t=j-1;
it=s.begin()+t;
s.erase(it);
break;
}
}
}
int x=0;
for(int i=0;i<s.length()&&i<tt;i++){
if(s[i]!='0'||x==1){
x=1;
cout <<s[i];
}
if(x==0&&s[i]=='0'){
continue;
}
}
}