题目

题目链接：剑指 Offer 59 - I. 滑动窗口的最大值
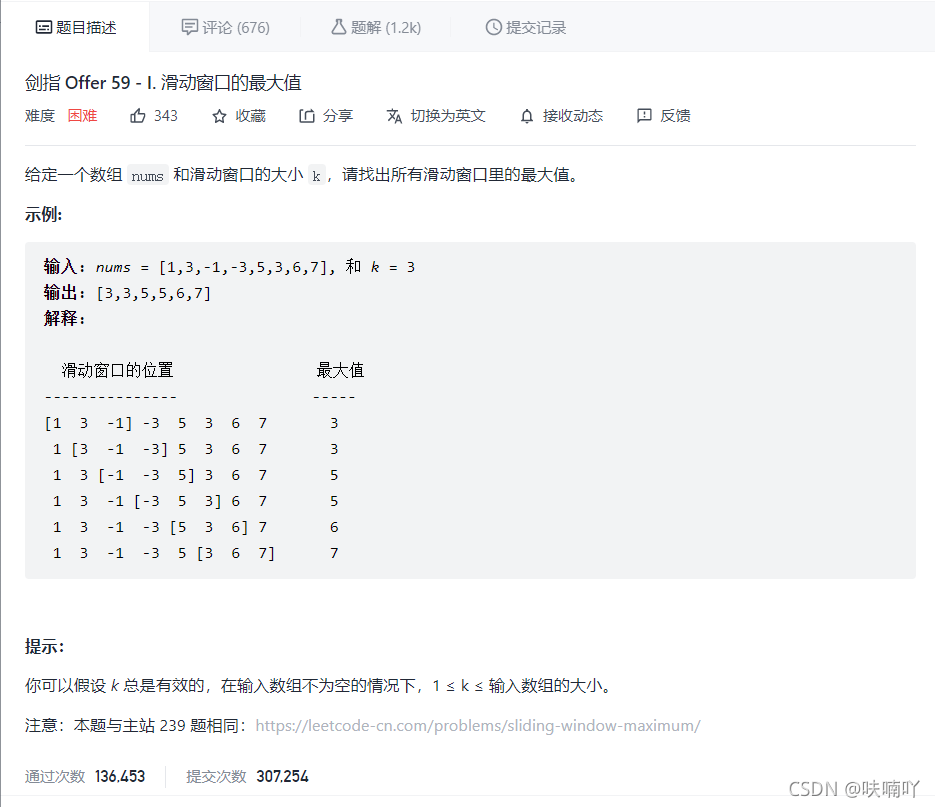
在这里插入图片描述

思路–单调队列

这道题暴力解法时间复杂度度是 O(n*k);
暴力的思路：

定义两个指针，一个是窗口的最后一个值的指针 i,另一个是窗口的第一个值得指针 w;
用 i 来遍历数组，同时判断窗口范围得最大值；
然后 i++，继续判断窗口得最大值；
直到 i 遍历完数组即可找出所有窗口得最大值，但是这样时间复杂度度是O(n * k);

单调队列思路：

搞两个指针w,i: w表示滑动窗口的弟一个指针;i一直遍历到最后i表示滑动窗口的值的最后一个指针;
再搞一个双端队列:双端队列的要求是双端队列的元素是逐渐减小的，也就是说这是一个递减的队列，单调递减队列；
首先队列为空，直接先入队:第一个i指向的值其次:滑动w,i，判断i的值是否小于队尾元素，小于即入队，大于即出队列元素，再入i指向的值:这样做的原因是为了保持单调队列都是递减的:
判断对头是否再滑动窗口的合理范围:在的话直接获取对头为滑动窗口的最大值;
假如队列的头的值，不在滑动窗口的合理范围那么就直接出对头再更新队头元素，此时对头就是滑动窗口最大值；
w没到合法值时候，都不需要更新最大值也不用检验队头是否在合法的窗，存放的是索引口范围；
队列为什么要放的不是值而是索引呢?因为我们需要判断对头的合法性，用对头的索引和w比较，假如是值，就无法判断合法性

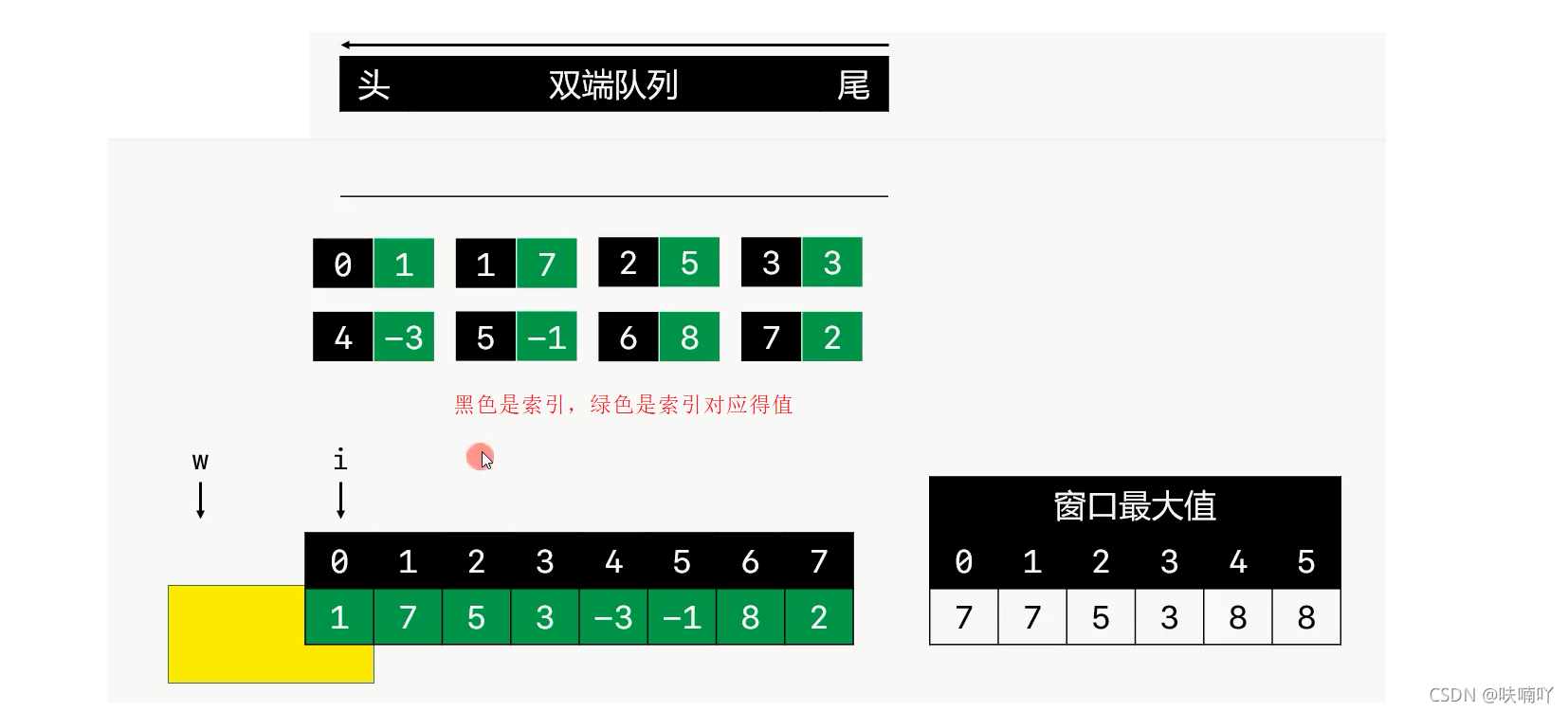
在这里插入图片描述

代码：

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
               
        deque<int> que; //存放索引，同时限制为单调递减队列，
                        //同时在滑动窗口的第一个值合法范围内时候，队头的索引就是窗口最大值的索引
    
        vector<int> maxVector ; //用来存滑动窗口最大值的数组
        //i是滑动窗口的最后一个值，同时i用来遍历数组nums
        for(int i = 0;i<nums.size();i++)
        {
            //如果发现滑动窗口的最后一个值比队尾还要大的话，那么就出队尾
            while(!que.empty() && nums[i] >= nums[que.back()])
            {
                que.pop_back();
            }
            //来到这里，说明滑动窗口的最后一个值比队尾小，那么就课入队nums[i]
            que.push_back(i);
            //入完nums[i],后要检验队头是否在合法的窗口中

            //如何检验是否队头在合法的窗口范围：
            //只要队头的值，也就是索引值，小于滑动窗口的第一个所以值那么就是说明不再合法范围了
            int w = i -k+1; //w为滑动窗口的第一个值
            //首先要判断w的合法性：因为刚开始w是不合法的，
            //不合法也就是不需要判断队头的值是否在滑动窗口的范围,也不需要把队头认为是最大值
            if(w <0) continue; //只要滑动窗口的第一个索引小于0就表示w不在合法范围

            //来到这里说明w合法了，那么就需要判断队头的索引是否合法，同时队头就是最大值

            if(que.front() < w) //队头不在窗口的合法范围
                que.pop_front(); 
            //来到这里说明队头是窗口合法范围
            //那么队头就是最大值了
            maxVector.push_back(nums[que.front()]);
        }
        return maxVector;
    }
};