【算法训练】 ^ 异或运算扩展

文章目录

【算法训练】 ^ 异或运算扩展

🎈🎆🎇 前言：

从这篇帖子开始也会逐渐的更新算法的帖子（有时间就来更新嘻嘻😁😁😁），很多人认为学习算法，就是以后会去当算法工程师，或者很NB的大佬搞算法搞研究，而我们以后不搞这些所以就不用学习算法，一看到算法就头痛什么的，以后不走这条路就可以不用看算法了，我也头痛，虽然你以后不去走算法工程师这个职业，但是面试的时候面试官会问到算法题的呀！！！，有90%的面试官会问到算法题和数据结构，只有仅仅10%运气好的人不会被问到，我们一般都是做最坏的打算，有备无患嘛，毕竟公司想选脑子好使的人才，算法题就是拉开差距的一种方式。算法不仅在面试的时候会被问到，当你进入工作写代码的时候也会遇到的，你的代码虽然会跑的出来，但是效率慢也是废的代码，所以代码需要优化，使运行效率更高就需要用到算法了，可想算法的地位也是很高的，还是认真学习吧。

不管什么语言在刚开始学习的时候都是会学运算符，这篇帖子来深入讲一讲^异或运算符及其扩展。

一、性质

1）、

0^a=a;
a^a=0;

相同位0，相异位1

也可以理解为无进制位相加；

2）、异或满足交换律和结合律

a^ b=b^ a, a^ b^ c=a^ (b^c)

有了这些性质，其实就可以做题了，😁😁😁😁

二、用 ^ 异或交换两个数

首先看到两个数的交换是不是很容易想到申请一个变量tmp，这次我们就不用申请一个额外的空间了让两个数直接交换。

public static void main(String[] args) {
        int a=11;//假设是‘甲’
        int b=22;//假设是‘乙’

        a=a^b;//a=甲^乙      b=乙
        b=a^b;//a=甲^乙      b=甲^乙^乙=甲
        a=a^b;//a=甲^乙  ^甲 =乙       b=甲
    
        System.out.println(a);
        System.out.println(b);
}

用 ^可以节省额外的一个空间，这就是算法的优化，现在有人会想是不是以后交换都可以这么用了，可万万不能，运用这种算法是有条件的，条件就是a和b必须是在两个空间，同一个数也行，但是他们必须是两个空间，我们就会想到快排中的Hoare方法中swap，这个就不能这么用了，因为最后两个会相遇到一个空间上面去，都^ 成0了，所以用之前记住条件是在不同空间上。

三、面试题

1）、一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这一个数

2）、一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到这两个数

思路：

第一题的思路很简单是给第二题做铺垫的，第一题运用性质异或遍历数组，最后单独的就是奇数
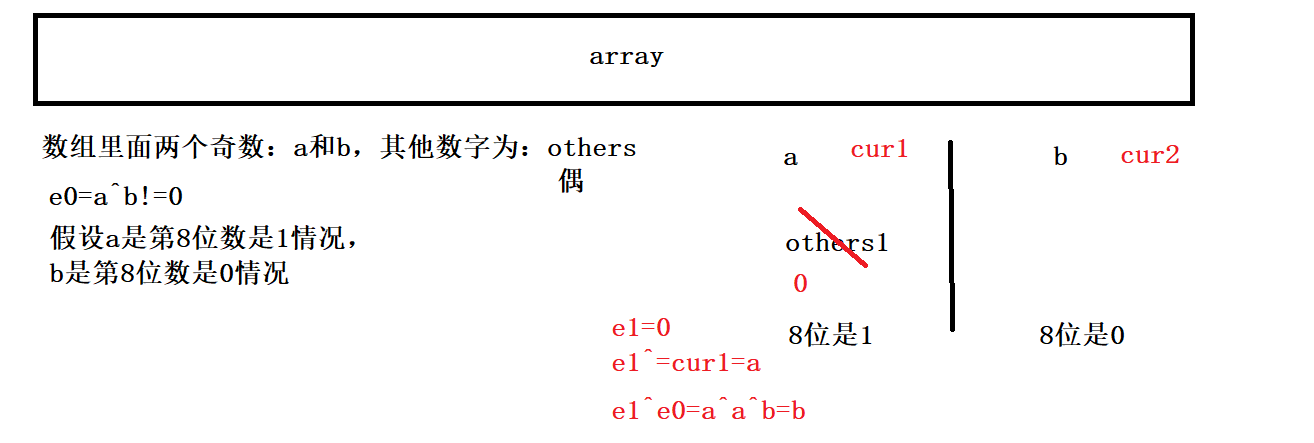
第二题稍微复杂点，数组中有两个奇数，那么这两个数肯定不相等 ,两数^ ！=0，所以这两数中的某一位数要么是1要么是0，所以就分为了数组中某数位是1的情况，某数位是0的情况，假设这两个奇数是a和b，a在某数位是1的情况里，b在某数位是0的情况里，定义一个变量e1，某数位是1的那一组数都^成0最后剩下a，那么这个e1 变量^ab=a^ab=b,

代码：

public class TestDemo {
    public static void printOddTinesNum1(int[] array) {
        int e0=0;
        for (int cur:array) {
            e0=e0^cur;

        }
        System.out.println(e0);
    }


    public static void printOddTimesNum2(int[] array) {
        int e0=0;
        for (int cur:array) {
            e0=e0^cur;
        }
        /**
         * e0=a^b;
         * e0!=0
         * e0必然有个位置=1
         */
        int rightOne=e0 & (~e0+1);//提取出最右侧的1

        int e1=0;
        for (int cur:array) {
            if((cur & rightOne)==1) {//两边分类了，某位为1的  or  0的
                e1=e1^cur;
                //留下了a or b;
            }
        }
        System.out.println(e1+ " " + (e1^e0));

    }
    public static void main(String[] args) {  
        int[] arr1 = { 3, 3, 2, 3, 1, 1, 1, 3, 1, 1, 1 };
        printOddTinesNum1(arr1);

        int[] arr2 = { 4, 3, 4, 2, 2, 2, 4, 1, 1, 1, 3, 3, 1, 1, 1, 4, 2, 2 };
         printOddTimesNum2(arr2);
    }
}