[数据结构与算法] 图的广度优先遍历实现

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 图的广度优先遍历实现 -> 正文阅读

[数据结构与算法]图的广度优先遍历实现

文章目录

题目描述

图的广度优先遍历实现
要求：
1、以邻接表形式构造图；
2、打印输出邻接表；
3、输出：广度优先遍历序列；

输入：
顶点数、边数目。
点、边集合表示（1代表存在边，0代表不存在边）
输出：
（1）边逻辑正确，则输出：“输入正确！”
（2）边逻辑不正确，则输出：“输入边数不对！程序退出！！“
（3）输出邻接表存储；
（4）输出广义遍历结果。

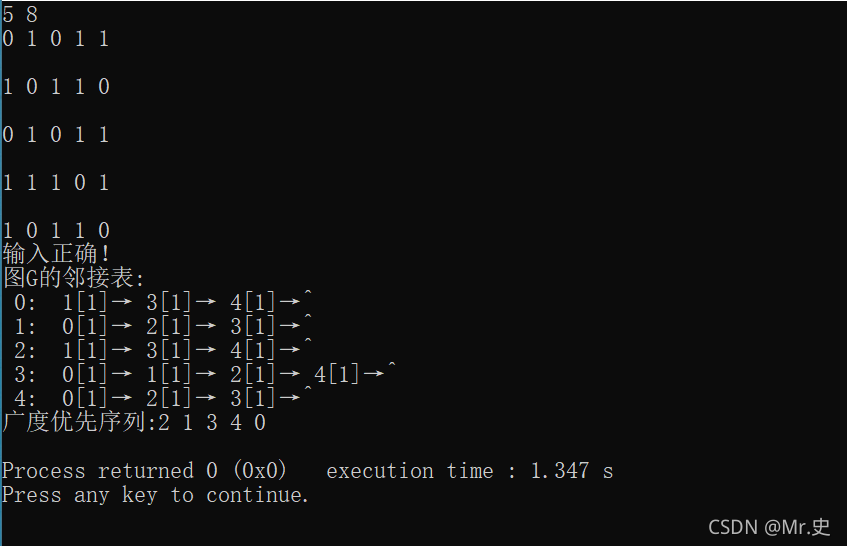
输入

5 8 // 5代表顶点数， 8 代表边数目
0 1 0 1 1

1 0 1 1 0

0 1 0 1 1

1 1 1 0 1

1 0 1 1 0

输出

输入正确！
图G的邻接表:
0: 1[1]→ 3[1]→ 4[1]→∧
1: 0[1]→ 2[1]→ 3[1]→∧
2: 1[1]→ 3[1]→ 4[1]→∧
3: 0[1]→ 1[1]→ 2[1]→ 4[1]→∧
4: 0[1]→ 2[1]→ 3[1]→∧
广度优先序列: 2 1 3 4 0

样例输入

5 8
0 1 0 1 1

1 0 1 1 0

0 1 0 1 1

1 1 1 0 1

1 0 1 1 1

样例输出

输入边数不对！程序退出！！

代码实现

(1)、图的创建输出销毁

#include <iostream>
#include <stdlib.h>

using namespace std;

#define MAXV 100
#define INF 32767   //定义无穷

typedef int InfoType;

//边
typedef struct ANode
{
    int adjvex;
    struct ANode *nextarc;
    int weight;
} ArcNode;

//顶点
typedef struct Vnode
{
    InfoType info;
    ArcNode *firstarc;
} VNode;

//图
typedef struct
{
    VNode adjlist[MAXV];
    int n, e;
}AdjGraph;


//创建图运算算法
void GreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
    int i, j;
    ArcNode *p;
    G = (AdjGraph *)malloc(sizeof(AdjGraph));
    //给邻接表中所有头结点的指针域置初值
    for(i = 0; i < n; i++)
    {
        G->adjlist[i].firstarc = NULL;
    }
    //检查邻接矩阵中的每个元素
    for(i = 0; i < n; i++)
    {
        for(j = n-1; j >= 0; j--)
        {
            //存在一条边
            if(A[i][j] != 0 && A[i][j] != INF)
            {
                //创建一个结点p
                p = (ArcNode *)malloc(sizeof(ArcNode));
                //存放邻接结点
                p->adjvex = j;
                //存放权
                p->weight = A[i][j];
                //采用头插法插入结点p
                p->nextarc = G->adjlist[i].firstarc;
                G->adjlist[i].firstarc = p;
            }
        }
    }
    G->n = n;
    G->e = e;
}


//输出图的运算算法
void DispAdj(AdjGraph *G)
{
    int i;
    ArcNode *p;

    for(i = 0; i < G->n; i++)
    {
        p = G->adjlist[i].firstarc;
        cout<<i<<":   ";
        while(p != NULL)
        {
            cout<<p->adjvex<<"["<<p->weight<<"]"<<"-> ";
            p = p->nextarc;
        }
        cout<<"^"<<endl;
    }
}

//销毁图的运算算法
void DistroyAdj(AdjGraph *&G)
{
    int i;
    ArcNode *pre, *p;
    //扫描所有单链表
    for(i = 0; i < G->n; i++)
    {
        //p指向第i个单链表的头结点
        pre = G->adjlist[i].firstarc;
        if(pre != NULL)
        {
            p = pre->nextarc;
            //释放第i个单链表的所有边结点
            while(p != NULL)
            {
                free(pre);
                pre = p;
                p = p->nextarc;
            }
            free(pre);
        }
    }
    //释放头结点数组
    free(G);
}



int main()
{
    AdjGraph *G;
    int A[MAXV][MAXV];
    int n;
    int e;
    int sum = 0;

    //输入顶点数
    cin>>n;
    //输入边的个数
    cin>>e;

    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            cin>>A[i][j];
            if(A[i][j] == 1)
            {
                sum++;
            }
        }
    }
    
    if(sum != 2*e)
    {
        cout<<"输入边数不对！程序退出！！"<<endl;
        return 0;
    }
    cout<<"输入正确！"<<endl;
    cout<<"图G的邻接表:"<<endl;
    //创建图
    GreateAdj(G, A, n, e);

    //打印图
    DispAdj(G);

    //销毁图
    DistroyAdj(G);

    return 0;
}

(2)、含广度优先遍历实现代码（c++）

#include <iostream>
#include <stdlib.h>

using namespace std;

#define MAXV 100
#define MaxSize 10
#define INF 32767   //定义无穷

typedef int InfoType;
typedef int ElemType;


//边
typedef struct ANode
{
    int adjvex;
    struct ANode *nextarc;
    int weight;
} ArcNode;

//顶点
typedef struct Vnode
{
    InfoType info;
    ArcNode *firstarc;
} VNode;

//图
typedef struct
{
    VNode adjlist[MAXV];
    int n, e;
}AdjGraph;

typedef struct
{
    ElemType data[MaxSize];
    int front, rear;
} SqQueue;


//创建图运算算法
void GreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
    int i, j;
    ArcNode *p;
    G = (AdjGraph *)malloc(sizeof(AdjGraph));
    //给邻接表中所有头结点的指针域置初值
    for(i = 0; i < n; i++)
    {
        G->adjlist[i].firstarc = NULL;
    }
    //检查邻接矩阵中的每个元素
    for(i = 0; i < n; i++)
    {
        for(j = n-1; j >= 0; j--)
        {
            //存在一条边
            if(A[i][j] != 0 && A[i][j] != INF)
            {
                //创建一个结点p
                p = (ArcNode *)malloc(sizeof(ArcNode));
                //存放邻接结点
                p->adjvex = j;
                //存放权
                p->weight = A[i][j];
                //采用头插法插入结点p
                p->nextarc = G->adjlist[i].firstarc;
                G->adjlist[i].firstarc = p;
            }
        }
    }
    G->n = n;
    G->e = e;
}


//输出图的运算算法
void DispAdj(AdjGraph *G)
{
    int i;
    ArcNode *p;

    for(i = 0; i < G->n; i++)
    {
        p = G->adjlist[i].firstarc;
        cout<<" "<<i<<": ";
        while(p != NULL)
        {
            cout<<" "<<p->adjvex<<"["<<p->weight<<"]"<<"→";
            p = p->nextarc;
        }
        cout<<"^"<<endl;
    }
}

//销毁图的运算算法
void DistroyAdj(AdjGraph *&G)
{
    int i;
    ArcNode *pre, *p;
    //扫描所有单链表
    for(i = 0; i < G->n; i++)
    {
        //p指向第i个单链表的头结点
        pre = G->adjlist[i].firstarc;
        if(pre != NULL)
        {
            p = pre->nextarc;
            //释放第i个单链表的所有边结点
            while(p != NULL)
            {
                free(pre);
                pre = p;
                p = p->nextarc;
            }
            free(pre);
        }
    }
    //释放头结点数组
    free(G);
}

void InitQueue(SqQueue *&q)
{
    q = (SqQueue *)malloc(sizeof(SqQueue));
    q->front = q->rear = 0;
}


void DestroyQueue(SqQueue *&q)
{
    free(q);
}

bool QueueEmpty(SqQueue *q)
{
    return (q->front == q->rear);
}

bool enQueue(SqQueue *&q, ElemType e)
{
    if((q->rear+1)%MaxSize == q->front)
    {
        //printf("队列已满，%d进队不成功！\n", e);
        cout<<"队列已满，%d进队不成功！\n"<<e;
        return false;
    }

    q->rear = (q->rear+1)%MaxSize;
    q->data[q->rear] = e;
    return true;

}

bool deQueue(SqQueue *&q, ElemType &e)
{
    if(q->front == q->rear)
        return false;
    q->front = (q->front + 1)%MaxSize;
    e = q->data[q->front];
    return true;
}

//广度优先序列
void BFS(AdjGraph *G, int v)
{
    int w, i;
    ArcNode *p;
    SqQueue *qu;
    InitQueue(qu);
    int visited[MAXV];
    for(i = 0; i < G->n; i++)
    {
        visited[i] = 0;
    }
    cout<<"广度优先序列:"<<v;
    visited[v] = 1;
    enQueue(qu, v);
    while(!QueueEmpty(qu))
    {
        deQueue(qu, w);
        p = G->adjlist[w].firstarc;
        while(p != NULL)
        {
            if(visited[p->adjvex] == 0)
            {
                cout<<" "<<p->adjvex;
                visited[p->adjvex] = 1;
                enQueue(qu, p->adjvex);
            }
            p = p->nextarc;
        }

    }
    cout<<endl;
}

int main()
{
    AdjGraph *G;
    int A[MAXV][MAXV];
    int n;
    int e;
    int sum = 0;

    //输入顶点数
    cin>>n;
    //输入边的个数
    cin>>e;

    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            cin>>A[i][j];
            if(A[i][j] == 1)
            {
                sum++;
            }
        }
    }

    if(sum != 2*e)
    {
        cout<<"输入边数不对！程序退出！！"<<endl;
        return 0;
    }
    cout<<"输入正确！"<<endl;
    cout<<"图G的邻接表:"<<endl;
    //创建图
    GreateAdj(G, A, n, e);

    //打印图
    DispAdj(G);
    
    int v = 2;
    BFS(G, v);
    //销毁图
    DistroyAdj(G);

    return 0;
}

(3)、含广度优先遍历实现代码（C）

//广度优先遍历算法

#define MaxSize 100

//图的基本运算算法
#include <stdio.h>
#include <malloc.h>
//图的两种存储结构
#define INF 32767				//定义∞
#define	MAXV 100				//最大顶点个数
typedef char InfoType;
#include<iostream>
using namespace std;
//以下定义邻接矩阵类型
typedef struct
{	int no;						//顶点编号
	InfoType info;				//顶点其他信息
} VertexType;					//顶点类型
typedef struct
{	int edges[MAXV][MAXV];		//邻接矩阵数组
	int n,e;					//顶点数，边数
	VertexType vexs[MAXV];		//存放顶点信息
} MatGraph;						//完整的图邻接矩阵类型

//以下定义邻接表类型
typedef struct ANode
{	int adjvex;					//该边的邻接点编号
	struct ANode *nextarc;		//指向下一条边的指针
	int weight;					//该边的相关信息，如权值（用整型表示）
} ArcNode;						//边结点类型
typedef struct Vnode
{	InfoType info;				//顶点其他信息
	int count;					//存放顶点入度,仅仅用于拓扑排序
	ArcNode *firstarc;			//指向第一条边
} VNode;						//邻接表头结点类型
typedef struct 
{	VNode adjlist[MAXV];		//邻接表头结点数组
	int n,e;					//图中顶点数n和边数e
} AdjGraph;						//完整的图邻接表类型

void CreateMat(MatGraph &g,int A[MAXV][MAXV],int n,int e) //创建图的邻接矩阵
{
	int i,j;
	g.n=n; g.e=e;
	for (i=0;i<g.n;i++)
		for (j=0;j<g.n;j++)
			g.edges[i][j]=A[i][j];
}
void DispMat(MatGraph g)	//输出邻接矩阵g
{
	int i,j;
	for (i=0;i<g.n;i++)
	{
		for (j=0;j<g.n;j++)
			if (g.edges[i][j]!=INF)
				printf("%4d",g.edges[i][j]);
			else
				printf("%4s","∞");
		printf("\n");
	}
}

void CreateAdj(AdjGraph *&G,int A[MAXV][MAXV],int n,int e) //创建图的邻接表
{
	int i,j;
	ArcNode *p;
	G=(AdjGraph *)malloc(sizeof(AdjGraph));
	for (i=0;i<n;i++)								//给邻接表中所有头结点的指针域置初值
		G->adjlist[i].firstarc=NULL;
	for (i=0;i<n;i++)								//检查邻接矩阵中每个元素
		for (j=n-1;j>=0;j--)
			if (A[i][j]!=0 && A[i][j]!=INF)			//存在一条边
			{	p=(ArcNode *)malloc(sizeof(ArcNode));	//创建一个结点p
				p->adjvex=j;
				p->weight=A[i][j];
				p->nextarc=G->adjlist[i].firstarc;	//采用头插法插入结点p
				G->adjlist[i].firstarc=p;
			}
	G->n=n; G->e=n;
}
void DispAdj(AdjGraph *G)	//输出邻接表G
{
	int i;
	ArcNode *p;
	for (i=0;i<G->n;i++)
	{
		p=G->adjlist[i].firstarc;
		printf("%3d: ",i);//"  0:   "
		while (p!=NULL)
		{
			printf("%3d[%d]→",p->adjvex,p->weight);
			p=p->nextarc;
		}
		printf("∧\n");
	}
}
void DestroyAdj(AdjGraph *&G)		//销毁图的邻接表
{	int i;
	ArcNode *pre,*p;
	for (i=0;i<G->n;i++)			//扫描所有的单链表
	{	pre=G->adjlist[i].firstarc;	//p指向第i个单链表的首结点
		if (pre!=NULL)
		{	p=pre->nextarc;
			while (p!=NULL)			//释放第i个单链表的所有边结点
			{	free(pre);
				pre=p; p=p->nextarc;
			}
			free(pre);
		}
	}
	free(G);						//释放头结点数组
}

typedef int ElemType;
typedef struct 
{	
	ElemType data[MaxSize];
	int front,rear;		//队首和队尾指针
} SqQueue;
void InitQueue(SqQueue *&q)
{	q=(SqQueue *)malloc (sizeof(SqQueue));
	q->front=q->rear=0;
}
void DestroyQueue(SqQueue *&q)
{
	free(q);
}
bool QueueEmpty(SqQueue *q)
{
	return(q->front==q->rear);
}
bool enQueue(SqQueue *&q,ElemType e)
{	if ((q->rear+1)%MaxSize==q->front)	//队满上溢出
		return false;
	q->rear=(q->rear+1)%MaxSize;
	q->data[q->rear]=e;
	return true;
}
bool deQueue(SqQueue *&q,ElemType &e)
{	if (q->front==q->rear)				//队空下溢出
		return false;
	q->front=(q->front+1)%MaxSize;
	e=q->data[q->front];
	return true;
}


void BFS(AdjGraph *G,int v)  
{
	int w,i;
	ArcNode *p;
	SqQueue *qu;							//定义环形队列指针
	InitQueue(qu);							//初始化队列
	int visited[MAXV];            			//定义顶点访问标志数组
	for (i=0;i<G->n;i++) visited[i]=0;		//访问标志数组初始化
	printf("%2d",v); 						//输出被访问顶点的编号
	visited[v]=1;              				//置已访问标记
	enQueue(qu,v);
	while (!QueueEmpty(qu))       			//队不空循环
	{	
		deQueue(qu,w);						//出队一个顶点w
		p=G->adjlist[w].firstarc; 			//指向w的第一个邻接点
		while (p!=NULL)						//查找w的所有邻接点
		{	
			if (visited[p->adjvex]==0) 		//若当前邻接点未被访问
			{
				printf("%2d",p->adjvex);  	//访问该邻接点
				visited[p->adjvex]=1;		//置已访问标记
				enQueue(qu,p->adjvex);		//该顶点进队
           	}
           	p=p->nextarc;              		//找下一个邻接点
		}
	}
	printf("\n");
}

int main()
{	int sum1=0;
	int sum0=0;
	AdjGraph *G;
	int A[MAXV][MAXV]={{0,1,0,1,1},{1,0,1,1,0},
			{0,1,0,1,1},{1,1,1,0,1},{1,0,1,1,0}};
	int n=5, e=8;
	cin>>n>>e;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cin>>A[i][j];
		}
	}
	for(int i1=0;i1<n;i1++){
		for(int j1=0;j1<n;j1++){
			if(A[i1][j1]==1){sum1=sum1+1;}
			if(A[i1][j1]==0){sum0=sum0+1;}
		}
	}
	if(sum1==2*e&&sum0==n*n-2*e){
		cout<<"输入正确！"<<endl;
	}else{
		cout<<"输入边数不对！程序退出！！"<<endl;
		return 0;
	}
	CreateAdj(G,A,n,e);			//建立《教程》中图8.1(a)的邻接表

	printf("图G的邻接表:\n");
	DispAdj(G);					//输出邻接表G
	printf("广度优先序列:");BFS(G,2);printf("\n");
	DestroyAdj(G);				//销毁邻接表
	return 1;
}