A. balloon
题目大意:
潇湘有小孩和mm的气球。
今天下课后,我的朋友们要去抓这些气球。每个气球在墙上都有一定的高度。只有当孩子跳起来时,他们的手所能达到的高度大于或等于气球的高度,孩子才能拿起气球。
为了公平起见,老师让跳得低的孩子先摘,跳得高的孩子再摘。
孩子们是非常贪心的,每个孩子在摘气球的时候都会摘下所有他能摘到的气球。
巧合的是,孩子们在跳起来的时候可以达到不同的高度,这样同样高度的孩子在跳起来之后就不会有纠纷了。

简单的模拟,直接上代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e5+10;
typedef pair<int,int> PII;
int b[N];
PII a[N];
int n,m;
int res[N];
int main(){
memset(res,0,sizeof res);
scanf ("%d%d",&n,&m);
for (int i=1;i<=n;i++)
{
int x;
scanf ("%d",&x);
a[i] = {x,i};
}
for (int i=1;i<=m;i++) scanf ("%d",&b[i]);
sort(a+1,a+1+n);
sort(b+1,b+1+m);
int j=1;
for (int i=1;i<=n;i++)
{
int h = a[i].first,cnt=0;
while (h>=b[j]&&j<=m)
{
cnt++;
j++;
}
res[a[i].second] = cnt;
}
for (int i=1;i<=n;i++)
printf ("%d\n",res[i]);
return 0;
}
B. sophistry
题目大意:
在小K的QQ群里,小T总是变得越来越奇怪。
小T将在小组发言n天,小K的愤怒值m。
小T每天都有一个能力值,第i天的能力值是ai
每一天,小T都会选择是否嘲笑小K。如果小T选择在第2天嘲笑小K,小K就会被a2伤害
我在此基础上,如果小T的能力值ai我?
超过了小K的愤怒值m,小K将勃然大怒,并禁止小T在d天内使用。也就是说,在i+1, i+2,…min (i + n) i + 1, + 2,…,min (i + d, n)天,肖T将被禁止。
现在,肖T想把对肖K的伤害最大化,但是肖T太坏了解决不了这个问题,所以他找到了你。希望你能帮他解决这个问题。你只需要找出Xiao T对Xiao K造成的最大损害。
题目一看就是决策问题,动态规划,每天小T都会决策是否嘲笑小K,而限制条件是当ai>m时,小K会产生不产生价值的缓冲期,这样后面会有一些状态不能再决策,当时做的时候,另一个队员发现每天都是相互独立的,如果倒叙转移的话,就可以简化了。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
long long dp[N],a[N];
int main()
{
int n,d,m;
cin >> n >> d >> m;
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=n;i>=1;i--)
{
if(a[i]<=m)dp[i]=dp[i+1]+a[i];
else
dp[i]=max(dp[i+1+d]+a[i],dp[i+1]);
}
cout <<dp[1];
}
D. maxsum
题目大意:
给你一个数组,让你求前w大的子数组和。
一个简单的贪心,很容易想到所有方案都被枚举
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<map>
using namespace std;
typedef long long LL;
const int N = 1e5+10;
int a[N];
struct Node{
int l,r;
LL sum;
bool operator <(const Node &t)const
{
return sum<t.sum;
}
};
priority_queue<Node> p;
map<pair<int,int>,bool> mh;
int n,w;
int main(){
LL s=0;
scanf ("%d%d",&n,&w);
for (int i=1;i<=n;i++)
{
scanf ("%d",&a[i]);
s+=a[i];
}
p.push({1,n,s});
while (w--)
{
auto t = p.top();
p.pop();
printf ("%lld ",t.sum);
int l = t.l,r = t.r;
if (!mh[{l+1,r}])
p.push({l+1,r,t.sum-a[l]});
if (!mh[{l,r-1}])
p.push({l,r-1,t.sum-a[r]});
mh[{l,r-1}] = mh[{l+1,r}]= true;
}
return 0;
}
E. array
题目大意:
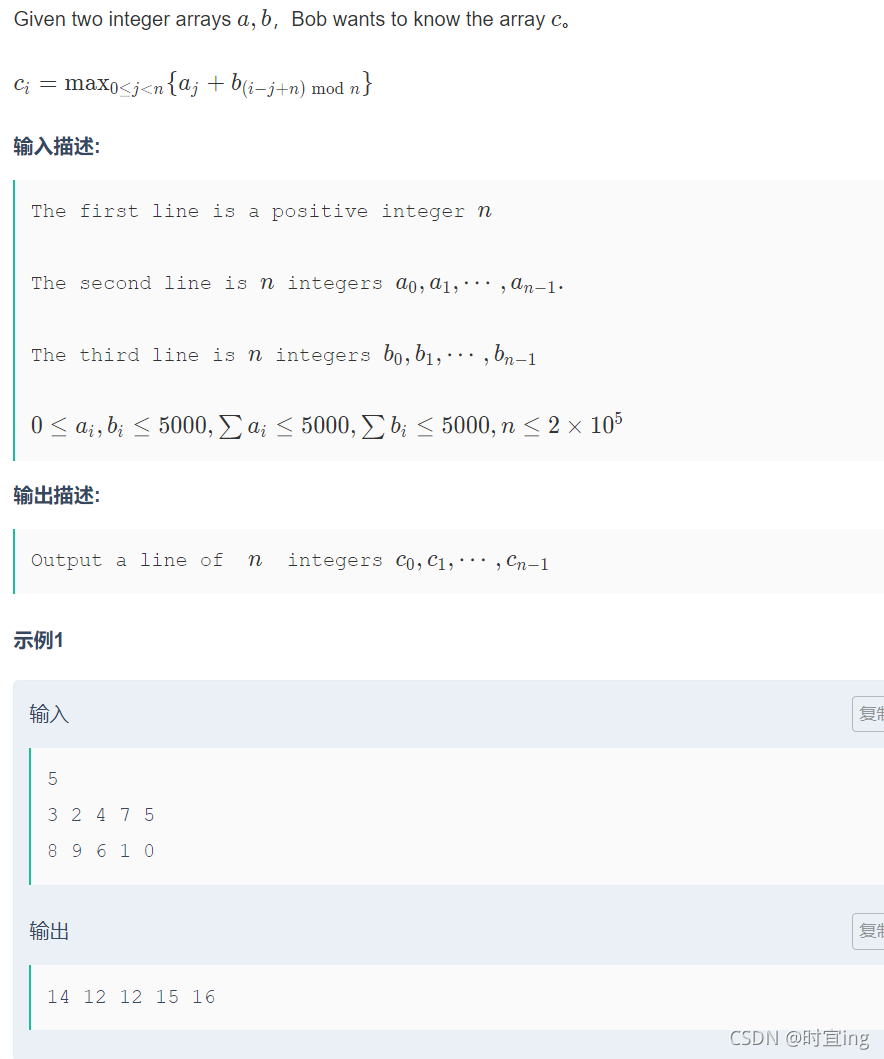
题意言简意赅,该题的重点是发现输入描述的范围,发现a,b数组里大多数都是零。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 2e5+10;
int a[N],b[N],res[N];
int c[N],d[N],cnt1=0,mx=-1,cnt2=0;
int main()
{
int n;
scanf ("%d",&n);
for (int i=0;i<n;i++)
{
scanf ("%d",&a[i]);
if (a[i]!=0)
c[cnt1++] = i;
mx = max(mx,a[i]);
}
for (int i=0;i<n;i++)
{
scanf ("%d",&b[i]);
if (b[i]!=0)
d[cnt2++] = i;
mx = max(mx,b[i]);
}
for (int i=0;i<cnt1;i++)
{
for (int j=0;j<cnt2;j++)
{
res[(c[i]+d[j])%n] = max(res[(c[i]+d[j])%n],a[c[i]]+b[d[j]]);
}
}
for (int i=0;i<n;i++)
{
if (i!=n-1)
printf ("%d ",max(res[i],mx));
else
printf("%d\n",max(res[i],mx));
}
return 0;
}
这次比赛发现很多题并不是不会,而是需要去不断尝试,发现。