[数据结构与算法]2021牛客寒假算法基础集训营2 E 双指针建图 BFS 思维

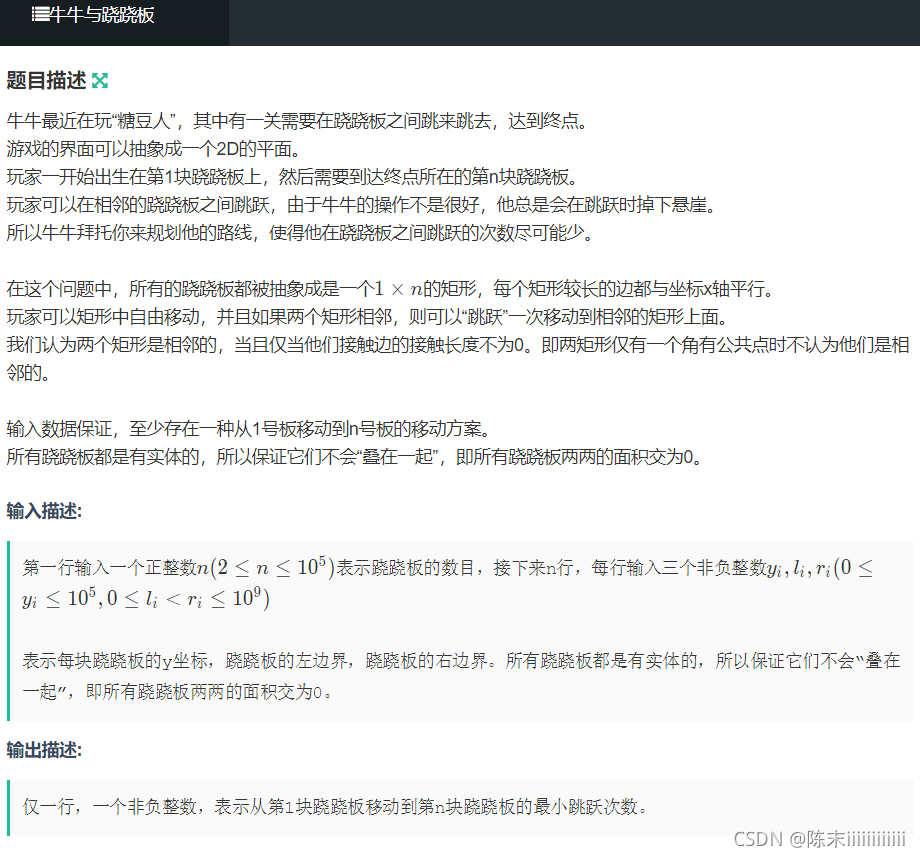
题目

题解思路

很容易看出这题就是裸的BFS，但是怎么建图呢？
这里用到了双指针。

用桶装每个高度，再将桶内的跷跷板从左到右排序。

从最低高度开始从左往右从下到上建边。

从左到右建图的话直接看是否满足题目条件即可。
从下到上就有讲究了。

你得先看看上面有没有点，其次要贪心的试探，上一层的这个位置点是否能建边，小了就往前跑，跑到可以建为止，并且建的时候也需要往前跑，跑到不能建的时候记得回溯（即从左到右的下一个点可能可以和前一个点的最后一个位置建边。）

这样每个点最多只会被跑2次，时间复杂度是On的。
建完了就直接BFS即可。

AC代码

#include <bits/stdc++.h>
//#include <unordered_map>
//priority_queue
#define PII pair<int,int>
#define ll long long

using namespace std;

const  int  INF =  0x3f3f3f3f;
const  int N = 100010 ; 
struct node
{
    int p , l , r ;
};
vector <node> h[N] ; 
bool cmp (node A ,node B )
{
    return A.l < B.l ;
}
vector <int> head[N] ; 
int vis[N] ; 
int n ; 
void bfs()
{
    queue <PII> q ;
    q.push({1,0});
    vis[1] = 1 ; 
    while (!q.empty())
    {
        auto tmp = q.front() ;
        q.pop();
        int sp = tmp.first ; 
        if (sp == n )
        {
            cout << tmp.second << "\n" ;
            return ;
        }
        for (int i = 0 ; i < head[sp].size() ; i++ )
        {
            int sk = head[sp][i] ;
            if (!vis[sk])
            {
                vis[sk] = 1 ;
                q.push({sk,tmp.second+1});
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    cin >> n ;
    int sh = INF ,eh = -1 ; 
    for (int i = 1 ; i <= n ; i++ )
    {
        int t1 , t2 , t3 ; 
        cin >> t1 >> t2 >> t3 ; 
        h[t1].push_back({i,t2,t3});
        sh = min(t1,sh) ; 
        eh = max(t1,eh) ;
    }
    //cout << sh << " " << eh << "\n";
    for (int i = sh ; i <= eh ; i++ )
        sort(h[i].begin(),h[i].end(),cmp);
    /*
    for (int i = sh ; i <= eh ; i++ )
    {
        for (int j = 0 ; j < h[i].size() ; j++ )
            cout << h[i][j].p << " " ;
        cout << "\n" ; 
    }
    cout << "\n" ; */
    for (int i = sh ; i <= eh ; i++ )
    {
        int pit = -1 ;
        for (int j = 0 ;  j < h[i].size() ; j++ )
        {
            int t1 = h[i][j].l , t2 = h[i][j].r ;
            if ( j + 1 < h[i].size() )
            {
                int t3 = h[i][j+1].l ;
                if ( t3 <= t2 )
                {
                    int p1 = h[i][j].p;
                    int p2 = h[i][j+1].p;
                    head[p1].push_back(p2) ;
                    head[p2].push_back(p1) ;
                }
            }
            if ( i != eh )
            {
                if (pit == -1 )
                {
                    int sz = h[i+1].size() ; 
                    if ( sz != 0)
                    {
                        int k = 0 ; 
                        while ( k < sz && h[i+1][k].r <= t1 )
                            k++ ;
                        while ( k < sz && h[i+1][k].r > t1 && h[i+1][k].l < t2 )
                        {
                            int sp = h[i][j].p ; 
                            int sp2 = h[i+1][k].p ; 
                            head[sp].push_back(sp2) ;
                            head[sp2].push_back(sp) ; 
                            k++;
                        }
                        k--;
                        pit = k ; 
                    }
                }else
                {
                    int sz = h[i+1].size() ; 
                    int k = pit ; 
                    while ( k < sz && h[i+1][k].r <= t1 )
                        k++ ;
                    while ( k < sz && h[i+1][k].r > t1 && h[i+1][k].l < t2 )
                    {
                        int sp = h[i][j].p ; 
                        int sp2 = h[i+1][k].p ; 
                        head[sp].push_back(sp2) ;
                        head[sp2].push_back(sp) ; 
                        k++;
                    }
                    if (pit != k )
                    {
                        k--;
                        pit = k ; 
                    }else
                    {
                        k = sz + 1 ;
                    }
                }
            }
        }
    }
    /*
    for (int i = 1 ; i <= n ; i++ )
    {
        for (int j = 0 ; j <head[i].size() ; j++ )
        {
            cout << i << " " << head[i][j] << "\n" ; 
        }
    }*/
    bfs();
    return 0 ;
}