[数据结构与算法]iOS LeetCode ? 完美矩形

给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

示例 1：

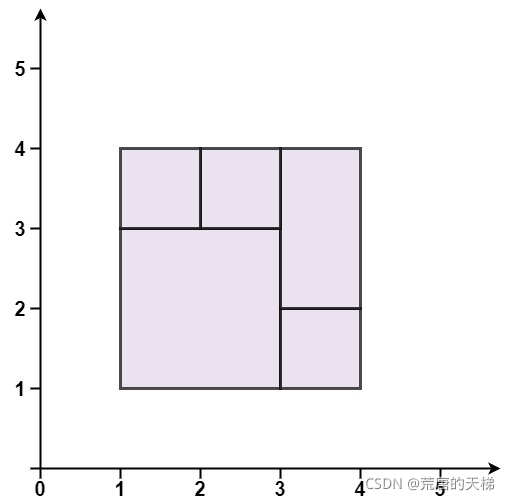
输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。 

示例 2：

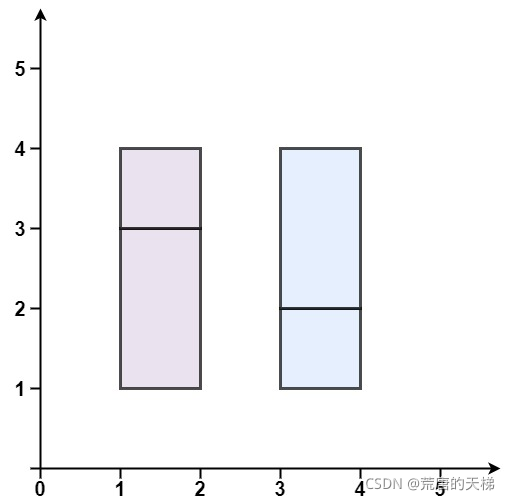
输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

示例 3：

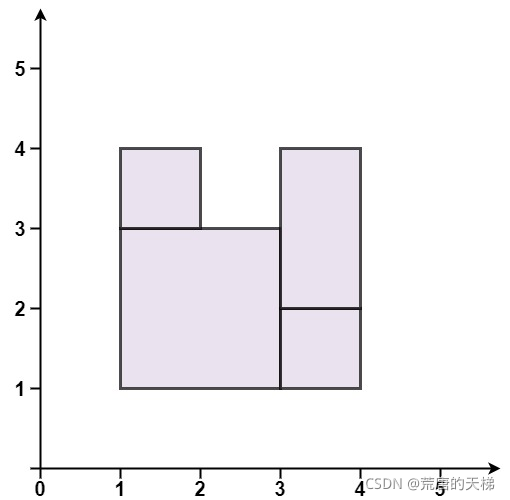
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出：false
解释：图形顶端留有空缺，无法覆盖成一个矩形。

示例 4：

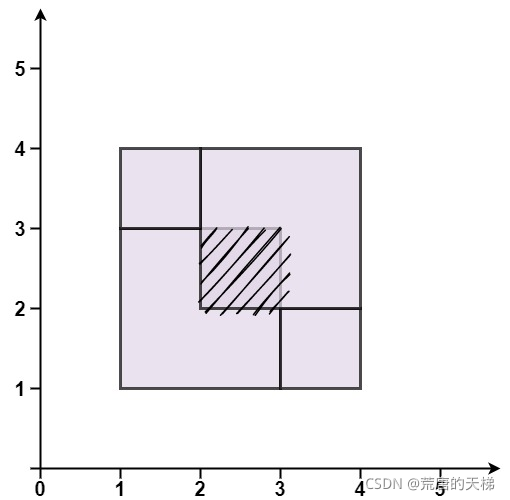
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

提示：

• 1 <= rectangles.length <= 2 * 10⁴
• rectangles[i].length == 4
• -10⁵ <= xi, yi, ai, bi <= 10⁵

解题思路

这道题可以使用扫描线来做，扫描线理解起来比较简单，但是，代码着实难写，所以，我们使用一种更容易理解的方法：找规律！

题目要求：所有矩形一起 精确 覆盖了某个矩形区域，可以得出以下几个结论：

• 不能出现空缺；
• 不能出现重叠；
• 所有小矩形合在一起是大矩形；

通过以上结论，我们可知，所有小矩形的面积之和等于大矩形的面积，所以，我们可以先找出大矩形的左下角和右上角，然后求出所有小矩形的面积之和与大矩形的面积比较，如果不相等，可以直接返回 false。

那么，是否只考虑面积相等就可以了呢？

显然不行，因为有可能正好空缺一块，且重叠一块，这样算出来的总面积也会相等，但不能做到精确覆盖，所以，我们还需要考虑其他条件。

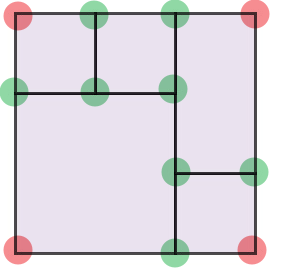
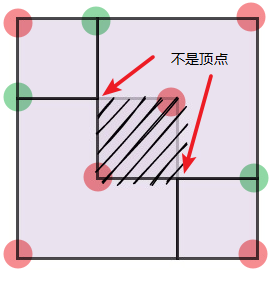
观察下面两图，左边为完美矩形，右边为非完美矩形，在完美矩形中，除了四个顶点之外，其它相交的点出现的次数都是偶数次，而非完美矩形不符合这个条件，所以，我们可以检测出现一次的点的数量，并检测它们是不是正好为四个顶点。

代码

	// 391. 完美矩形
    func isRectangleCover(_ rectangles: [[Int]]) -> Bool {
        
        // 计算每个小矩形面积是否等于大矩形面积
        // 看每个顶点出现的次数，如果最后出现一次的顶点不是四个，则说明不符合完美矩形
        var area = 0
        var set = Set<Int>()
        
        func key(_ x: Int, _ y: Int) -> Int {
            // 二维坐标转一维，方便比较
            // 10000007 是随便取的一个大质数
            // 这里既是溢出了也没什么问题
            return x * 100000007 + y
        }
        
        func record(_ x: Int, _ y: Int) {
            // 记录顶点出现的次数，如果一个顶点出现偶数次，则移除
            let key = key(x, y)
            if set.contains(key) {
                set.remove(key)
            } else {
                set.insert(key)
            }
        }
        
        // 记录大矩形的左下角和右上角
        var a1 = Int.max, b1 = Int.max
        var a2 = Int.min, b2 = Int.min
        
        for rectangle in rectangles {
            // 小矩形的坐标
            let x1 = rectangle[0], y1 = rectangle[1]
            let x2 = rectangle[2], y2 = rectangle[3]
            
            // 计算左下角
            if x1 < a1 || y1 < b1 {
                a1 = x1
                b1 = y1
            }
            
            // 计算右上角
            if x2 > a2 || y2 > b2 {
                a2 = x2
                b2 = y2
            }
            
            // 计算面积
            area += (x2 - x1) * (y2 - y1)
            
            // 记录每个顶点出现的次数
            record(x1, y1)
            record(x1, y2)
            record(x2, y1)
            record(x2, y2)
        }
        
        // 通过左下角和右上角坐标可以算出总面积
        let totalArea = (a2 - a1) * (b2 - b1)
        
        // 如果两个面积不相等，直接返回false
        if area != totalArea {
            return false
        }
        
        // 四个为1的顶点正好是大矩形的四个顶点
        return set.count == 4 && set.contains(key(a1, b1)) && set.contains(key(a1, b2)) && set.contains(key(a2, b1)) && set.contains(key(a2, b2))
    }