单链表与双链表
做面试题时,我们常用的实现方式是
struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
下面讲的主要是用数组来模拟链表。这种实现链表的方式也叫静态链表。
1.单链表
e[N]用来表示某个点的值是多少
ne[N]用来表示某个点的next指针是多少
e和ne是用下标关联起来的
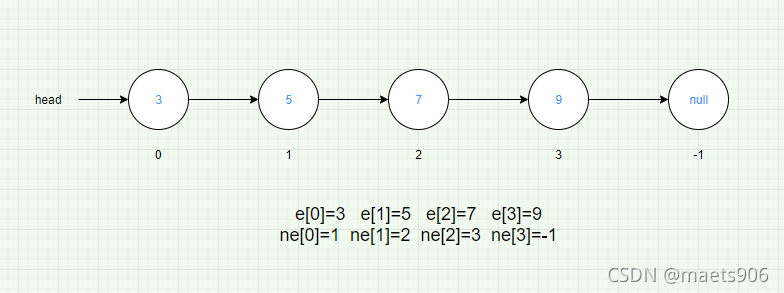
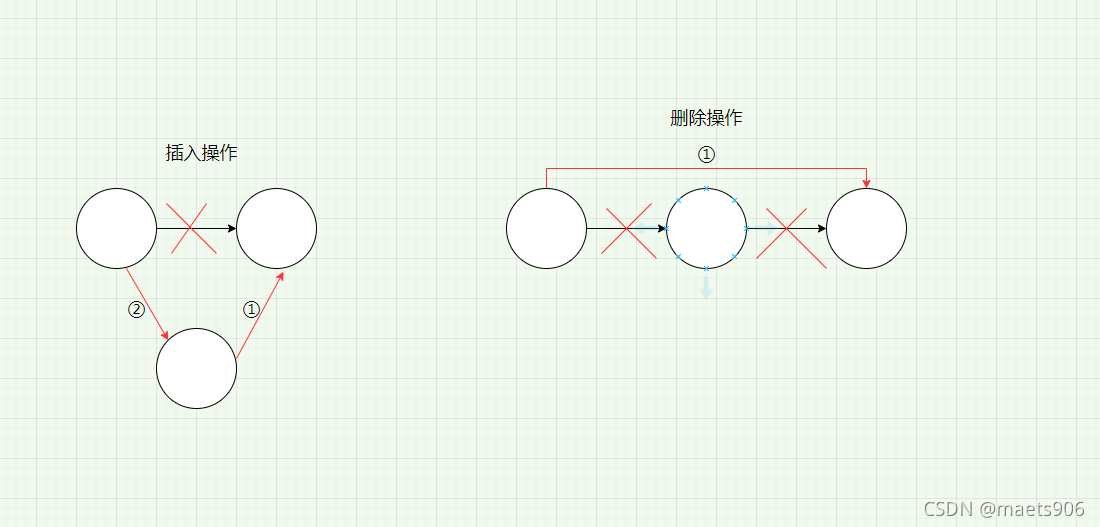
AcWing 826. 单链表
#include <iostream>
using namespace std;
const int N=100010;
/*head 表示头结点的下标
e[i] 表示结点i的值
ne[i] 表示结点i的next指针是多少
idx 存储当前已经用到了哪个点*/
int head,idx,e[N],ne[N];
void init(){
head=-1;
idx=0;
}
//头插
void insert_before_head(int val){
e[idx]=val;
ne[idx]=head;
head=idx;
idx++;
}
void insert_after_k(int k,int val){
e[idx]=val;
ne[idx]=ne[k];
ne[k]=idx;
idx++;
}
void remove(int k){
ne[k]=ne[ne[k]];
}
int main(){
int m;
cin>>m;
init();
while(m--){
int k,x;
char op;
cin>>op;
if(op=='H'){
cin>>x;
insert_before_head(x);
}else if(op=='I'){
cin>>k>>x;
insert_after_k(k-1,x);
}else{
cin>>k;
if(k==0) head=ne[head];
else remove(k-1);
}
}
for(int i=head;i!=-1;i=ne[i]) cout<<e[i]<<" ";
cout<<endl;
return 0;
}
2.双链表
e[N]:当前结点的值是多少
l[N]:当前结点左边是谁
r[N]:当前结点右边是谁
AcWing 827. 双链表
#include <iostream>
using namespace std;
const int N=100010;
int idx,e[N],l[N],r[N];
void init(){
//0表示左端点
//1表示右端点
//虚拟头和虚拟尾
l[0]=-1,r[0]=1,l[1]=0,r[1]=-1;
idx=2;
}
//最左端插入
void insertLeft(int x){
e[idx]=x;
r[idx]=r[0];
l[idx]=0;
l[r[0]]=idx;
r[0]=idx;
idx++;
}
//最右端插入
void insertRight(int x){
e[idx]=x;
r[idx]=1;
l[idx]=l[1];
r[l[1]]=idx;
l[1]=idx;
idx++;
}
void insert_left_k(int k,int x){
e[idx]=x;
r[idx]=k;
l[idx]=l[k];
r[l[k]]=idx;
l[k]=idx;
idx++;
}
void insert_right_k(int k,int x){
e[idx]=x;
r[idx]=r[k];
l[idx]=k;
l[r[k]]=idx;
r[k]=idx;
idx++;
}
//删除第k个插入点
void remove(int k){
l[r[k]]=l[k];
r[l[k]]=r[k];
}
int main(){
int m;
cin>>m;
init();
int k,x;
string s;
while(m--){
cin>>s;
if(s[0]=='L'){
cin>>x;
insertLeft(x);
}else if(s[0]=='R'){
cin>>x;
insertRight(x);
}else if(s[0]=='D'){
cin>>k;
remove(k+1);
}else if(s[0]=='I' && s[1]=='L'){
cin>>k>>x;
insert_left_k(k+1,x);
}else{
cin>>k>>x;
insert_right_k(k+1,x);
}
}
for(int i=r[0];i!=1;i=r[i]) cout<<e[i]<<" ";
cout<<endl;
return 0;
}
栈和队列
栈:后进先出
队列:先进先出
AcWing 828. 模拟栈
#include <iostream>
using namespace std;
const int N=100010;
//tt是栈顶指针
int stk[N],tt;
void push(int x){
stk[tt]=x;
tt++;
}
void pop(){
tt--;
}
bool empty(){
if(tt==0) return true;
else return false;
}
int query(){
if(!empty()) return stk[tt-1];
}
int main(){
tt=0;
int m;
cin>>m;
string s;
int x;
while(m--){
cin>>s;
if(s=="push"){
cin>>x;
push(x);
}else if(s=="pop"){
pop();
}else if(s=="empty"){
bool tmp=empty();
if(tmp) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}else{
cout<<query()<<endl;
}
}
return 0;
}
AcWing 829. 模拟队列
#include <iostream>
using namespace std;
const int N=100010;
//tail指向最后一个元素的下一位
int head,tail,queue[N];
bool isFull(){
return tail+1==head;
}
void push(int x){
if(!isFull()){
queue[tail]=x;
tail++;
}
}
bool empty(){
return tail-head==0;
}
void pop(){
if(!empty()){
head++;
}
}
int query(){
if(!empty()) return queue[head];
}
int main(){
head=0,tail=0;
int m;
cin>>m;
string s;
int x;
while(m--){
cin>>s;
if(s=="push"){
cin>>x;
push(x);
}else if(s=="pop"){
pop();
}else if(s=="empty"){
bool tmp=empty();
if(tmp) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}else{
cout<<query()<<endl;
}
}
return 0;
}
单调栈
单调栈:给定一个序列,求序列中的每一个数左边离它最近的且比它小的数在什么地方
AcWing 830. 单调栈
//暴力做法
for(int i=0;i<n;i++){
for(int j=i-1;j>=0;j--){
if(a[i]>a[j]){
cout<<a[j]<<endl;
break;
}
}
}
我们可以用一个栈把a[i]之前的所有元素存起来
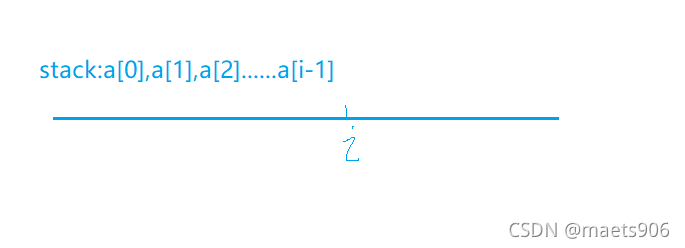
在这个栈里,有些元素永远不会被输出出来,我们就可以将它们删掉。
例如,a[3]>a[5],显然,a[5]在a[3]的右边,距离a[i]更近。我们寻找的是一个数左边离它最近的且比它小的数,那么我们将会找到a[5]而永远不会找到a[3]
当我们把所有a[x]>=a[y]的a[x]删掉后,我们最后剩下的栈一定是单调递增的。
我们再从单调栈的栈顶元素开始查找,如果栈顶元素大于等于a[i],那么我们将其删掉,直到栈顶元素小于a[i],我们将其作为答案输出,并把a[i]放进栈中。
(因为a[i]虽然是用来查找的,但同时也是a[i+1]前面的元素。如果单调栈里的一些元素大于等于被查找的a[i],那么在查找a[i+1]的左边最近的且比a[i+1]小的数时永远不会找到这些大于等于a[i]的元素)
#include <iostream>
using namespace std;
const int N=100010;
int stk[N],tt;
int main(){
int n;
scanf("%d",&n);
while(n--){
int x;
scanf("%d",&x);
while(tt && stk[tt]>=x) tt--;
if(tt){
cout<<stk[tt]<<" ";
stk[++tt]=x;
}else{
cout<<-1<<" ";
stk[++tt]=x;
}
}
return 0;
}
单调队列
主要用途:求滑动窗口里的最大值或最小值
AcWing 154. 滑动窗口

我们随着窗口的移动,每次在队尾插入新元素,同时在队头弹出已经不在窗口里的元素,始终保证队列的长度等于窗口里元素的个数。
暴力做法就是遍历整个队列,找到最小值。
我们下面来思考一下如何优化。
只要队列里有前面一个数比后面一个数大,那前面的那个数就完全没有用。我们把所有在前面的大的数删掉后,整个序列就是一个单调递增的序列。在单调递增的序列里找最小值只需要找最左边的端点,即队头。
找最大值的做法和上面找最小值的做法类似,只需稍作修改。
#include <iostream>
using namespace std;
const int N=1000010;
//q[N]里存的是下标
int n,k;
int a[N],q[N];
int main(){
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
int head=0,tail=-1;
for(int i=0;i<n;i++){
//判断队头是否已经滑出窗口
if(head<=tail && q[head]<i-k+1) head++;
while(head<=tail && a[q[tail]]>=a[i]) tail--;
q[++tail]=i;
if(i>=k-1) printf("%d ",a[q[head]]);
}
printf("\n");
head=0,tail=-1;
for(int i=0;i<n;i++){
if(head<=tail && q[head]<i-k+1) head++;
while(head<=tail && a[q[tail]]<=a[i]) tail--;
q[++tail]=i;
if(i>=k-1) printf("%d ",a[q[head]]);
}
printf("\n");
return 0;
}
KMP
AcWing 831. KMP字符串
对KMP算法的详细解释在下面这篇博客里~
这道题与一般的KMP算法有所不同,需要求出模式串P在母串S中所有出现的位置的起始下标。
我们采用找到结果就输出,并让j指针回溯的方法。
#include <iostream>
using namespace std;
int n,m;
void getNext(string &p,int next[]){
next[0]=0;
int x=0,y=1;
while(y<p.size()){
if(p[x]==p[y]){
next[y]=x+1;
x++;
y++;
}else if(p[x]!=p[y] && x==0){
next[y]=0;
y++;
}else{
x=next[x-1];
}
}
return;
}
void kmp(string &t,string &p){
int i=0,j=0;
int next[p.size()];
getNext(p,next);
while(i<t.size() && j<p.size()){
if(t[i]==p[j]){
i++;
j++;
}else{
if(j!=0) j=next[j-1];
else i++;
}
if(j==p.size()){
printf("%d ",i-j);
if(j!=0) j=next[j-1];
}
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n;
string p;
cin>>p;
cin>>m;
string t;
cin>>t;
kmp(t,p);
return 0;
}