Huffman树与Huffman编码
问题描述
已知某系统在通信联络中只可能出现6种字符,其使用频度如下表所示:

根据Huffman编码原理,为6种字符设计一种Huffman编码方案。
算法分析与设计
(1)Huffman算法
①根据给定的n个权值{w1,w2,…,wn}构造n棵二叉树的集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树均空。
②在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
③在F中删除这两棵树,同时将新得到的二叉树加入F中。
④重复②、③,直到F中只含一棵树为止。这棵树便是Huffman树。
(2)求Huffman编码算法
①根据给定的一组权值构造一棵Huffman树,由此得到的二进制前缀便为Huffman编码。由于Huffman树没有度为1的结点,则一棵有n个叶子结点的Huffman树共有2n-1个结点,设计一个结构数组,存储2n-1个结点的值,包括结点值、权重、父结点、左孩子和右孩子等。
②根据第1步构造出的Huffman树,求出每一个字符的Huffman编码,数据保存在一个字符串数组中。其方法是,从每一个叶子结点出发向根结点搜索,若遇左分支代码取’0’,若遇右分支,代码取’1’。
③输出各字符的Huffman编码。
参考程序
#include <stdio.h>
#include <string.h>
#define MAX 21
typedef struct
{ // 定义Huffman树结点结构
char data; // 结点值
int weight; // 权重
int parent; // 父结点
int lchild; // 左孩子
int rchild; // 右孩子
} HTNode;
typedef struct
{ // 定义Huffman编码结构
char cd[MAX];
int start;
} HCode;
void CreatHT(HTNode *HT, int n)
{
int i, k, l, r;
int m1, m2;
int lnode, rnode;
for (i = 1; i < 2 * n; i++)
HT[i].parent = HT[i].lchild = HT[i].rchild = NULL; // 初始化
for (i = n + 1; i < 2 * n; i++)
{ // 构造Huffman树
m1 = m2 = 0x7fff; // m1取最小权重,m2取次小权重
lnode = rnode = 0; // lnode, rnode分别取两个最小权重的结点位置
for (k = 1; k < i; k++)
{
if (HT[k].parent == 0)
{
if (HT[k].weight < m1)
{
m2 = m1;
rnode = lnode;
m1 = HT[k].weight;
lnode = k;
}
else if (HT[k].weight < m2)
{
m2 = HT[k].weight;
rnode = k;
}
}
}
HT[lnode].parent = i;
HT[rnode].parent = i;
HT[i].weight = m1 + m2;
HT[i].lchild = lnode;
HT[i].rchild = rnode;
}
}
void CreatHCode(HTNode *HT, HCode *hcd, int n)
{
int i, f, c;
HCode hc;
for (i = 1; i <= n; i++)
{
hc.start = n;
c = i;
f = HT[i].parent;
while (f != 0)
{
if (c == HT[f].lchild) // c是f的左孩子,编码取'0',否则取'1'
hc.cd[--hc.start] = '0';
else
hc.cd[--hc.start] = '1';
c = f; // 向根结点方向搜索
f = HT[c].parent;
}
hcd[i] = hc;
}
}
void PrintHCode(HTNode *HT, HCode *hcd, int n)
{
int i, k;
for (i = 1; i <= n; i++)
{
printf(" %c:", HT[i].data);
for (k = hcd[i].start; k < n; k++)
printf("%c", hcd[i].cd[k]);
printf("\n");
}
}
void Unziped(HTNode *HT)
{
int i = 0;
int length;
char ch[30];
scanf("%s", ch);
length = strlen(ch);
while (i != length)
{
if (ch[i] == '0')
printf("%c", HT[i + 1].data);
else
printf("%c", HT[i + 1].data);
i++;
}
}
int main()
{
int i, n;
HTNode HT[2 * MAX - 1];
HCode hcd[MAX];
printf("(1)创建Huffman树......\n");
do
{
printf(" 请输入元素个数(1-%d):", MAX - 1);
scanf("%d", &n);
} while (n < 1 || n > MAX - 1); // 确保n值合规
for (i = 1; i <= n; i++)
{ // Huffman树结点存放在ht数组从1下标开始的位置
fflush(stdin);
printf(" 第%d个元素的结点值==>", i);
scanf("%c", &HT[i].data);
printf("\t权重==>");
scanf("%d", &HT[i].weight);
}
CreatHT(HT, n);
printf(" Huffman树创建成功!\n");
fflush(stdin);
getchar();
printf("(2)创建Huffman编码......\n");
CreatHCode(HT, hcd, n);
printf(" Huffman编码创建成功!\n");
getchar();
printf("(3)输出Huffman编码:\n");
PrintHCode(HT, hcd, n);
printf("(4)请输入电文:\n");
Unziped(HT);
return 0;
}
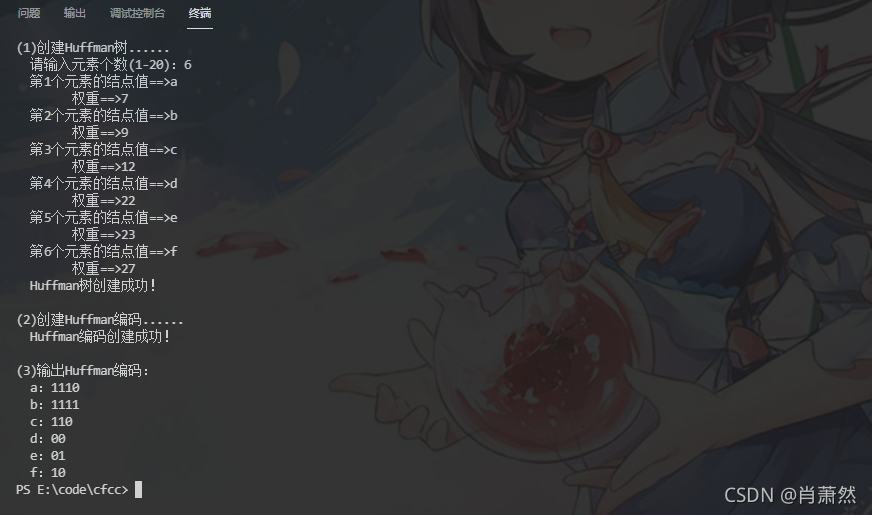
测试数据及测试结果