[数据结构与算法]中序线索二叉树的实现(源代码以及讲解)

概念

??传统的使用二叉链表实现的二叉树由于会有n+1个空间没有使用上，因此我们可以在该二叉树上使用其没有使用的空指针域，让这些指针域指向该节点的前驱或后继节点，以实现空间最大利用率，同时这种新的二叉树在需要知道某个之间的前驱或后继节点也更加的方便自如，那么这种二叉树就叫做—线索二叉树，我们规定，如果某个节点的左孩子为空，则其左孩子的指针域改为指向其前驱节点，如若右孩子为空，那么右孩子的指针域指向该节点的后继节点。

实例

先对这棵树中序遍历，之后就可以知道每一个结点的前驱和后继节点了。
然后根据上面的规则我们就能得到一个新的二叉树。

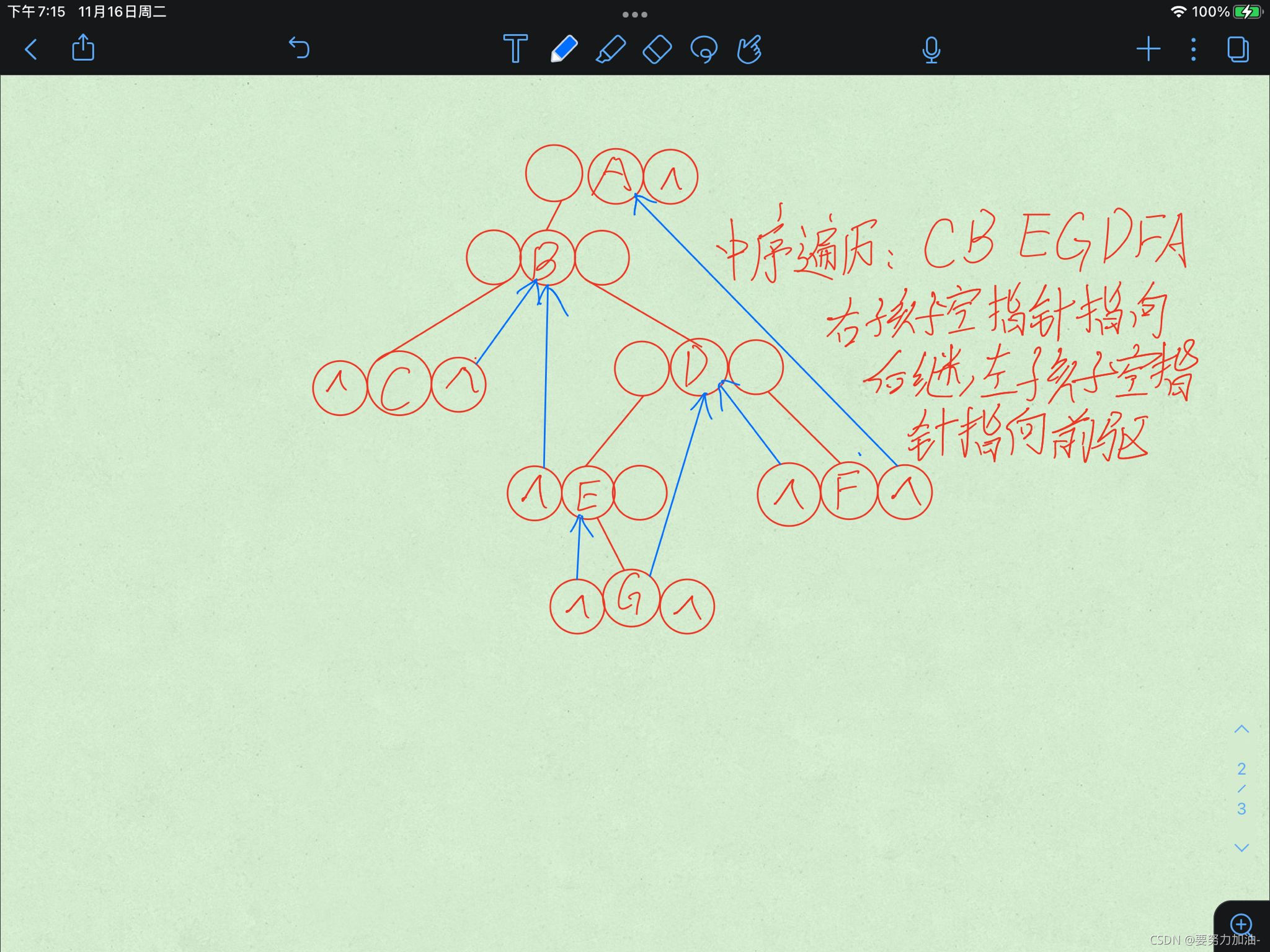
当然，你可能会发现，如果这样子那么基本每一个节点的左右孩子都不是空的，那么我如何知道这个结点指向的到底是前驱还是后继指针还是我的孩子呢？
因此，我们需要在二叉树的每一个结点补上一个标志域Ltag和Rtag。
并且规定：
????Ltag=0代表的是左孩子
????Ltag=1代表的是前驱结点
????Rtag=0代表的是右孩子
????Rtag=1代表的是后继结点

代码以及实现思想

以文件内的这棵树为例(可能字迹有点丑)
笔记，免积分下载

先输入如图的二叉树，以中序遍历的情况可以得到DBEAC

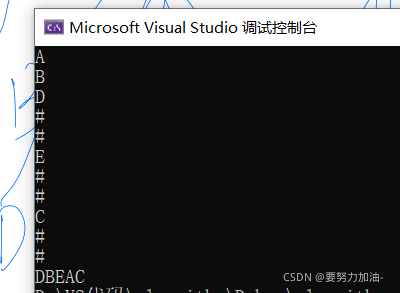
那么如何可以做到这种效果？
1:构建二叉树
首先输入一个要插入的每一个元素，如果其子树为空，则输入#结束
其数据分为左右标记位，指针域，数据域

typedef struct ThreadTreeNode {
	char data; 						//数据域 
	struct ThreadTreeNode* lchild;  //左孩子指针域 
	struct ThreadTreeNode* rchild;  //右孩子指针域 
	int LTag;			//左标志位 0 1 
	int RTag;				//右标志位 0 1 
}Tnode, * Ttree;


void CreateBinaryTree(Ttree& T)
{
	char ch;
	cin >> ch;
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		if (!(T = (Tnode*)malloc(sizeof(Tnode))))  exit(0);
		//这里注意正确输入的顺序 
		T->data = ch;
		T->LTag = Link;			 //初始化设定左右子树为指针类型
		T->RTag = Link;
		CreateBinaryTree(T->lchild); //先构造左子树 
		CreateBinaryTree(T->rchild); //再构造右子树 
	}
}

2：中序遍历的方式线索化二叉树
先创建一个头节点Thrt，这个头节点用于指向二叉树的根节点
同时二叉树的最后一个结点的右孩子指向该头节点，形成一个闭环
首先令该头节点的右孩子指向自己(暂时)，令左孩子指向二叉树的根节点
之后调用线索化函数void TheadBinaryTree(Ttree p),线索化该二叉树，线索化思想为先找到最左的结点，如果该最左的左孩子为空(最左自然为空)，那么我们将其左孩子指向该节点的前驱结点(如果这个结点本身就是第一个结点，那么让他指向头结点)，之后右结点也通过递归的方法，传入当前结点§，pre结点此时指向的以及是前一个结点，那么之后只要pre的右结点令其指向当前传入的结点§,那么就可以将前一个访问的结点的右孩子设置为其后驱结点，如此往复，线索化成功

//先创建头指针让头指针指向二叉树
//之后以中序遍历的方法线索化该二叉树
void InOrderTheadBTree(Ttree& Thrt, Ttree T)
{
	//创建头结点Thrt 
	if (!((Thrt) = (Ttree)malloc(sizeof(Tnode)))) 
	{
		exit(0);
	}
	Thrt->LTag = Link;			//头结点的左标志位为0，指针 
	Thrt->RTag = Thead;			//头结点的右标志位为1，线索 
	Thrt->rchild = Thrt;  		//右指针回指本身
	if (!T) 
	{
		Thrt->lchild = Thrt;  //二叉树为空时，指向为无，回指本身 
	}
	else
	{
		//若二叉树存在，将头结点与二叉树进行相应的链接
		Thrt->lchild = T;       //让头指针指向二叉树T(T中存放的是之前输入的二叉树)
		pre = Thrt;				//头结点为前驱 
		TheadBinaryTree(T);		    //中序遍历进行中序线索化
		pre->rchild = Thrt;		//右指针回指本身 
		pre->RTag = Thead;		//右标记位设置为线索
		Thrt->rchild = pre;	
	}
}
//线索化的函数
void TheadBinaryTree(Ttree p)
{
	if (p)
	{
		TheadBinaryTree(p->lchild);
		if (!p->lchild)   //左指针域为空则线索化 
		{
			p->LTag = Thead;
			p->lchild = pre;
		}
		if (!pre->rchild)
		{
			pre->RTag = Thead;
			pre->rchild = p;
		}
		pre = p;
		TheadBinaryTree(p->rchild);
	}
}

3：中序遍历线索二叉树
类似于中序遍历，先将指针指向最左的结点，输出该节点之后通过访问右孩子的方式(因为右孩子一定是后继结点)就可以遍历整棵线索二叉树，比较好理解

//中序遍历这个二叉树
void InOrderTraverse(Ttree Thrt)
{
	Ttree p;
	//T指向头结点，p指向根结点 
	p = Thrt->lchild;
	while (p != Thrt)   //若p==T，则遍历完成，再次回到头结点 
	{
		while (p->LTag == Link) //找到左节点
		{
			p = p->lchild;		//直到找到根结点的最左子树的最左结点 
		}
		cout << p->data;        //找到了最左边的结点，输出
		while (p->RTag == Thead && p->rchild != Thrt)//线索化完成 此时左节点的右节点应该是后驱结点
		{ 
			p = p->rchild;		 //指向后驱结点
			cout << p->data;	 //输出后驱结点
		}
		p = p->rchild;			 //访问该结点的右结点
	}
}

4：源代码

#pragma once
#include<iostream>
#include <cstdio>
#include<cstdlib>
typedef int Status;
typedef int ElemType;
typedef char cElemType;
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAXSIZE 20
#define make (struct student*)malloc(sizeof(struct student));
using namespace std;

enum Tag{Link,Thead};
//Ptr=0:指针，Thread=1：线索 

//二叉链表的结点结构 
typedef struct ThreadTreeNode {
	char data; 						//数据域 
	struct ThreadTreeNode* lchild;  //左孩子指针域 
	struct ThreadTreeNode* rchild;  //右孩子指针域 
	int LTag;			//左标志位 0 1 
	int RTag;				//右标志位 0 1 
}Tnode, * Ttree;

Ttree pre;  //指向刚刚访问过的结点  是一个指针类型

void CreateBinaryTree(Ttree& T);				  //创建二叉树
void InOrderTheadBTree(Ttree& Thrt, Ttree T); //以中序的方法线索化二叉树
void TheadBinaryTree(Ttree p);		 			  //二叉树的线索化函数
void InOrderTraverse(Ttree Thrt);		      //中序遍历二叉树

void CreateBinaryTree(Ttree& T)
{
	char ch;
	cin >> ch;
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		if (!(T = (Tnode*)malloc(sizeof(Tnode))))  exit(0);
		//这里注意正确输入的顺序 
		T->data = ch;
		T->LTag = Link;			 //初始化设定左右子树为指针类型
		T->RTag = Link;
		CreateBinaryTree(T->lchild); //先构造左子树 
		CreateBinaryTree(T->rchild); //再构造右子树 
	}
}
//中序遍历这个二叉树
void InOrderTraverse(Ttree Thrt)
{
	Ttree p;
	//T指向头结点，p指向根结点 
	p = Thrt->lchild;
	while (p != Thrt)   //若p==T，则遍历完成，再次回到头结点 
	{
		while (p->LTag == Link) //找到左节点
		{
			p = p->lchild;		//直到找到根结点的最左子树的最左结点 
		}
		cout << p->data;        //找到了最左边的结点，输出
		while (p->RTag == Thead && p->rchild != Thrt)//线索化完成 此时左节点的右节点应该是后驱结点
		{ 
			p = p->rchild;		 //指向后驱结点
			cout << p->data;	 //输出后驱结点
		}
		p = p->rchild;			 //访问该结点的右结点
	}
}
//先创建头指针让头指针指向二叉树
//之后以中序遍历的方法线索化该二叉树
void InOrderTheadBTree(Ttree& Thrt, Ttree T)
{
	//创建头结点Thrt 
	if (!((Thrt) = (Ttree)malloc(sizeof(Tnode)))) 
	{
		exit(0);
	}
	Thrt->LTag = Link;			//头结点的左标志位为0，指针 
	Thrt->RTag = Thead;			//头结点的右标志位为1，线索 
	Thrt->rchild = Thrt;  		//右指针回指本身
	if (!T) 
	{
		Thrt->lchild = Thrt;  //二叉树为空时，指向为无，回指本身 
	}
	else
	{
		//若二叉树存在，将头结点与二叉树进行相应的链接
		Thrt->lchild = T;       //让头指针指向二叉树T(T中存放的是之前输入的二叉树)
		pre = Thrt;				//头结点为前驱 
		TheadBinaryTree(T);		    //中序遍历进行中序线索化
		pre->rchild = Thrt;		//右指针回指本身 
		pre->RTag = Thead;		//右标记位设置为线索
		Thrt->rchild = pre;	
	}
}
//线索化的函数
void TheadBinaryTree(Ttree p)
{
	if (p)
	{
		TheadBinaryTree(p->lchild);
		if (!p->lchild)   //左指针域为空则线索化 
		{
			p->LTag = Thead;
			p->lchild = pre;
		}
		if (!pre->rchild)
		{
			pre->RTag = Thead;
			pre->rchild = p;
		}
		pre = p;
		TheadBinaryTree(p->rchild);
	}
}

int main()
{
	Ttree Thrt,T;				//头结点 
	CreateBinaryTree(T);		//建立二叉树
	InOrderTheadBTree(Thrt, T);		//让头结点指向根节点，并且线索化该根结点对应的二叉树
	InOrderTraverse(Thrt);			//中序遍历线索二叉
}