图的存储结构
G = ( V , E ) G=(V,E) G=(V,E) V V V表示顶点集合, E E E表示边集合
邻接矩阵
是顺序存储结构
邻接矩阵是表示顶点之间相邻关系的矩阵。
设G=(V,E)是具有n(n>0)个顶点的图,顶点的编号依次为0~n-1。
特点
一个图的邻接矩阵表示是唯一的。
特别适合于稠密图的存储。
邻接矩阵的存储空间为O(n2)
不带权图
(1)如果G是无向图,则:
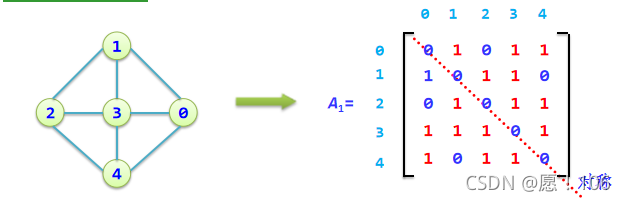
$A[i][j]=1$:若$(i,j)∈E(G)$ 0:其他
解释:
矩阵中,0-1-2-3-4分别代表图中各个点,横纵坐标都是代表各个顶点。
对于 A i A_i Ai?这个矩阵,如果第 A [ i ] [ j ] = = 1 A[i][j]==1 A[i][j]==1,那么在无向图中 ( i , j ) (i,j) (i,j)这条边一定存在。
(2)如果G是有向图,则:
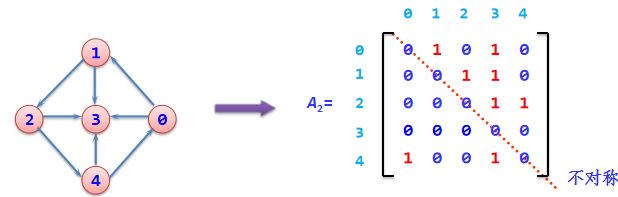
? A [ i ] [ j ] = 1 A[i][j]=1 A[i][j]=1:若 < i , j > ∈ E ( G ) <i,j>∈E(G) <i,j>∈E(G) 0:其他
对于 A i A_i Ai?这个矩阵,如果第 A [ i ] [ j ] = = 1 A[i][j]==1 A[i][j]==1,那么在无向图中 < i , j > <i,j> <i,j>这条边一定存在。
(3)如果G是带权无向图,则:
用每个点存储权重
? A [ i ] [ j ] = w i j A[i][j]= w_{ij} A[i][j]=wij? :若 i ≠ j i≠j i?=j且(i,j)∈E(G) $ 0:i=j$ ∞ ∞ ∞:其他
(4)如果G是带权有向图,则:
用每个点存储权重
? $ A[i][j]= w_{ij}$ :若{i≠j}且 < i , j > ∈ E ( G ) <i,j>∈E(G) <i,j>∈E(G) 0 : i = j 0:i=j 0:i=j ∞ ∞ ∞:其他
代码
#define MAXV <最大顶点个数> //#define 是宏定义
typedef struct //这个结构体定义,每个顶点的信息。
{ int no; //顶点编号
InfoType info; //顶点其他信息,* InfoType 这个不是类型,需要自己定义,你可以存一个字符串,数组,一个数字都可以,都表示这个顶点的信息。
} VertexType;
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
邻接表存储方法
特别适合于稀疏图存储。
邻接表表示不唯一。
邻接表的存储空间为O(n+e)
定义
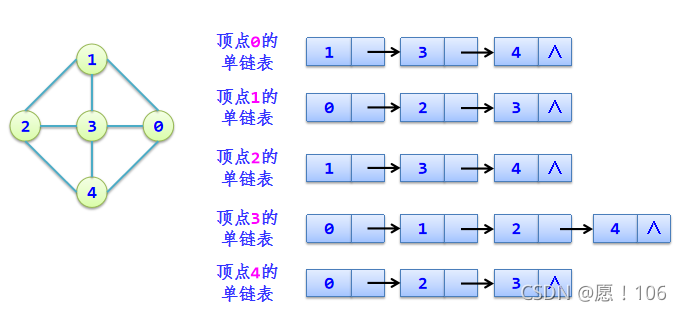
step1:
对图中每个顶点i建立一个单链表,将顶点
i
i
i的所有直接相邻接点链起来。
step2:
每个单链表上添加一个表头结点(表示顶点信息)。并将所有表头结点构成一个数组,下标为 i i i的元素表示顶点 i i i的表头结点。
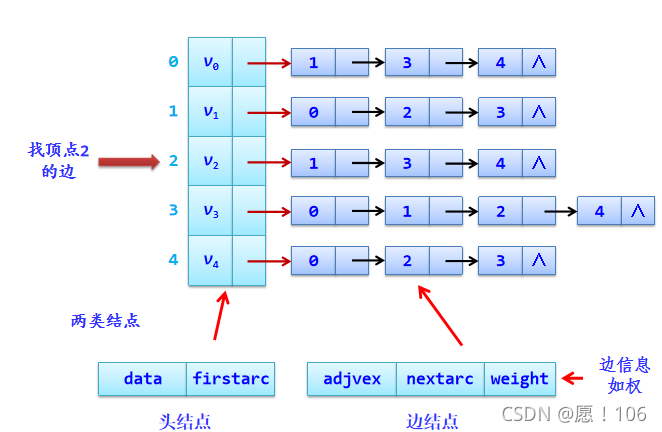
图的邻接表是 顺序分配?链式分配
我们从头节点找对应的顶点,在边节找到点中存储信息。
实例
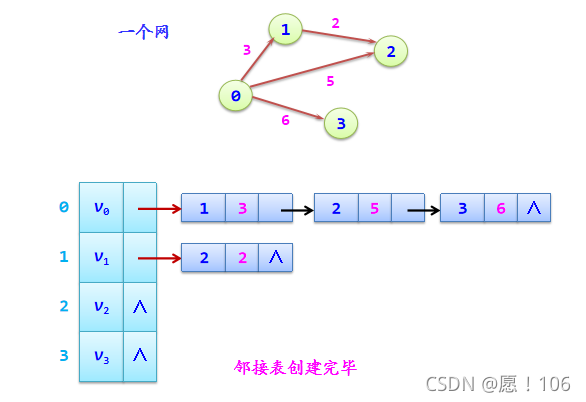
对于2、3顶点他们没有后续节点,所以不是指向的为空,而是这个头节点存储为空
代码
typedef struct ANode//链节点
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType weight; //该边的权值等信息
} ArcNode;
typedef struct Vnode//头节点
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{ VNode adjlist[MAXV]; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
### 空间资源对比
当图是稠密图时,边非常多,每个点对应的边也非常多。 O ( n + e ) O(n+e) O(n+e)中 e甚至会到达 e = n ? ( n ? 1 ) e=n*(n-1) e=n?(n?1)的空间,而邻接表始终是 O ( n 2 ) O(n^2) O(n2)
当图是稀疏图时,边很少,邻接表对应 O ( n 2 ) O(n^2) O(n2)中存在很多0,造成空间浪费,而稠密图 O ( n + e ) O(n+e) O(n+e)中 e很小,甚至最小可以到达0
- 如有疑问:请前往http://www.i5201314.top留言咨询
- 请收藏,避免迷路。