在了解学习堆排序之前,我们必须清楚以下的概念:

?上述概念搞清楚之后,来看下面的原理图:
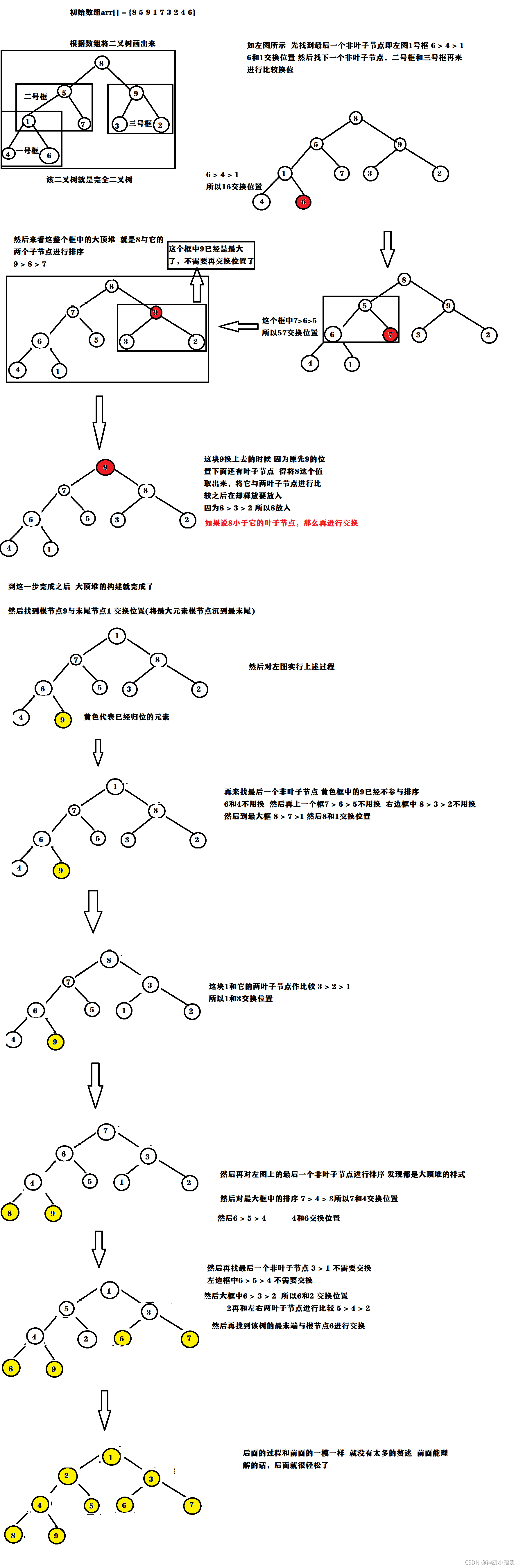
?然后原理部分就讲完了
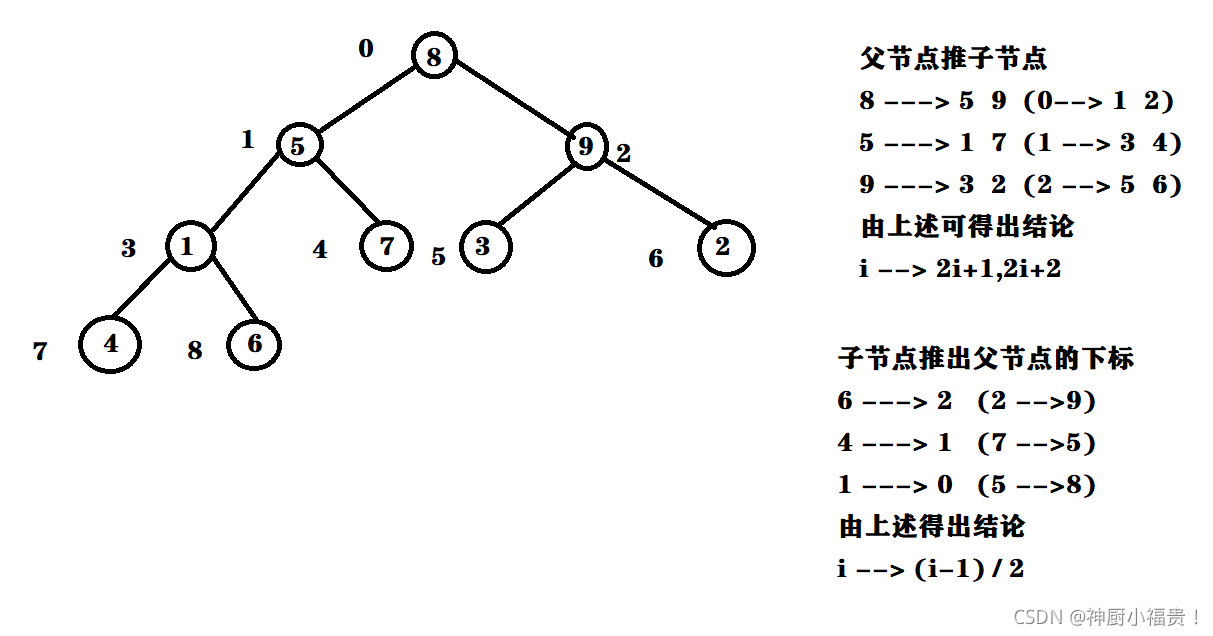
下面来看如何由子节点下标推出父节点和父节点下标推出子节点下标
?
下面这个原理图来展现一下为什么在调整大顶堆的时候 要将下标给到len-1最大值
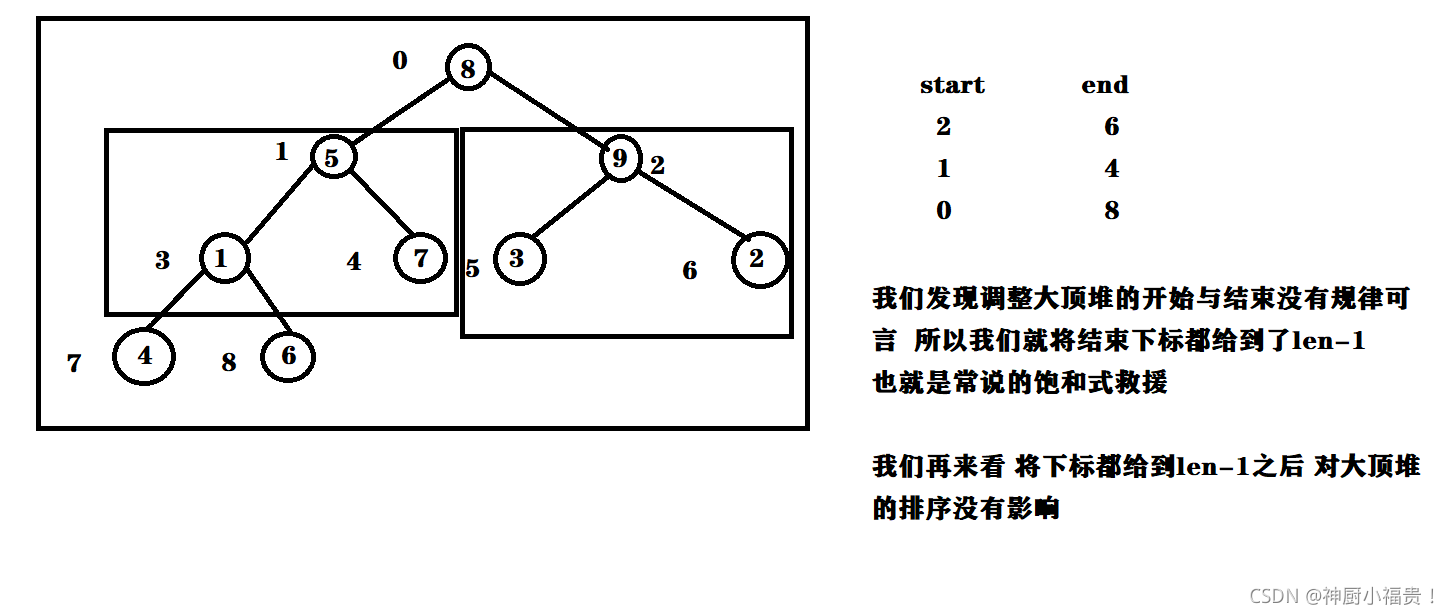
?
?所有的前期任务完成了之后,下面进行代码实现:
//该函数是用来调整大顶堆的
void AdjustHeap(int* arr, int start, int end)
{
int tmp = arr[start];
int i = start;
int j = 2*i + 1; //j指向两子下标中较大那个值 那么就先指向2i+1 让下面再做个比较
for (j; j <= end; j = 2*i + 1)
{
if (j<end && arr[j + 1]>arr[j]) //如果子节点的右值大于左值 则将j指向右值
{
j++;
}
if (arr[j] > tmp) //如果子节点的值大于tmp的值 那么将arr[start] = arr[j] 又因为i = start
{
arr[i] = arr[j];
i = j;
}
else
{
break; //当arr[j]就是最大值且arr[j] < tmp 那么break掉 直接将tmp
}
}
arr[i] = tmp;
}
void HeapSort(int* arr, int len)
{
//这块寻找最后一个非叶子节点的下标 len-1为最后一个叶子节点的下标 而由上图可以得出子下标推父节点的公式
for (int i = ((len - 1) - 1) / 2; i >= 0; i--)
{
AdjustHeap(arr, i, len - 1); //i就是大顶堆开始的下标 也就是叶子节点的父节点
//len-1就是下标为i的父节点调整大顶堆的结束位置 这块为什么要给len-1呢 在上图中给出了明确的解释
}
//上述执行完之后 初始状态下第一次最难的排序就完成了
//下面为交换函数
for (int i = 0; i < len - 1 ; i++)
{
int tmp = arr[0];
arr[0] = arr[len - 1 - i];
arr[len - i - 1] = tmp;
AdjustHeap(arr, 0, (len - 1 - i) - 1); //这块的(len-1-i) - 1的意思就是将排序完的数就不再参与排序 上述原理图上面有说到的
}
}下面附上主函数以及运行截图:
?
int main()
{
int arr[] = { 8,5,9,1,7,3,2,4,6 };
int len = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr, len);
show(arr, len);
return 0;
}
?