[数据结构与算法]java数据结构与算法（二叉排序树【BST】，平衡二叉树【AVL】）

二叉排序树（BST）

二叉排序树BST（Binary Sort Tree）：对于二叉树的任何一个非叶子结点，要求左子节点的值比当前结点的值小，右子节点的值比当前结点的值大。
特别说明：如果右相同的值，可以将该结点放在左子节点或右子节点

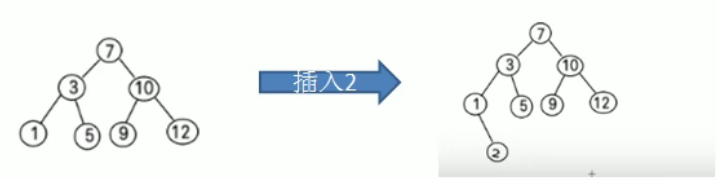
创建和遍历

’首先实现二叉排序树的创建和遍历；
二叉排序树的创建和之前学过的二叉树的创建差不多，只是在插入结点的时候多了一个判断条件，需要根据插入结点和原先二叉排序树的结点进行比较找到插入的位置
关于遍历：这里我们代码实现的是中序遍历，对于二叉排序树来说，中序遍历恰好输出的是该组数据从小到大的排列序列
代码实现：

//创建一棵二叉排序树
class createBinaryTree {
    private binaryNode root;

    //添加结点
    public void add(binaryNode node) {
        if(root == null) {
            root = node;
            return ;
        }
        root.add(node);
    }
    //二叉排序树的中序遍历
    public void infixOrder() {
        if(root == null) {
            System.out.println("这棵二叉排序树是空的");
            return;
        }
        root.infixOrder();
    }
}

//创建二叉排序树的结点
class binaryNode{
    int value;
    binaryNode left;
    binaryNode right;
    public binaryNode(int value) {
        this.value = value;
    }
    public String toString() {
        return "[value=" + value + "]";
    }
    //二叉排序树中序遍历
    public void infixOrder() {
        if(this == null) return ;
        if(this.left != null)
            this.left.infixOrder();
        System.out.println(this);
        if(this.right != null)
            this.right.infixOrder();
    }

    //二叉排序树添加结点
    public void add(binaryNode node) {
        if(this == null) return ;
        if(node.value < this.value) { //如果添加结点的值比此结点的值小就往他的左边插
            if(this.left != null)
                this.left.add(node);
            else
                this.left = node;
        } else { //如果添加结点的值比此结点的值大，就往此节点的右子节点插
            if(this.right != null)
                this.right.add(node);
            else
                this.right = node;
        }
    }
}

删除二叉排序树的结点

删除二叉排序树结点的三种情况以及思路分析：
（1）待删除的结点是叶子结点：找到目标结点（待删除结点）以及目标结点的父节点，直接将其父节点的left或者right至为空（如果目标结点在left则置 left为空，如果目标结点在right则置right为空）
（2）待删除结点是只有一棵子树的结点：找到目标结点以及目标结点的父结点，将原来父亲结点指向目标结点的指针该成指向目标结点的子树；
（3）待删除结点是有两颗子树的结点【该情况有两种方法】:
不推荐方法2，方法2只使用于二叉树层数比较少的情况
方法<1>找到目标结点以及目标结点的父节点，在去找目标结点右子树里值最小的结点temp，并将此结点记录下来，然后将temp删除，在将目标结点的值改为temp即可；
方法<2>找到目标结点以及目标结点的父节点，在去找目标结点左子树里值最大的结点temp，并将此结点记录下来，然后将temp删除，在将目标结点的值改为temp即可；

代码实现:

//创建一棵二叉排序树
class createBinaryTree {
    private binaryNode root;
    //查找目标结点
    public binaryNode targetSearch(int value) {
        if(root == null) return null;
        return root.targetSearch(value);
    }
    //查找目标结点的父节点
    public binaryNode parentSearch(int value) {
        if(root == null || root.value == value) return null;
        return root.parentSearch(value);
    }

    //删除指定结点
    public void delete(int value) {
        //先找到该结点
        binaryNode target = targetSearch(value);
        //找到该节点的父结点
        binaryNode parent = parentSearch(value);
        if(target == null) return ;
        if(target == root && target.right == null &&target.left == null)  {
            root = null;
            return ;
        }

        //删除叶子结点
        if(target.left == null && target.right == null) {
            //判断目标结点是其父结点的左子节点还是右子节点
            if(parent.left == target)
                parent.left = null;
            if(parent.right == target)
                parent.right = null;
        } else if(target.left != null && target.right != null) {//删除有两个子节点的结点
            //找到右子树的最小值，并将其删除
            int min = searchMax(target);
            //将其值赋给target
            target.value = min;

        } else {//删除只有一个子节点的结点
           //判断target是parent的左节点还是右节点
            if(target.left != null) { //如果target是左子节点
                if(parent != null) {//如果是不是根节点那就利用parent删除
                    //判断target的子树是左子树还是右子树
                    if (parent.left == target)
                        parent.left = target.left;
                    else
                        parent.right = target.left;
                } else {//如果是根节点那就直接把root的指针指向他的下一结点
                    root = target.left;
                }
            } else {//如果target是parent的右子节点
                if(parent != null) {
                    //判断target存在的是左子树还是右子树
                    if (parent.left == target)
                        parent.left = target.right;
                    else
                        parent.right = target.right;
                } else {
                    root = target.right;
                }
            }
    }

    //在delete方法中，帮助找到删除存在两个子节点的结点的右子节点的最大值
    public int searchMax(binaryNode node) {
        binaryNode temp = node.right;
        while(true) {
            if(temp.left == null) break;
            temp = temp.left;
        }
        //找到右子树的最小结点，记录下他的值，在把他删除
        int Min = temp.value;
        delete(Min);
        return Min;
    }
}




//创建二叉排序树的结点
class binaryNode{
    int value;
    binaryNode left;
    binaryNode right;
    public binaryNode(int value) {
        this.value = value;
    }
    public String toString() {
        return "[value=" + value + "]";
    }

    //查找要删除的目标结点的父节点
    public binaryNode parentSearch(int value) {
        //在来判断此结点的左孩子,右孩子是不是目标结点，如果是就直接返回此结点
        if((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value))
            return this;
        else {
            //如果此结点的左子节点不为空，并且目标值小于此结点，那么就往左子树进行递归
            if(this.value > value && this.left != null)
                return this.left.parentSearch(value);
            //不往左子节点查找，那么柚子结点符合条件的时候就往右子节点查找
            else if(this.value <= value && this.right != null)
                return this.right.parentSearch(value);
            //以上条件都不满足的时候就说明没有找到
            else
                return null;
        }

    }

    //查找要删除的目标结点
    public binaryNode targetSearch(int value) {
        //如果当前结点就是目标结点，那么就直接返回
        if(this.value  == value) return this;
        //在往此结点的左子节点进行搜索
        else if(value < this.value) {
            if(this.left != null)
                return this.left.targetSearch(value);
            else
                return null;
        }else {//在往此结点的右子节点进行搜索
            if(this.right != null)
                return this.right.targetSearch(value);
            else
                return null;
        }
    }
}

平衡二叉树（AVL树）

平衡二叉树也叫平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树，可以保证查询效率较高。
具有的特点：他是一棵空树或他的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，平衡二叉树的常用实现方法有红黑树，AVL，替罪羊树，treap,伸展树

为什么会出现平衡二叉树呢，就像我们上面讲的二叉排序树，如果我们给他的数列是{1,3，5,7，9,10,12}，那么利用二叉排序树创建出来的树就是这样的：

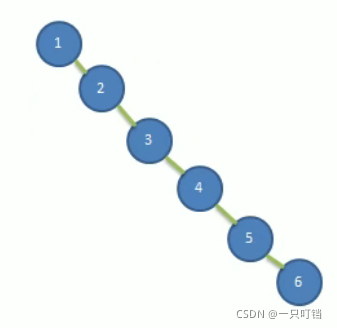
这样的树查询速率可能不会得到提高，反而还会比原来的数列查找更慢，因此，我们就出现了平衡二叉树来解决这样的问题

左旋转

将二叉排序树装换为平衡二叉树的方法：
如果左子树的高度底，右子树的高度高，并且两个左右两边的高度差大于1，那么就用左旋转
步骤：
（1）创建一个新的结点，新结点的值等于当前根节点(root)的值
（2）把新节点的左子树设置为当前结点(root)的左子树
（3）把新结点的右子树设置为当前结点(root)的右子树的左子树
（4）把当前结点(root)的值换为右子节点的值
（5）把当前结点(root)的右子树设置为右子树的右子树
（6）把当前结点（root）的左子树设置为新节点

因为二叉平衡树是在二叉排序树上实现一些功能，因此可以在原来的二叉排序树上进行添加功能即可
代码实现：

//创建二叉排序树的结点
class binaryNode{
    int value;
    binaryNode left;
    binaryNode right;
    public binaryNode(int value) {
        this.value = value;
    }
    public String toString() {
        return "[value=" + value + "]";
    }

    //返回左子树的高度
    public int leftHeight() {
        if(left == null) return 0;
        return left.height();
    }
    //返回右子树的高度
    public int rightHeight() {
        if(right == null) return 0;
        return right.height();
    }

    //返回当前结点的高度
    public int height() {
        return Math.max(left == null ? 0 : left.height(),right == null ? 0 : right.height())+1;
    }

    //左旋转方法
    private void leftRotate() {
        //创建一个新的结点，新结点的值等于当前根节点(root)的值
        binaryNode node = new binaryNode(value);
        //把新节点的左子树设置为当前结点(root)的左子树
        node.left = left;
        //把新结点的右子树设置为当前结点(root)的右子树的左子树
        node.right = right.left;
        //把当前结点(root)的值换为右子节点的值
        value = right.value;
        //把当前结点(root)的右子树设置为右子树的右子树
        right = right.right;
        //把当前结点（root）的左子树设置为新节点
        left = node;
    }
}

右旋转

如果右子树的高度底，左子树的高度高，并且两个左右两边的高度差大于1，那么就用右旋转
步骤：
（1）创建一个新的结点，新结点的值等于当前根节点(root)的值
（2）把新节点的右子树设置为当前结点(root)的右子树
（3）把新结点的左子树设置为当前结点(root)的左子树的右子树
（4）把当前结点(root)的值换为左子节点的值
（5）把当前结点(root)的左子树设置为左子树的左子树
（6）把当前结点（root）的右子树设置为新节点

代码实现：

//创建二叉排序树的结点
class binaryNode{
    int value;
    binaryNode left;
    binaryNode right;
    public binaryNode(int value) {
        this.value = value;
    }
    public String toString() {
        return "[value=" + value + "]";
    }

    //返回左子树的高度
    public int leftHeight() {
        if(left == null) return 0;
        return left.height();
    }
    //返回右子树的高度
    public int rightHeight() {
        if(right == null) return 0;
        return right.height();
    }

    //返回当前结点的高度
    public int height() {
        return Math.max(left == null ? 0 : left.height(),right == null ? 0 : right.height())+1;
    }

    //左旋转方法
    private void leftRotate() {
        //创建一个新的结点，新结点的值等于当前根节点(root)的值
        binaryNode node = new binaryNode(value);
        //把新节点的左子树设置为当前结点(root)的左子树
        node.left = left;
        //把新结点的右子树设置为当前结点(root)的右子树的左子树
        node.right = right.left;
        //把当前结点(root)的值换为右子节点的值
        value = right.value;
        //把当前结点(root)的右子树设置为右子树的右子树
        right = right.right;
        //把当前结点（root）的左子树设置为新节点
        left = node;
    }

    //右旋转方法
    private  void rightRotate() {
        //创建一个新的结点，新结点的值等于当前根节点(root)的值
        binaryNode node  = new binaryNode(value);
        //把新节点的右子树设置为当前结点(root)的右子树
        node.right = right;
        //把新结点的左子树设置为当前结点(root)的左子树的右子树
        node.left = left.right;
        //把当前结点(root)的值换为左子节点的值
        value = left.value;
        //把当前结点(root)的左子树设置为左子树的左子树
        left = left.left;
        //（把当前结点（root）的右子树设置为新节点
        right = node;
    }
    
    //二叉排序树添加结点
    public void add(binaryNode node) {
        if(this == null) return ;
        if(node.value < this.value) { //如果添加结点的值比此结点的值小就往他的左边插
            if(this.left != null)
                this.left.add(node);
            else
                this.left = node;
        } else { //如果添加结点的值比此结点的值大，就往此节点的右子节点插
            if(this.right != null)
                this.right.add(node);
            else
                this.right = node;
        }
        //如果左子树高度和右子树高度不满足二叉平衡树，那么就进行旋转
        //左旋转
        if(rightHeight() - leftHeight() > 1) {
            if(right != null && right.leftHeight() > right.rightHeight())
                rightRotate();
            leftRotate();
            return ;
        }
        //右旋转
        if(leftHeight() - rightHeight() > 1) {
            if(left != null && left.rightHeight() > leftHeight())
                leftRotate();
            rightRotate();
        }
    }
}

右旋转的代码里面是完成了整个完整的左旋转和右旋转的代码，并且在左旋转和右旋转方法写完后，一定要在add（添加结点）函数里面写进去，就是在没插入一个结点的时候我们就要考虑是否需要进行平衡二叉树