[数据结构与算法]最小平方误差算法（LMSE） python实现

最小平方误差算法实验原理：

最小平方误差算法步骤：

（1）根据N个分属于两类的样本ω1，ω2 ，写成增广向量形式，将属于ω2的训练样本乘以（-1），写出规范化增广样本矩阵X。
（2）写出X的为逆矩阵：

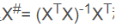
（3）设置初值c，设置初值b（1），c为正的校正增量，b(1)的各分量大于0，括号中次数代表迭代次数k=1。开始迭代：
计算：

…
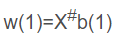
（4）计算，
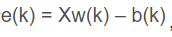进行可分性判别。
如果e(k)=0，模式线性可分，解为w(k)，算法结束。
如果e(k)>0，模式线性可分，有解，若进入第五步继续迭代，可使e(k)->0得到最优解。
如果e(k)<0，停止迭代解为w(k)，检查Xw(k)，若Xw(k)>0，有解；否则无解，模式线性不可分，算法结束。

（5）计算w(k+1) 和B(k+1)。
方法一:分别计算


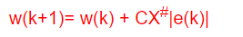
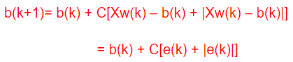
方法二：先计算：

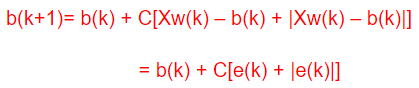
再计算：

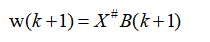
2.步骤：

①初始化数据
②编写程序入口函数if name == ‘main’:
③编写append_vector(data1, data2)函数，将数据规范化
④编写各种矩阵运算的矩阵，比如求逆函数INVERSE(A)；求转置函数transpose(matrix)，求矩阵相乘的函数MULTIPLY(A, B)；求矩阵相加和相减函数ADD(A, B)、SUBTRACT(A,B)；数乘以矩阵函数SCALA_MULTIPLY(A,num)。
⑤编写LMSE(X, X_inverse, x1, x2, W, B, c)函数，计算e(k)的值，进行线性判别。
⑥编写iteration(X, x1, x2, W, c, X_inverse, e, B)函数，调节B(k+1)和W(k+1),进行不断迭代，更新权值。
⑦编写randon_TestData(W)函数，产生测试数据集
⑧编写TestData(test, w)函数，对测试数据进行正确分类
⑨编写draw_scatter(x1, x2, w)函数，进行绘图

3.程序实现代码如下：

from numpy import *
import matplotlib.pyplot as plt

"""
maximum recursion depth exceeded in comparison 
报错提示超过最大递归深度。
修改递归深度,默认是1000次
该问题解决方式为加入如下脚本：
"""

import sys
sys.setrecursionlimit(100000)  # 例如这里设置为十万

x1 = [[0, 0], [0, 1]]
x2 = [[1, 0], [1, 1]]
# print("x1:", x1)
# print("x2:", x2)
B = [[1, 1, 1, 1]]
B1 = transpose(B)
# print("B1", B1)
c = 1


# 求增广向量
def append_vector(data1, data2):
    global ans
    global flag0
    new_data = []
    for i in data1:
        i.append(1)
        new_data.append(i)
    for j in data2:
        j.append(1)
        alist = []
        for k in j:
            alist.append(k * (-1))
        new_data.append(alist)
    # print("data:", new_data)
    return new_data


# 求伪逆矩阵
def inverse_matrix(data):
    T_data = transpose(data)
    tmp_data = MULTIPLY(T_data,data)
    # print("tmp_data:",tmp_data)
    inverse_data = INVERSE(tmp_data)
    # print("inverse_data:",inverse_data)
    result_data = MULTIPLY(inverse_data, T_data)
    # print("result_data", result_data)
    return result_data

def transpose(matrix):
    row, col = len(matrix), len(matrix[0])
    new_matrix = []
    for j in range(col):
        row_ = []
        for i in range(row):
            row_.append(matrix[i][j])

        new_matrix.append(row_)
    # print(new_matrix)
    return new_matrix

# 求代数余子式
def submatrix(A, i, j):
    # 矩阵A第i行第j列元素的余矩阵
    p = len(A)  # 矩阵的行数
    q = len(A[0])  # 矩阵的列数
    C = [[A[x][y] for y in range(q) if y != j] for x in range(p) if x != i]  # 列表解析
    return C

def det(A):
    # 按第一行展开递归求矩阵的行列式
    p = len(A)  # 矩阵的行数
    q = len(A[0])  # 矩阵的列数
    if(p == 1 and q == 1):
        return A[0][0]
    else:
        value = 0
        for j in range(q):
            value += ((-1)**(j+2))*A[0][j]*det(submatrix(A, 0, j))
        return value

# 求逆矩阵
def INVERSE(A):
    # print("A",A)
    p = len(A)#矩阵的行数
    q = len(A[0])#矩阵的列数
    # print("p,q:",p,q)
    C = [[0 for j in range(q)] for i in range(p)]
    # C=copy.deepcopy(A)
    # print("C:",C)
    d = det(A)
    # print(d)
    for i in range(p):
        for j in range(q):
            C[i][j] = ((-1)**(i+j+2))*det(submatrix(A, j, i))
            C[i][j] = C[i][j]/d
    # print(C)
    return C

def MULTIPLY(A, B):
    p = len(A)  # 矩阵A的行数
    q = len(A[0])  # 矩阵A的列数=矩阵B的行数
    r = len(B[0])  # 矩阵B的列数
    C = [[0 for j in range(r)] for i in range(p)]
    for i in range(p):
        for j in range(r):
            for k in range(q):
                C[i][j] += A[i][k]*B[k][j]
    # print(C)
    return C

def SUBTRACT(A,B):
    p = len(A)  # 矩阵的行数
    q = len(A[0])  # 矩阵的列数
    C= [[0 for j in range(q)] for i in range(p)]
    for i in range(p):
        for j in range(q):
            C[i][j] = A[i][j]-B[i][j]
    return C

def ADD(A, B):
    p = len(A)  # 矩阵的行数
    q = len(A[0])  # 矩阵的列数
    C = [[0 for j in range(q)] for i in range(p)]
    for i in range(p):
        for j in range(q):
            C[i][j] = A[i][j]+B[i][j]
    # print(C)
    return C

def SCALA_MULTIPLY(A,num):
    p = len(A)  # 矩阵的行数
    q = len(A[0])  # 矩阵的列数
    C = [[0 for j in range(q)] for i in range(p)]
    # C = copy.deepcopy(A)
    for i in range(p):
        for j in range(q):
            C[i][j] = A[i][j]*num
    # print(C)
    return C

def LMSE(X, X_inverse, x1, x2, W, B, c):
    print("第", ans, "次迭代")
    k = MULTIPLY(X, W)
    e = SUBTRACT(k, B)
    print("e:", e)
    flag = 0
    end = 0
    flag1 = 0
    for i in e:
        for j in i:
            if abs(j) < 1.0e-06:
                end = 1
            elif j >= 0:
                flag = 1
            else:
                flag1 = 1
    if end == 1 and flag == 0 and flag1 == 0:
        print("迭代结束，线性可分。")
        print("W:", W)
        draw_scatter(x1, x2, W)
        # plt.show()
        print("判别函数为：", "d(X) = ", W[0][0], " * x1 + ", W[1][0], " * x2 + ", W[2][0])
        if flag0 == 1:
            random_TestData(W)

    elif ans > 500 : # 迭代太多次没有收敛，强制结束
        print("迭代结束，线性不可分")

    elif end == 0 and flag == 0 and flag1 == 1:
        len_k = len(X)
        len_w = len(W[0])
        d = MULTIPLY(X,W)
        judge = 0
        for i in range(len_k):
            for j in range(len_w):
                if d[i][j] < 0:
                    judge = 1
                    break
            if judge == 1:
                break
        if judge == 0:
            iteration(X, x1, x2, W, c, X_inverse, e, B)
        else:
            print("迭代结束，线性不可分")

    else:
        iteration(X, x1, x2, W, c, X_inverse, e, B)


def iteration(X, x1, x2, W, c, X_inverse, e, B):
    global ans
    p = len(e)
    k = [[0 for j in range(1)] for i in range(p)]
    for i in range(len(k)):
        for j in range(len(k[0])):
            k[i][j] = abs(e[i][j])
    # print("k:",k)
    tmp_W = SCALA_MULTIPLY(X_inverse, c)
    t_W = MULTIPLY(tmp_W, k)
    W_k = ADD(W, t_W)
    t_e = ADD(e, k)
    t_B = SCALA_MULTIPLY(t_e, c)
    B_k = ADD(B, t_B)
    print("W_k", W_k)
    print("B_k",B_k)
    ans += 1
    LMSE(X, X_inverse, x1, x2, W_k, B_k, c)

def random_TestData(W):
    # 随机产生测试集
    test = []
    length = int(input("请输入产生随机数据集的待分类数据个数："))
    for j in range(length):
        generateddata = [random.randint(0, 100), random.randint(0, 100)]  # 二维
        if not generateddata in test:  # 去掉重复数据
            test.append(generateddata)
            TestData(generateddata, W)
        else:
            j += 1
    print("产生的随机测试数据为：", test)
    plt.show()

def TestData(test, w):
    # print("W", w)
    result = test[0]*w[0][0]+test[1]*w[1][0]+w[2][0]
    if result > 0:
        print(test, "属于第一类")
    else:
        print(test, "属于第二类")
    plt.scatter(test[0], test[1], c='b', marker='s')


def draw_scatter(x1, x2, w):
    plt.figure()
    n = len(x1)
    plt.title('Data-Analyse')
    plt.xlabel('x-value')
    plt.ylabel('y-value')
    for i in range(n):
        plt.scatter(x1[i][0], x1[i][1], c='r', marker='o')
        plt.scatter(x2[i][0], x2[i][1], c='g', marker='*')
    plt.grid()  # 显示网格线 1=True=默认显示
    if w[1][0] == 0:
        x = (-w[2][0])/w[0][0]
        plt.axvline(x=x)
    elif w[0][0] == 0:
        y = (-w[2][0])/w[1][0]
        plt.axhline(y=y)
    else:
        p1 = [-100, 100]
        p2 = [(-w[2][0] +100 * w[0][0]) / w[1][0], (-w[2][0] - 100 * w[0][0]) / w[1][0]]
        plt.plot(p1, p2)


if __name__ == '__main__':
    X = append_vector(x1, x2)
    ans = 0
    flag0 = 0
    X_inverse = inverse_matrix(X)  # 求伪逆矩阵
    W = MULTIPLY(X_inverse, B1)
    # print("W:",W)
    LMSE(X, X_inverse, x1, x2, W, B1, c)
    plt.show()
    # 产生随机数据集形成判别函数
    ans = 0
    flag0 = 1
    x1_points = []
    count = 0
    length = int(input("随机产生第一类数据，请输入第一类数据的长度（由于需要画图所以只产生二维数据）："))
    count += length
    for j in range(length):
        # generateddata = []
        generateddata = [random.randint(0, 100), random.randint(0, 100)]  # 二维
        if not generateddata in x1_points:  # 去掉重复数据
            x1_points.append(generateddata)
        else:
            j += 1
    print("产生的第一类随机数据为：", x1_points)

    x2_points = []
    length = int(input("随机产生第二类数据，请输入第二类数据的长度（由于需要画图所以只产生二维数据）："))
    count += length
    for j in range(length):
        # generateddata = []
        generateddata = [random.randint(0, 100), random.randint(0, 100)]  # 二维
        if not generateddata in x2_points:  # 去掉重复数据
            x2_points.append(generateddata)
        else:
            j += 1
    print("产生的第二类随机数据为：", x2_points)
    D = [[1 for i in range(count)]]  # 产生count行1列的全为1 的列表
    # print("D",D)
    D1 = transpose(D)
    print("D1",D1)
    data = append_vector(x1_points, x2_points)
    X_inverse = inverse_matrix(data)  # 求伪逆矩阵
    W = MULTIPLY(X_inverse, D1)
    # print("W:",W)
    nums = int(input("请输入调节C的次数："))
    for i in range(nums):
        c_test = eval(input("请输入c的值："))
        LMSE(data, X_inverse, x1_points, x2_points, W, D1, c_test)
        ans = 0

x1 = [[0, 0], [0, 1]]，x2 = [[1, 0], [1, 1]]，B = [[1, 1, 1, 1]]，c=1 # 初始权向量，这个数据的线性分类器结果如图1，图2所示。图2：e为误差，x2乘以-1，W的权值为W: [[-2.0], [0.0], [1.0]]，判别函数为：d(X) = -2.0 * x1 + 0.0 * x2 + 1.0。

图1：x1 = [[0, 0], [0, 1]]，x2 = [[1, 0], [1, 1]]LMSE判别的结果图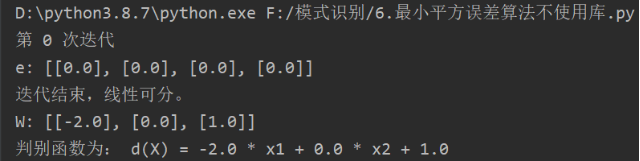图2：LMSE迭代结果随机产生两类数据x1_points，x2_points。X1_points=[[91, 18], [47, 71]]，x2_points= [[11, 90], [23, 90]]，设置c的调整次数为3次，第一次的c=1时：迭代54次之后线性可分，计算的权值为：W: [[0.1909119526253443], [0.13588885668027725], [-17.62097122869515]]，最后一次迭代的e=[[1.6651501866249419e-07],[-6.310042834911656e-07], [3.184234600439595e-07],[-7.829127213199172e-07]]。判别函数为：d(X) = 0.1909119526253443 * x1 + 0.13588885668027725 * x2 + -17.62097122869515。随机产生5个测试集：[[29, 46], [72, 2], [90, 25], [3, 87], [66, 22]]，测试分类结果。如图3所示

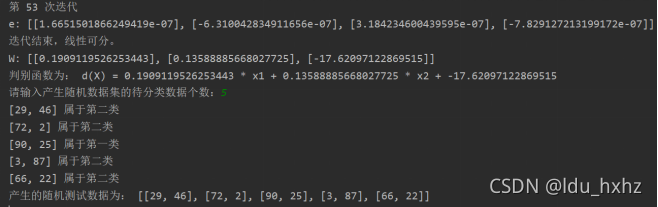
图3：c=1时 随机产生的数据集及随机测试集数据

图4五角星代表第二类数据，圆圈代表第一类数据，正方形代表测试数据的分类结果。

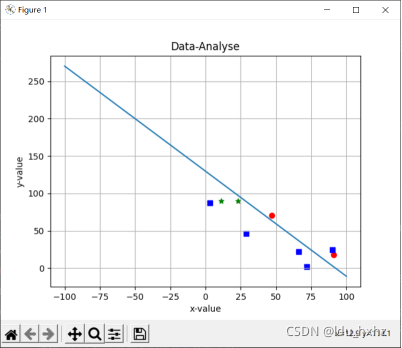
图4：c=1时 随机数据的LMSE判别结果以及随机测试集的分类结果

第二次调整c，c=2时：迭代24次之后线性可分，计算的权值为：W: [[0.1909119856753864], [0.1358888811742586], [-17.620974374822037]]。判别函数为： d(X) = 0.1909119856753864 * x1 + 0.1358888811742586 * x2 + -17.620974374822037
最后一次迭代的e: [[1.2790867032208553e-07], [-4.847065149249374e-07], [2.445972668851937e-07], [-6.013951256989003e-07]]。
随机产生10个测试集：[[36, 18], [13, 67], [1, 23], [91, 0], [33, 80], [25, 12], [21, 92], [96, 58], [22, 77], [87, 77]]，测试分类结果。如图5所示

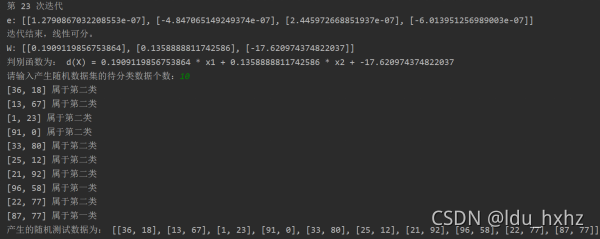
图5：c=2时 随机产生的数据集及随机测试集数据

图6圆圈代表第一类数据，五角星代表第二类数据，正方形代表测试数据的分类结果。

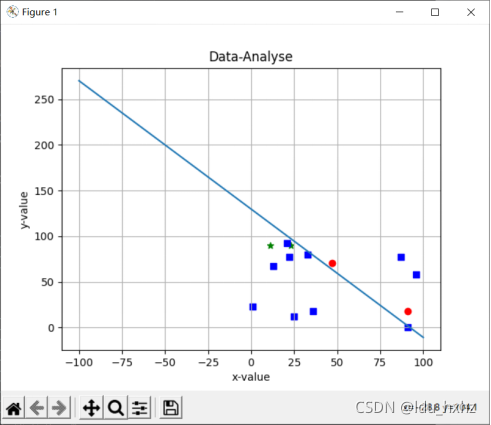
图6：c=2时 随机数据的LMSE判别结果以及随机测试集的分类结果

第三次调整c，c=3时：迭代13次之后线性可分，计算的权值为：W: [[0.19091195843548944], [0.1358888609858376], [-17.620971781757447]]判别函数为： d(X) = 0.19091195843548944 * x1 + 0.1358888609858376 * x2 + -17.620971781757447
最后一次迭代的e: [[1.5973666123159092e-07], [-6.052949714785427e-07], [3.054698876070461e-07], [-7.509841957187291e-07]]。
随机产生10个测试集：[[23, 36], [29, 59], [25, 29], [50, 45], [68, 5], [66, 80], [83, 86], [2, 53], [65, 68], [3, 88], [4, 62], [13, 39], [49, 69], [93, 16], [12, 58], [61, 67], [38, 39], [30, 61], [41, 97], [86, 83]]，测试分类结果。如图7、图8所示

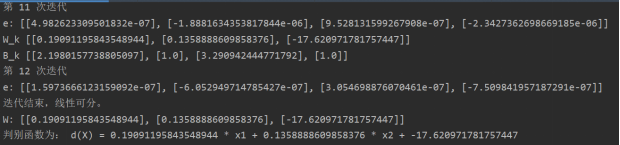
图7：c=3时 随机数据LMSE判别结果

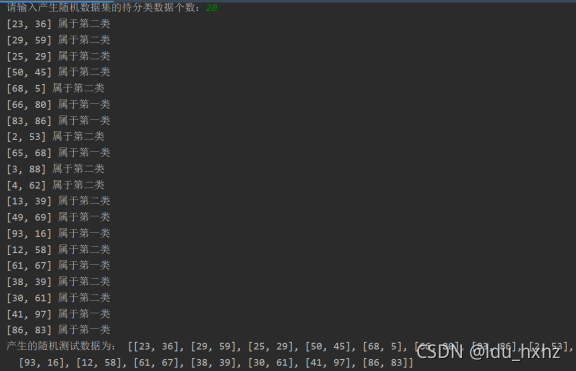
图8：c=3时 随机测试集数据分类结果
图9圆圈代表第一类数据，五角星代表第二类数据，正方形代表测试数据的分类结果。

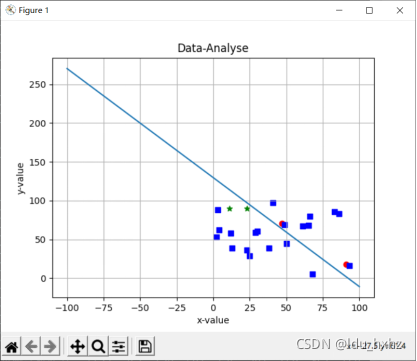
图9：c=3时 随机数据的LMSE判别结果以及随机测试集的分类结果

4.结果及分析：
实现了最小平方误差算法，可对多维数据进行线性判别，但由于最后为了画图，因此在产生随机数据的时候只产生二维数据，只是为了画图方便，多维数据不好画图展示。
实现了许多矩阵的运算，虽然可以直接调用numpy这个库中的方法来实现这些矩阵运算，简单且方便，但为了达到自我提升的要求，还是选择自己来实现这些运算，也是一种提高。写的第一个版本是调用numpy来实现的，这是经过改进的不调用numpy的版本。
最小平方误差算法不像感知器算法，感知器分类算法只对线性可分的数据有效，当数据线性不可分时，便会陷入死循环。但是最小平方误差算法对于线性不可分的数据会进行判别，不会陷入死循环的境地，它既适用于线性数据，也适用于非线性数据。
调整c的值，即学习效率，会影响感知器算法的收敛快慢，c的值不宜过大也不宜过小，c过大跳跃的过大，可能会出现略过满足结束条件的现象，难以收敛。c过小又收敛的太慢，因此需要找一个合适的c值。