剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
solution 1:动态规划
斐波那契数的边界条件是 F(0)=0 和 F(1)=1。当 n>1时,每一项的和都等于前两项的和,因此有如下递推关系:
F(n)=F(n-1)+F(n-2)
由于斐波那契数存在递推关系,因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系,边界条件为 F(0) 和 F(1)。
根据状态转移方程和边界条件,可以得到时间复杂度和空间复杂度都是 O(n) 的实现。由于 F(n)只和 F(n?1) 与 F(n-2)有关,因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)。如下的代码中给出的就是这种实现。

class Solution {
public:
int fib(int n) {
int MOD = 1000000007;
if (n < 2) {
return n;
}
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = (p + q)%MOD;
}
return r;
}
};
时间复杂度为O(n);
空间复杂度为O(1);
solution 2:矩阵快速幂
本题可以根据构造合适的矩阵乘法来实现 F(N) = F(N - 1) + F(N - 2) 中 F(N)、F(N - 1) 和 F(N - 2) 之间的依赖关系,利用 F(N - 1) 和 F(N - 2) 推导出 F(N) 。
根据矩阵乘法构造出
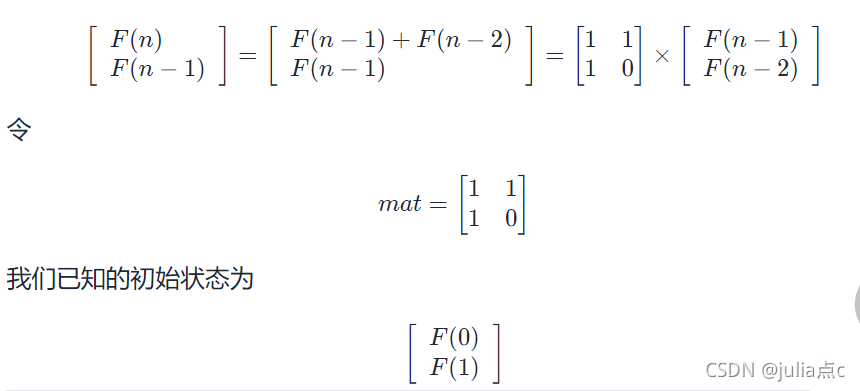

class Solution {
public:
const int MOD=1000000007;
int fib(int n) {
if (n <= 1)
return n;
vector<vector<long>> mat = {{1, 1},
{1, 0}};
vector<vector<long>> ans = {{1},
{0}};
int x = n - 1;
while (x != 0) {
if ((x & 1) != 0) ans = mul(mat, ans);
mat = mul(mat, mat);
x >>= 1;
}
return ans[0][0];
}
int mod = 1e9+7;
vector<vector<long>> mul(vector<vector<long>>& a, vector<vector<long>>& b){
int arow = a.size(); //a的行数
int brow = b.size(); //b的行数
int bcol = b[0].size(); //b的列数
vector<vector<long>> ans(arow,vector<long>(bcol,0)); //arow行bcol列,初始化为0
for(int i=0;i<arow;++i){
for(int j=0;j<bcol;++j){
for(int k=0;k<brow;++k){
ans[i][j] += a[i][k] * b[k][j];
ans[i][j] %= mod;
}
}
}
return ans;
}
};