K-Means聚类算法原理
给定样本集
D
=
{
x
1
,
x
2
,
…
,
x
m
}
D=\{\bm x_{1},\bm x_{2},\ldots,\bm x_m\}
D={x1?,x2?,…,xm?},K-Means算法针对聚类所得簇划分
C
=
{
C
1
,
C
2
,
…
,
C
k
}
C=\{C_1,C_2,\ldots,C_k\}
C={C1?,C2?,…,Ck?} 最小化平方误差
E
=
∑
i
=
1
k
∑
x
∈
C
i
∣
∣
x
?
μ
i
∣
∣
2
2
E=\sum_{i=1}^{k}\sum_{\bm{x}\in C_i}{||\bm{x}-\bm{\mu}_{i}||_2^2}
E=i=1∑k?x∈Ci?∑?∣∣x?μi?∣∣22?
其中
μ
i
=
1
∣
C
i
∣
∑
x
∈
C
i
x
\bm{\mu}_{i}=\frac{1}{|C_i|}\sum_{\bm{x}\in C_i}\bm{x}
μi?=∣Ci?∣1?∑x∈Ci??x 是簇
C
i
C_i
Ci? 的均值向量。直观来看,上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E 值越小则簇内样本相似度越高。
最小化平方误差是一个NP难问题,因此,K-Means算法采用了贪心策略,通过迭代优化来近似求解上式。算法流程如下图所示(注:该算法流程图出自周志华《机器学习》,清华大学出版社)。

数据集
air_data.csv数据集,其中包含62988条数据样本,均为某航空公司的客户乘机记录,包括会员号、入会时间、首次登机时间、性别等44个属性字段。
数据预处理
数据清洗
通过数据探索,发现数据中存在票价为空的记录和票价为0、平均折扣系数不为0、总飞行里程不为0的记录。由于原始数据量很大,缺失和异常数据所占比例较小,对于问题求解影响不大,因此对其进行丢弃处理。数据清洗后剩余62044条数据样本。
属性规约
原始数据中的属性有44个,针对航空公司客户价值分析的需要,根据LRFMC模型选择6个与客户价值分析密切相关的数据属性:FFP_DATE、LOAD_TIME、FLIGHT_COUNT、avg_discount、SEG_KM_SUM、LAST_TO_END。删除其他38个不相关、弱相关和冗余的数据属性。
数据变换
构造L、R、F、M、C这5个指标,主要采用数据变换的方式完成属性构造和数据标准化。L代表客户成为会员的时间,计算时用观测窗口的结束时间减去客户入会时间(以月为单位)。R代表客户最近一次乘坐航天公司飞机距观测窗口结束的时间(以月为单位)。F代表客户在观测窗口内乘坐航天公司飞机的次数。M代表客户在观测窗口内在航天公司累计的飞行里程(以千米为单位)。C代表客户在观测时间内乘坐舱位的平均折扣系数。
根据上述内容编写preprocess.py:
"""
Project Name : exp3
File Name : preprocess.py
Author : Chen Chunhan
Student ID : 04194041
Major & Class: Big Data 1902
Date : 2021-11-8 Mon.
"""
from datetime import datetime
import time
import numpy as np
import pandas as pd
def normal_date(date):
return datetime.strptime(date, '%Y/%m/%d')
def interval(date):
return date.days / 30
def preprocess(data):
data = data[data['SUM_YR_1'].notnull() & data['SUM_YR_2'].notnull()]
idx1 = data['SUM_YR_1'] != 0
idx2 = data['SUM_YR_2'] != 0
idx3 = (data['SEG_KM_SUM'] == 0) & (data['avg_discount'] == 0)
data = data[idx1 | idx2 | idx3]
data = data[['FFP_DATE', 'LOAD_TIME', 'FLIGHT_COUNT', 'avg_discount', 'SEG_KM_SUM', 'LAST_TO_END']]
new_data = pd.DataFrame()
new_data['L'] = (data['LOAD_TIME'].apply(normal_date) - data['FFP_DATE'].apply(normal_date)).apply(interval)
new_data['R'] = data['LAST_TO_END']
new_data['F'] = data['FLIGHT_COUNT']
new_data['M'] = data['SEG_KM_SUM']
new_data['C'] = data['avg_discount']
data_normal = (new_data - new_data.mean()) / new_data.std()
data_normal.columns = ['Z' + i for i in data_normal.columns]
return np.array(data_normal)
K-Means算法实现
根据算法流程编写my_k_means.py,其中包含my_k_means类,实现K-Means算法。
"""
Project Name : exp3
File Name : my_k_means.py
Author : Chen Chunhan
Student ID : 04194041
Major & Class: Big Data 1902
Date : 2021-11-8 Mon.
"""
import numpy as np
class my_k_means:
"""
基于NumPy实现k-means聚类算法
"""
def __init__(self, dataset, k, max_iters):
self.dataset = dataset
self.k = k
self.max_iters = max_iters
def init_centroids(self):
"""
k-means聚类算法初始化,随机选择k个点作为初始的聚类中心
:return: 随机选择的k个聚类中心
"""
centroids = self.dataset.copy()
np.random.shuffle(centroids)
return centroids[:self.k]
def closest_centroid(self, centroids):
"""
计算每个样本与聚类中心的欧氏距离,将其归入最近的簇
:param centroids: 聚类中心
:return: 聚类后样本所属的簇
"""
dist = np.sqrt(((self.dataset - centroids[:, np.newaxis]) ** 2).sum(axis=2))
return np.argmin(dist, axis=0)
def update_centroids(self, closest, centroids):
"""
对每个簇计算所有点的均值作为新的聚类中心
:param closest: 聚类后样本所属的簇
:param centroids: 上一轮迭代的聚类中心
:return: 新的聚类中心
"""
return np.array([self.dataset[closest == k].mean(axis=0) for k in range(centroids.shape[0])])
def k_means(self):
"""
k-means聚类算法实现
:return: 聚类后的簇划分
"""
centroids = self.init_centroids()
for i in range(self.max_iters):
closest = self.closest_centroid(centroids)
new_centroids = self.update_centroids(closest, centroids)
if (new_centroids == centroids).all():
break
centroids = new_centroids
return centroids, closest
对数据集进行聚类、可视化以及分析
编写main.py:
"""
Project Name : exp3
File Name : main.py
Author : Chen Chunhan
Student ID : 04194041
Major & Class: Big Data 1902
Date : 2021-11-8 Mon.
"""
import matplotlib.pyplot as plt
import pandas as pd
from my_k_means import my_k_means
from preprocess import preprocess
data = pd.read_csv('./air_data.csv', encoding='utf-8')
# 数据清洗
data = preprocess(data)
# print(data)
# k-means聚类
model = my_k_means(dataset=data, k=5, max_iters=10000)
res = model.k_means()
print(res[0])
# 聚类结果可视化
X = ['ZL', 'ZR', 'ZF', 'ZM', 'ZC']
style = ['-', '--', ':', '-.', ':']
for i in range(5):
if i == 4:
plt.plot(X, res[0][i], label='cluster' + str(i), linewidth=5, linestyle=style[i], marker='*')
else:
plt.plot(X, res[0][i], label='cluster' + str(i), linewidth=2, linestyle=style[i], marker='o')
plt.xlabel('LRFMC')
plt.ylabel('Values')
plt.title('Result of k-means clustering')
plt.legend()
plt.savefig('./result.png')
plt.show()
运行结果如下图所示:
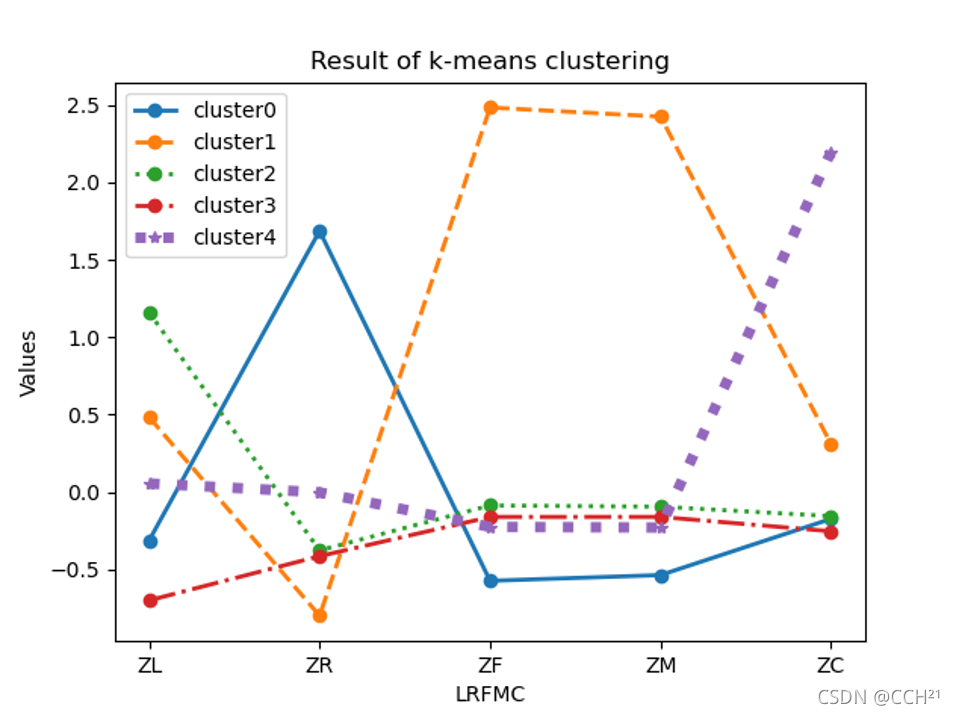
通过K-Means聚类算法,客户数据样本被划分为了5个客户群。各客户群的中心点如下:
- 客户群1为
[-0.313474526, 1.68619945, -0.573966983, -0.536785938, -0.173345207]。 - 客户群2为
[0.482914246, -0.799395648, 2.48336098, 2.42457094, 0.308554298]。 - 客户群3为
[1.16029338, -0.377277679, -0.0871028637, -0.0949810559, -0.155938247]。 - 客户群4为
[-0.700374491, -0.414712961, -0.161308550, -0.161159503, -0.253786224]。 - 客户群5为
[0.0548431078, -0.002.41696765, -0.225711273, -0.229724402, 2.19808384]。
根据航空公司的业务定义为5个等级的客户类别:
- 重要保持客户:平均折扣率高,乘坐次数或里程高,最近坐过本公司航班。
- 重要发展客户:平均折扣率较高,乘坐次数和里程较低。
- 重要挽留客户:平均折扣率、乘坐次数或者里程较高,较长时间没坐本公司航班。
- 一般客户与低价值客户:折扣率低,较长时间未坐本公司航班,乘坐次数或里程较低,入会时长短。
根据每种客户群类型的特征对客户群进行客户价值排名,以便获得高价值客户的信息。
- 客户群1是一般客户群。
- 客户群2的F、M很高,L也不低,是重点保持的客户群。
- 客户群3是重点挽留客户群,他们入会时间长,但是F、M较低。
- 客户群4是低价值客户群。
- 客户群5是重点发展客户群。
参考文献
[1] 孙家泽, 王曙燕. 数据挖掘算法与应用(Python实现)[M]. 北京: 清华大学出版社, 2020: 353-362.
[2] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 202-204.