前言

不小心看到这篇文章的哥哥姐姐们，你们就当这是个刷题链接的帖子。

今天的题目对于我这种five来说太难了，做出来的题目都模棱两可（滑稽）。

原文链接：《算法零基础100讲》(第30讲) 概率与统计

1227. 飞机座位分配概率

原题链接：1227. 飞机座位分配概率

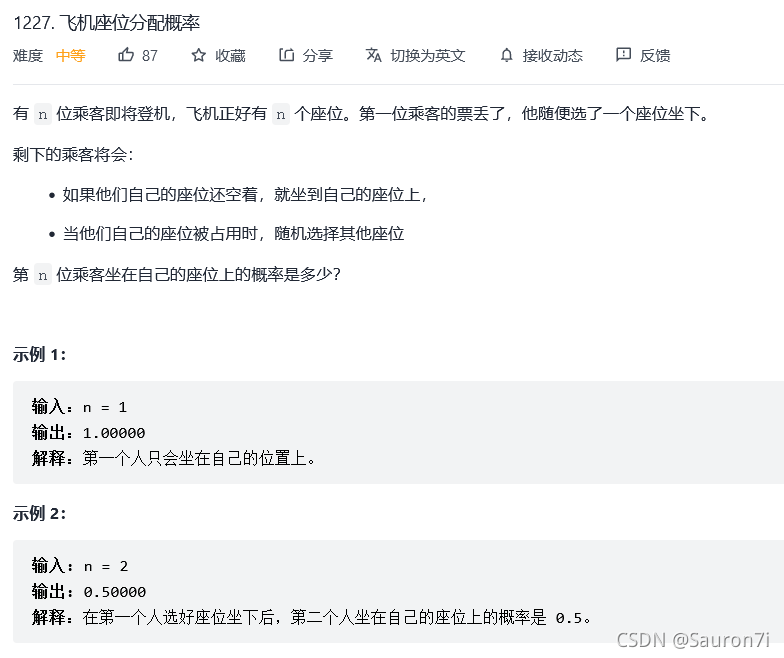
在这里插入图片描述

分析

恍然大悟：
只要第一个人没坐我的位置，那么没票的人就变成了第二个人，以此类推，只有一个没票的人跟我抢座位，那就是1/2。

代码

class Solution {
public:
    double nthPersonGetsNthSeat(int n)
    {
        return n == 1 ? 1 : 0.5;
    }
};

LCP 11. 期望个数统计

原题链接：LCP 11. 期望个数统计

在这里插入图片描述

代码

其实就是统计能力值的个数
这里用到C++里的 set

class Solution {
public:
    int expectNumber(vector<int>& scores)
    {
        set<int> s(scores.begin(), scores.end());
        return s.size();
    }
};

470. 用 Rand7() 实现 Rand10()

原题链接：470. 用 Rand7() 实现 Rand10()

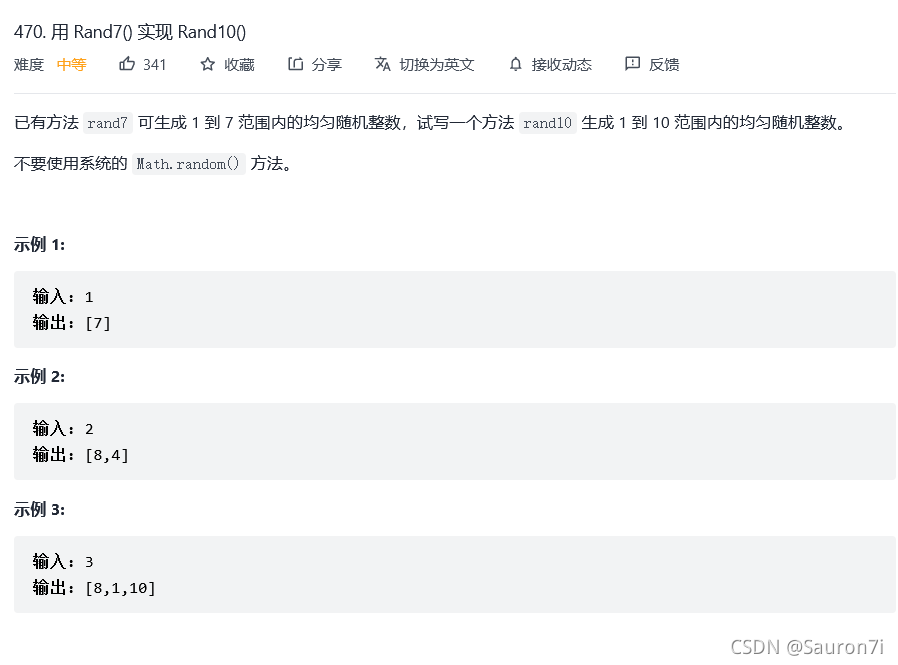
在这里插入图片描述

法1

既然是要求 rand10()，那可以利用 1/2 * 1/5可以得到 1/10的概率

代码：

class Solution {
public:
    int rand10()
    {
        int a = rand7(), b = rand7();

        while (a == 7)
        {
            a = rand7();
        }
        while (b > 5)
        {
            b = rand7();
        }

        return (a & 1 ? 0 : 5) + b;
    }
};

法2——偷鸡法

因为rand7()生成随机【1~7】，那使用十个rand7()，再对10取模加一，达到 rand10()的效果。

其实这样的概率是错误的，生成的随机数再累加，中间部分的数字概率会比两边大，形成一种正态分布，但提交能通过。。。

代码

class Solution {
public:
    int rand10()
    {
        int tmp = 0, i = 0;

        while (i++ < 10)
        {
            tmp += rand7();
        }

        return (tmp % 10 + 1);
    }
};