回归分析只涉及到两个变量的,称一元回归分析。一元回归的主要任务是从两个相关变量中的一个变量去估计另一个变量,被估计的变量,称因变量,可设为Y;估计出的变量,称自变量,设为X。回归分析就是要找出一个数学模型Y=f(X),使得从X估计Y可以用一个函数式去计算。当Y=f(X)的形式是一个直线方程时,称为一元线性回归
一元一元线性回归的主要利用两种方法
1? ?最小二乘法
2? 梯度下降法
我主要开始学习梯度下降法
梯度下降法:
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。
对于一元函数来说梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向,通俗来说也就是导数的方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。主要目的就是通过不断的迭代来达到求出最小值所对应的横坐标的过程。
Xnew=Xold-a *f'(Xold)
a 为学习效率(也可以理解为下山的步伐)
b为每次迭代X的变化量? b=Xold-Xnew。
a可以自己设定不易过大或过小,过大容易造成不准确,过小容易造成迭代次数过多。
下面来看看例子
y=(x-2.5)2+3
f'(x)=2x-5;
我们一般通过两种方式控制迭代次数?
1:是b的大小就是X的变换量? ?
2:给定迭代执行的次数

下面看看代码运行
 ?
?
 ?
?
 ?
?
?现在我们用梯度下降法求一元线性回归函数
首先设出线性回归方程
hθ?(x)=θ0?x+θ1
其中我们要确定的是θ0?与θ1;
我们想要的函数一定是要与给定样本数值的误差越小越好,现在我们引入损失函数。
J(θ0?,θ1?)=2m1?i=1∑m?(hθ?(xi)?yi)2
分别对θ0? 和??θ1求导
?θ0??J(θ0?,θ1?)?=m1?i=1∑m?(θ0?+θ1?xi?yi)
?θ1??J(θ0?,θ1?)?=m1?i=1∑m?(θ0?+θ1?xi?yi)xi
θ:=θ?η?m1?i=1∑m??θ?J(θ,xi,yi)?
分别采用梯度下降法求出最合适的θ0? 与??θ1? 就是使找出能够使J(θ0?,θ1?)=2m1?i=1∑m?(hθ?(xi)?yi)2函数可以取得尽可能小的值。
下面我们看一个例子
通过分析披萨的直径与价格的线性关系,来预测任一直径的披萨的价格。
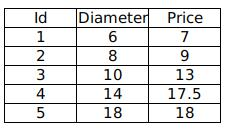
?其中 Diameter 为披萨直径,单位为“英寸”; Price 为披萨价格,单位为“美元”。
用一元线性回归方法求出其回归方程。
可以用python实现

 ?
?
 ?
?
?
?
?