[数据结构与算法]池塘抽水 c++ dfs详解

题目描述

题目描述

??你刚刚承包了一块大小为 M * N （1<=M, N<=1000）的地块，现要利用这片区域开发成商业用地，但之前该地块是一个渔场所在地，因此分布着许多大小不一的池塘，现在需要把所有的这些池塘里的水抽干并填平。 现在你想知道至少需要多少台抽水机器才能将这片区域的所有池塘抽干。如果池塘的区域互相连接，那么这些区域可以使用同一台机器。例如：若 M = 1, N = 5，其中(1, 1), (1, 2)和(1, 4)区域有池塘，那么由于(1, 1)和(1, 2)这两块区域连在一起,所以只需要两台机器即可采完所有池塘。（注意，池塘如果上、下、左、右相邻以及对角线相邻都属于相连的情况）

输入格式

??输入的数据有多组，每组数据首先是两个正整数 M 和 N，表示地块的尺寸，接下来是一个 M 行N 列的矩阵，矩阵中有两种可能的值，一种是“*”，表示此处没有池塘，一种是“@”，代表此处为池塘。若 M, N 均为 0，则表示输入结束，该组数据无需输出任何结果。

输出格式

???对于每组数据，在一行内输出需要的抽水机器数量。

输入样例

1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

输出样例

0
1
2
2

解题思路

题意

??简单的说，题目是求独立的池塘的个数。把地块按下标分成 M * N 的方格，每个池塘方格与上、下、左、右相邻以及对角线相邻的池塘方格相连。输入中 * 表示没有池塘的方格， @ 表示有池塘的方格。当输入（0,0）时，结束输出。

思路

??遍历所有的地块方格，每找到一个池塘方格，放置抽水机将这一整片池塘抽干（把 @ 变成 * 或者其他字符），重复操作直到遍历结束，得到总共抽干池塘的次数也就是需要的抽水机数量。

??使用深度优先搜索思想，先定位到一个池塘方格，把当前方格抽干并依次往相邻的八个方向移动，继续抽干当前的池塘方格和向周围搜索的操作，直到移动到地图边界或者非池塘的方格，不做任何操作并返回上一个方格，继续向其它方向搜索。最终回到初始位置完成递归搜索。因为递归过程是将当前的池塘方格抽干并移动至周围的方格，当前方格的状态不影响移动操作，所以不需要额外的回溯操作。

样例图解

5    5
*  *  *  *  @
*  @  @  *  @
*  @  *  *  @
@  @  @  *  @
@  @  *  *  @

用蓝色方格代表池塘方格，绿色方格代表非池塘方格。

地块原状态

从（1,1）位置从左往右、从上往下遍历，找到第一个位置（1,5），放入第一台抽水机

进行递归抽水的操作，首先将当前位置池塘方格抽干

然后判断，左下、左、左上、上、右上、右、右下均不合要求，移动到下面一格

重复抽水和移动操作至填满当前池塘

无可抽水位置，按移动位置依次回退，每回退一个位置继续判断是否可以抽水

回到初始位置（1,5），判断结束后退出抽水操作并开始搜索下一个池塘方格位置，放置第二台抽水机（2,2）

继续抽水并以左下，左，左上，上，右上，右，右下，下的顺序移动搜索

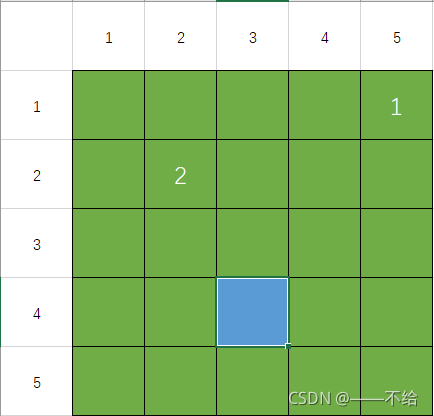
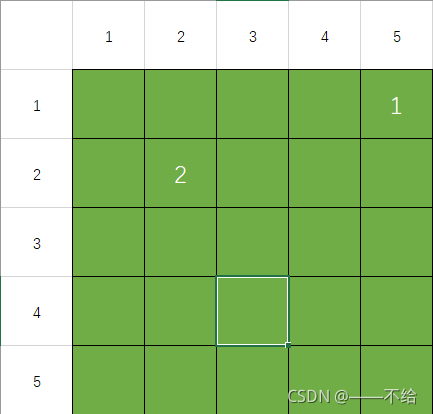
依次回退上一位置并继续判断，直到回到第二台抽水机位置（2,2），完成抽水操作。

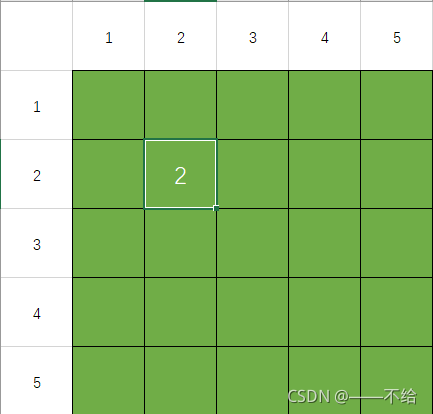
继续搜索放置饮水机的位置，遍历完地块后算法结束

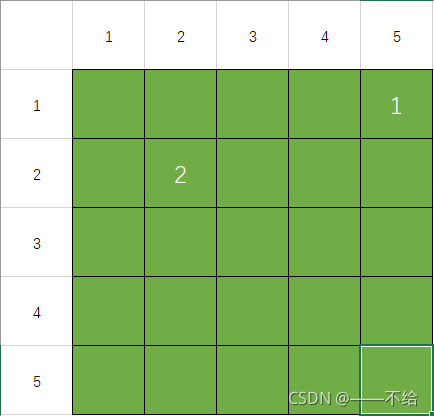
总共抽水机台数为2台

解题代码

定义变量

定义地块方格数组 block 和地块尺寸变量 M、N，记录抽水机数量的变量 cnt

const int SIZE = 1007;
int cnt = 0;
int M, N;
char block[SIZE][SIZE];

定义实现左下、左、左上、上、右上、右、右下、下移动的数组

int x[8] = { 1, 0, -1, -1, -1, 0, 1, 1 };
int y[8] = { -1, -1, -1, 0, 1, 1, 1, 0 };

通过原坐标（px, py）加上（x[i], y[i]）实现坐标的移动（px + x[i], py + y[i]），例

int px = 2, py = 2;
for (int i = 0; i < 8; i++)
{
    //依次添加坐标，向指定方向移动
	px += x[i];
	py += y[i];
    cout << "(" << px << "," << py << ")" << endl;
    //回到移动前位置，减去添加的坐标
    px -= x[i];
    py -= y[i];
}

/*
输出结果
(3,1)
(2,1)
(1,1)
(1,2)
(1,3)
(2,3)
(3,3)
(3,2)
*/

读入数据

读入多组数据，读到（0,0）结束

while (cin >> M >> N)
{
    if (M == 0 && N == 0)
    {
        break;
    }
}

读入地块

void readBlock()
{
	for (int i = 1; i <= M; i++)
	{
		for (int j = 1; j <= N; j++)
		{
//scanf("%c", &block[i][j]) 和 block[i][j] = getchar() 需要处理输入时换行时的 '\n'
//例如在换行后的读入前加 getchar()
			cin >> block[i][j];
		}
	}
}

算法实现

初始化 cnt 变量，遍历地块，寻找到池塘方格时放置抽水机并开始抽水

void solve()
{
	cnt = 0;
	for (int i = 1; i <= M; i++)
	{
		for (int j = 1; j <= N; j++)
		{
			if (block[i][j] == '@')
			{
				//放置抽水机，数量+1
				cnt++;
                 //以当前位置开始进入函数进行深搜抽水
				dfs(i, j);
			}
		}
	}
}

深搜实现

void dfs(int px, int py)
{
    //判断是否超过地块范围，超过则停止操作回到上一位置
	if (px < 1 || px > M || py < 1 || py > N)
		return;
	//判断当前位置，不是池塘方格则停止操作，回到上一位置
	if (block[px][py] != '@')
		return;
	
    //抽掉当前位置的水
	block[px][py] = '*';

    //遍历八个方向，依次移动
	for (int i = 0; i < 8; i++)
	{
        //添加相应坐标移动位置
		px += x[i], py += y[i];
        //以移动后的位置进入深搜程序，执行抽水和移动操作
		dfs(px, py);
     	//当前位置（px, py）深搜完后，减去添加的坐标返回移动之前的位置，继续其它位置进行深搜
		px -= x[i], py -= y[i];
	}
}

输出结果

直接输出抽水机数量 cnt

cout << cnt << endl;

整体代码

#include <iostream>

using namespace std;

const int SIZE = 1007;
int cnt = 0;
int M, N;
char block[SIZE][SIZE];

int x[8] = { 1, 0, -1, -1, -1, 0, 1, 1 };
int y[8] = { -1, -1, -1, 0, 1, 1, 1, 0 };

void readBlock()
{
	for (int i = 1; i <= M; i++)
	{
		for (int j = 1; j <= N; j++)
		{
			cin >> block[i][j];
		}
	}
}

void dfs(int px, int py)
{
	if (px < 1 || px > M || py < 1 || py > N)
		return;

	if (block[px][py] != '@')
		return;

	block[px][py] = '*';

	for (int i = 0; i < 8; i++)
	{
		px += x[i], py += y[i];
		dfs(px, py);
		px -= x[i], py -= y[i];
	}
}

void solve()
{
	cnt = 0;
	for (int i = 1; i <= M; i++)
	{
		for (int j = 1; j <= N; j++)
		{
			if (block[i][j] == '@')
			{
				cnt++;
				dfs(i, j);
			}
		}
	}
	cout << cnt << endl;
}

int main()
{
	while (cin >> M >> N)
	{
		if (M == 0 && N == 0)
		{
			break;
		}
		readBlock();
		solve();
	}

	return 0;
}

运行结果