1.前言
对初学递归的人来说,递归无疑是很不好理解的,本系列旨在对常见算法中使用的递归做一定程度的解析,学习这些算法的同时,总结出其递归模型。以便于加深对递归的理解,同时,当我们掌握了多种递归模型。那无论何时需要使用递归解决问题,我们都能从已有的递归模型中得到一些启发。或者相似的场景使用的模型是一样时(类似于数学或物理中的建模,通过对具有某类特征的事物的分析,总结出其一般规律,以便应用到具有相同特征的情况中去),我们便能套用已有的模型使用,相信会很方便。
2.归并排序
1.算法理解
摘自百度百科
归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
简单来说就是将一个序列分成两个序列,将两个序列排好序后再按大小顺序合并回去,在归并排序里我们会将一个序列递归的分割,直至其某一个子序列被分成两个只含一个元素的子序列。因为其只含一个元素,所以我们可以认为他有序,也就不用排序了。递归结束,开始回升合并。
举个例子便于理解归并排序:
有如下数据需要排序:
{1,4,2,65,76,15,9,0,54,32};
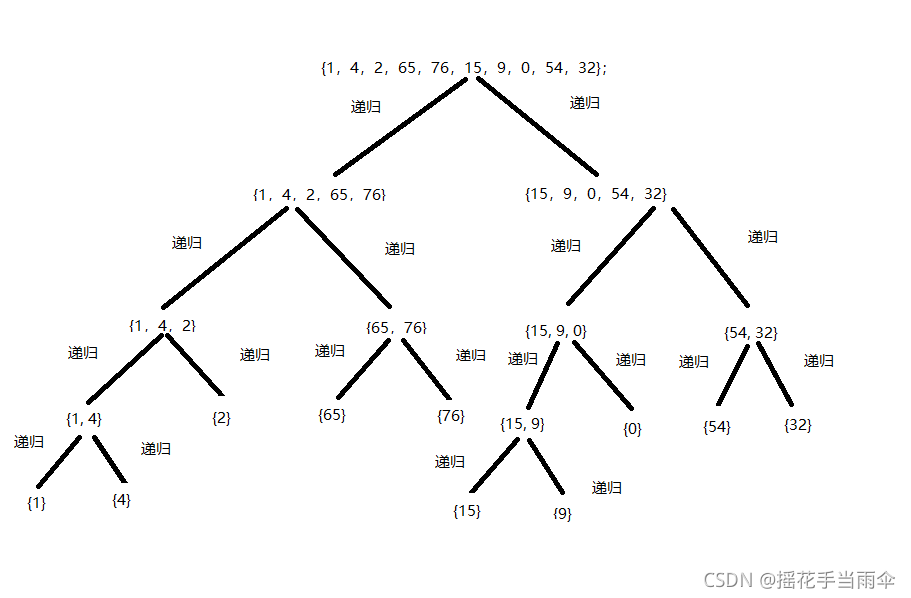
我们首先使用递归深度的将上述数据分割成不可分割的子序列,即每个序列只有一个数据。分割过程为:
先分割{1,4,2,65,76,15,9,0,54,32},被分割为:
{1,4,2,65,76} {15,9,0,54,32};
{1,4,2,65,76} 继续递归分割为{1,4,2}与{65,76};
{1,4,2}继续分割为{1,4}与{2};
{1,4}继续分割为{1}与{4};
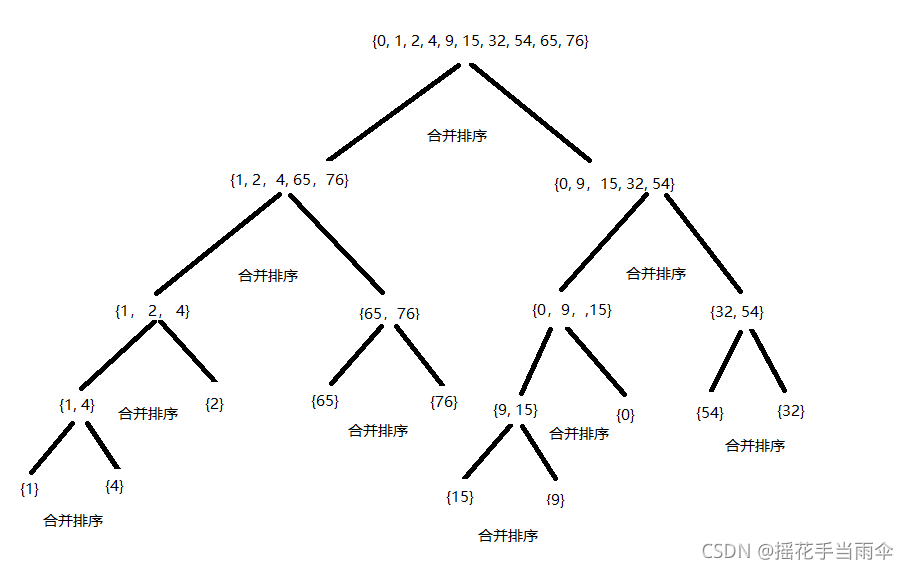
至此{1,4}序列变为了最小的不可再分的序列,递归开始回升返回,开始合并{1},{4}为一个有序序列。合并后为{1,4}该函数返回,处理与{1,4}一起分割出来的另一个序列{2},{2}为最小序列不用再分割返回与{1,4}合并成一个有序序列,为{1,2,4},该层函数返回,递归处理与{1,4,2}一起分割出来的{65,76} ,则{65,76}被分割为{65}与{76},递归回升合并{65},{76},返回后为{65,76},然后{65,76}与{1,2,4}合并为一个有序序列{1,2,4,65,76},函数返回处理 {15,9,0,54,32},直至{15,9,0,54,32}被处理为{0,9,15,32,54}返回与{1,2,4,65,76}合并为{0,1,2,4,9,15,32,54,65,76}。自此函数结束。
可能这样说还是不直观,看几张图以便理解:
接下来只剩一个点了,那就是合并有序序列的方法,其实这一步很简单:
举个例子:合并有序序列{1,2,4}与{65,76} 。首先从两个序列中各取出一个数分别为1与65,比较,1小,1先存入新的序列得{1} 。再从第一个序列取数为2,比较2小存入序列得{1,2} 。取4,比较,存入序列得{1,2,4} 。
此时第一个序列已经没有数据了。又因为序列都是有序的。所以只需第二个序列的数依次存入新序列就行了。
图1为递归调用的过程,图2为递归回升合并排序的过程。
2.代码
#include <iostream>
#include <Windows.h>
#include <stdio.h>
#include <string.h>
using namespace std;
int Sort(int* nums,int left,int mid,int right,int* tmp) { //合并函数,创建一个临时数组,比较两个数组的元素大小,小的进入临时数组,直至两数组都为空
int left_tmp = left;
int mid_tmp = mid + 1;
int count = 0;
while (left_tmp <= mid && mid_tmp <= right) { //将其中一个数组的元素全部存入临时数组
if (nums[left_tmp] < nums[mid_tmp]) {
tmp[count++] = nums[left_tmp++];
}
else {
tmp[count++] = nums[mid_tmp++];
}
}
while (left_tmp <= mid) { //再把另一个不为空的数组的元素全部存入数组中
tmp[count++] = nums[left_tmp++];
}
while (mid_tmp <= right) { //再把另一个不为空的数组的元素全部存入数组中
tmp[count++] = nums[mid_tmp++];
}
memcpy(nums + left, tmp, sizeof(int) * (right - left + 1)); //将临时数组中的元素全部存入nums数组
return 1;
}
int mergeSort(int* nums, int left, int right, int* tmp) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid, tmp); //递归拆分数组,直至数组中只有一个元素
mergeSort(nums, mid + 1, right, tmp);
Sort(nums, left, mid, right, tmp); //合并数组
}
return 1;
}
int main(void) {
int nums[10] = { 1,4,2,65,76,15,9,0,54,32 };
//int nums[10] = { 1,4,2,6,7,15,9,0,5,33 };
//int nums[10] = { 1,2,3,4,5,6,7,8,9,10 };
int count = sizeof(nums) / sizeof(nums[0]); //计算临时数组大小
int* tmp = new int[count]; //分配临时数组空间
mergeSort(nums, 0, 9, tmp);
for (auto& art : nums) { //打印nums元素
cout << art << " ";
}
system("pause");
return 0;
}
3.递归模型总结
mergeSort(nums, left, mid, tmp);
mergeSort(nums, mid + 1, right, tmp);
Sort(nums, left, mid, right, tmp);
对递归的理解需要一些抽象思维,如果只在当前角度来看,不深入到递归的最底层。mergeSort(nums, left, mid, tmp)函数就可以看成一个排序函数,它会把nums数组从left到mid的元素从小到大排好序,mergeSort(nums, mid + 1, right, tmp)函数也一样将nums数组中从mid+1到right的数据排好序。两个函数都完成后,执行Sort(nums, left, mid, right, tmp),即把两个已经有序的数组从小到大合并排序。实际上递归的每一层都是这样实现的。
归并排序其实是分治法的一个非常典型的应用,分治法算是递归的一类模型,它的特征是通过把原问题一分为二,直至其被分为我们想要的最小子问题(代码体现为:mergeSort(nums, left, mid, tmp) 与 mergeSort(nums, mid + 1, right, tmp))。在归并排序中即原数组被分为只含一个元素的数组。然后递归回升,开始对分开的子序列进行我们想要的处理(代码体现为:Sort(nums, left, mid, right, tmp) )。
其递归模型为先递归,直至两个递归回升,再对其进行处理。
再抽象一点结合代码理解就是由于分治法是一分为二,两路进行,所以递归函数里有两次递归,由于递归后往往要进行某些处理,所以还有进行处理的一步。还有一点值得注意的是:进行处理的一步未必是写在递归之后。还有可能是这样的:
mergeSort(nums, left, mid, tmp);
Sort(nums, left, mid, right, tmp);
mergeSort(nums, mid + 1, right, tmp);
还可能是这样的:
Sort(nums, left, mid, right, tmp);
mergeSort(nums, left, mid, tmp);
mergeSort(nums, mid + 1, right, tmp);
4.企业实战
1.问题:如果有一个100G的文件需要排序,但内存最大只能容纳1G的文件,那么怎么才能把文件里的数据排好序呢?
2.解决方法:我们可以使用类似归并排序的方法把100G的文件分成两个50G的文件,把50G的文件分成两个25G的文件,再继续细分下去,直至其被分成可在内存里操作的大小,将其在内存里排好序后写回文件中。比如我们最终把一个2G的文件细分为两个1G的文件,两个1G的文件在内存中排好序后写回到文件中,得到了两个排好序的1G文件,再使用我们在归并排序中使用的排序方法就能1G的内存中排好两个1G的文件得到一个2G的文件(实际上此时排序10MB的内存都够了,因为我每次只需要取出两个数比较大小再存入文件就行了。每次只需要两个数的空间)。以此类推,再大的文件都可以排好序。