前提引入
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:xx 和 yy 是亲戚,yy 和 zz 是亲戚,那么 xx 和 zz 也是亲戚。如果 xx,yy 是亲戚,那么 xx 的亲戚都是 yy 的亲戚,yy 的亲戚也都是 xx 的亲戚。
输入格式
第一行:三个整数n,m,p,(n<=5000,m<=5000,p<=5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Mi和Mj具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
输出格式
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
输入输出样例
输入
6 5 3 1 2 1 5 3 4 5 2 1 3 1 4 2 3 5 6
输出
Yes Yes No
看到这道题会有什么想法呢?
因为最近在学数据结构,很自然的想到了利用图来解决,构建一个图,每个人即一个顶点,存在亲属关系即顶点与顶点之间存在边。本题即可转化为,查找图的连通集,查看元素是否在连通集内。如果不考虑运行时间的话这么做是完全没有问题的,只是代码略微麻烦。经过一番查找后,发现大家都在用并查集去做,便学习了一下 这个算法!
算法介绍
“并查集”:在一些有N个元素的集合应用问题中,通常是在初始时让每个元素构成一个单元素的集合,然后按一定顺序(或者叫传递)将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
“并”:也就是合并,把两个不相交的集合合并为一个集合。
“查”:也就是查询,查询两个元素是否在同一个集合中。
并查集的重要思想在于,用集合中的一个元素代表集合。(代表元素,也就是标志,就像队伍中的队头)。我曾看过一个有趣的比喻,把集合比喻成帮派,而代表元素则是帮主。接下来我们利用这个比喻,看看并查集是如何运作的。
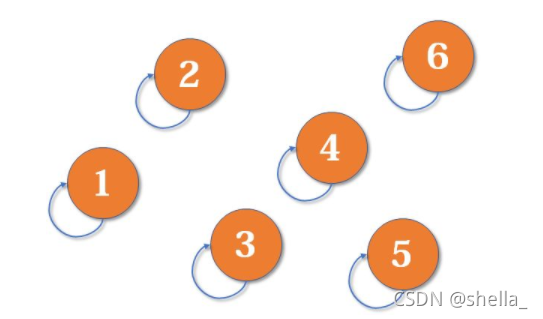
江湖的最初的局面,武艺高超的各位大侠自成一派。他们各自的帮主自然就是自己,图中每个元素的箭头指向他的帮主。(对于只有一个元素的集合,代表元素自然是唯一的那个元素。)
现在江湖大战,胜者为王,败者为寇。
首先1号和3号比武,假如1号赢了,那么3号就认1号作帮主,江湖局面变成下图(合并1号和3号所在的集合,1号为代表元素)。
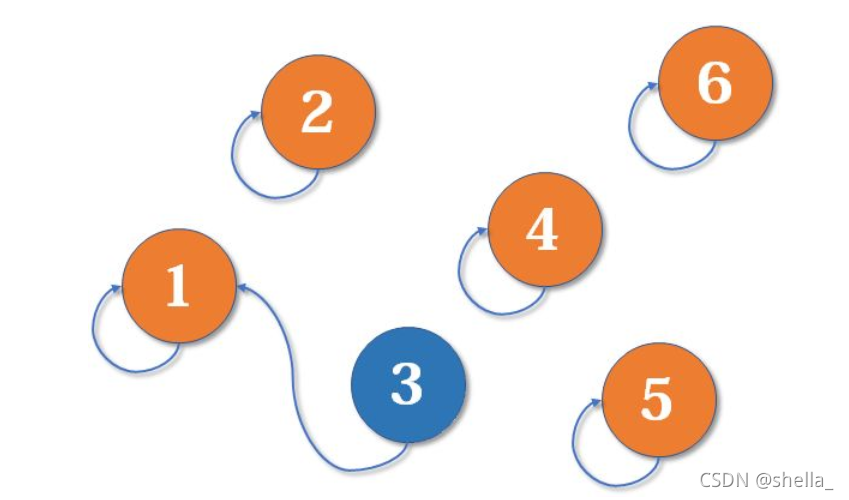
现在2号想和3号比武(合并3号和2号所在的集合),但3号表示,别跟我打,打赢我没用,打赢我大哥我才服你。这次又是1号赢了,那么2号也认1号做帮主(合并代表元素)。
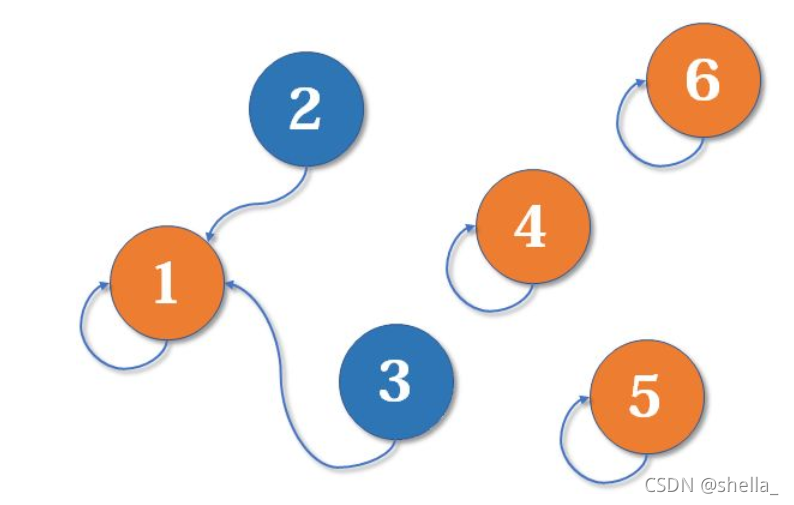
现在在我们假设4、5、6号也进行了一番帮派合并,江湖局势变成下面这样:
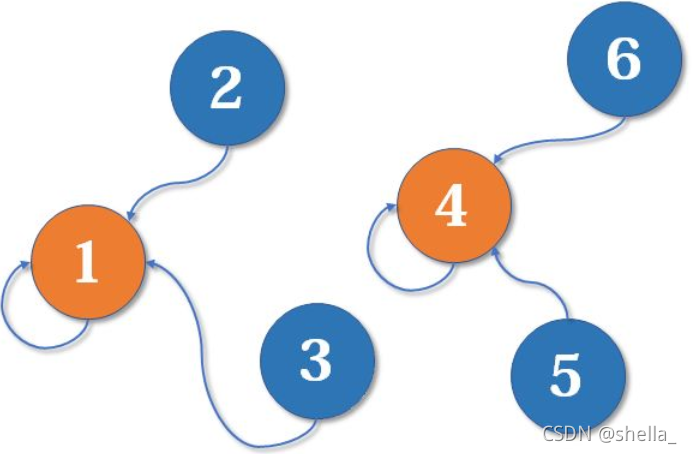
现在是两个初具规模的门派,为争夺武林第一门派。两大帮派进行了宣战,两大帮主出战最后还是1号带领帮派成为第一门派,而4号带着他帮派的小弟,归附了第一门派。
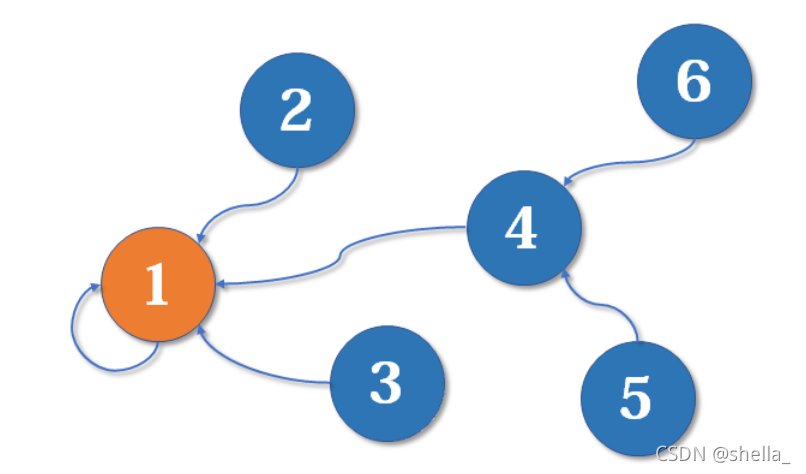
对于并查集算法,最重要的即使“并”和“查”。通过刚才的帮派比拼,我们已经完成了“并”的操作,那么我们如何“查”他们是否是同一个帮派呢?江湖上两个小弟相遇,刚欲打斗,忽然问到:你老大是谁?小弟5号说:我老大是1号! 小弟2号说:我老大也是1号!原来我们是一家人,不打了不打了,两人结伴回帮派了。
5号自报家门时,提的并不是他的直接老大4号,而是终极BOSS1号。如果他提的是4号,2号会表示谁啊谁啊不认识。这就是我们为什么要设置代表元素的原因!
好啦,回归现实世界。我们仔细看看江湖局面,是不是像一棵树。
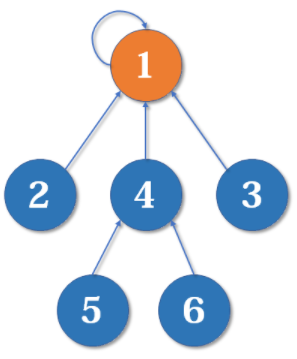
要寻找集合的代表元素,只需要一层一层往上访问父节点(图中箭头所指的圆),直达树的根节点(图中橙色的圆)即可。根节点的父节点是它自己。
代码实现
基础的核心代码分为三部分:
- 初始化集合
- 查询其代表元素
- 合并两集合
初始化
fa [ ] :数组用来存储元素的父结点(升级版存储代表元素)
fa [ 2 ] = 1;----------------------表示2号的父节点为1号
int fa[MAXN];
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
fa[i] = i;
}
初始时,每个元素的父节点都是它本身。
查询
int find(int x)
{
if(fa[x] == x)
return x;
else
return find(fa[x]);
}
我们用递归的写法实现对代表元素的查询:如果该元素不是根节点(不是代表元素),就一层一层访问父节点,直至根节点(找到集合的代表元素)。根节点的标志就是父节点是本身,要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。
合并
简单版
void merge(int i, int j)
{
fa[find(i)] = find(j);
}
合并操作也是很简单的,先找到两个集合的代表元素,然后将前者的父节点设为后者即可。当然也可以将后者的父节点设为前者。
最简单的并查集效率是比较低的。例如,来看下面这个场景:
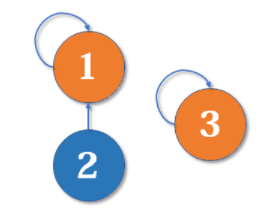
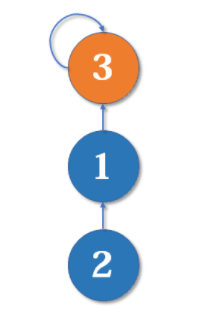
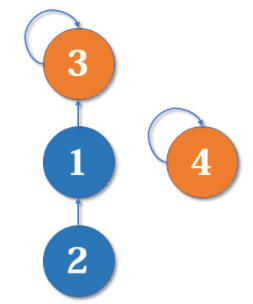
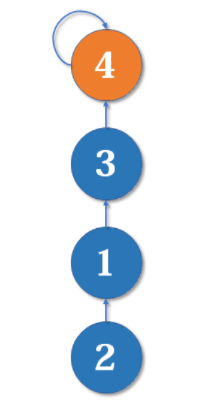
不断合并后,会出现如图所示的链状。随着链越来越长,我们想要从底部找到根节点会变得越来越难。
路径压缩
怎么解决呢?我们可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点,那我们希望每个元素到根节点的路径尽可能短,最好只需要一步,像这样:
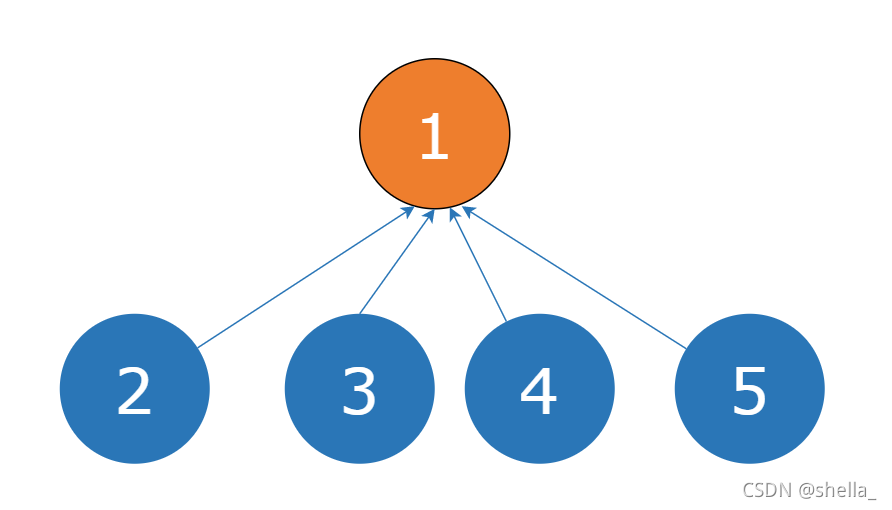
其实这说来也很好实现。只要我们在查询的过程中,把沿途的每个节点的父节点都设为根节点即可。下一次再查询时,我们就可以省很多事。这用递归的写法很容易实现,只需要调用一下find函数寻找根节点就行,此时fa [ ] :数组用来存储元素的根节点。
代码如下:
int find(int x)
{
if(x == fa[x])
return x;
else{
fa[x] = find(fa[x]); //父节点设为根节点(代表元素)
return fa[x]; //返回父节点
}
}
简写版,注意三目运算符加()。
int find(int x)
{
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
按秩合并
有些人可能有一个误解,以为路径压缩优化后,并查集始终都是一个菊花图(只有两层的树的俗称)。但其实,由于路径压缩只在查询时进行,也只压缩一条路径,所以并查集最终的结构仍然可能是比较复杂的。例如,现在我们有一棵较复杂的树需要与一个单元素的集合合并:
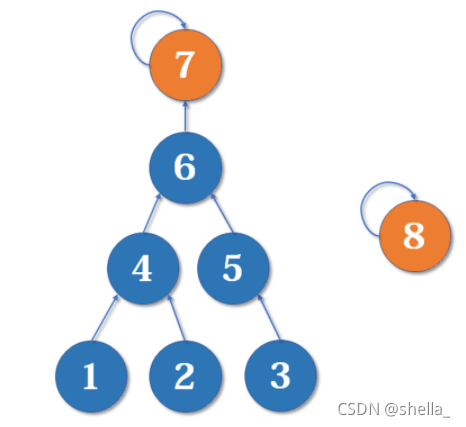
假如这时我们要merge(7,8),如果我们可以选择的话,是把7的父节点设为8好,还是把8的父节点设为7好呢?
当然是后者。因为如果把7的父节点设为8,会使树的深度(树中最长链的长度)加深,原来的树中每个元素到根节点的距离都变长了,之后我们寻找根节点的路径也就会相应变长。虽然我们有路径压缩,但路径压缩也是会消耗时间的。而把8的父节点设为7,则不会有这个问题,因为它没有影响到不相关的节点。
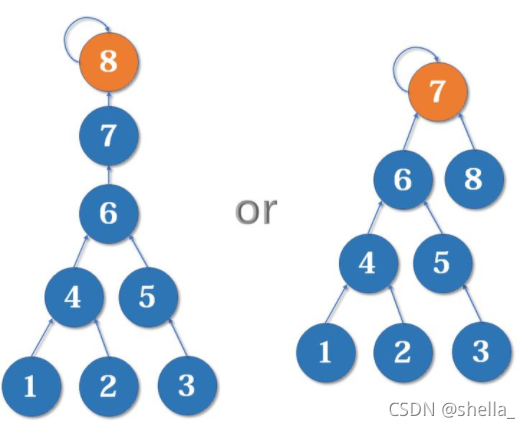
我们知道平衡树是便于搜索的,那么就像着这个方向进发!把深度较浅的树往深度较深的树上合并,从而使整棵树达到一个相对平衡的状态。
我们用一个数组rank[]记录每个根节点对应的树的深度(如果不是根节点,其rank相当于以它作为根节点的子树的深度,也就是集合的深度)。一开始,把所有元素的rank(秩)设为1。合并时比较两个根节点,把rank较小者往较大者上合并。
初始化(按秩合并)
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
{
fa[i] = i;
rank[i] = 1;
}
}
合并(按秩合并)
inline void merge(int i, int j)
{
int x = find(i), y = find(j); //先找到两个根节点
if (rank[x] <= rank[y])
fa[x] = y;
else
fa[y] = x;
if (rank[x] == rank[y] && x != y)
rank[y]++; //如果深度相同的树的合并,也就是一个深度相同的树作为另一棵树的子树,所以深度+1
}
关于并查集的应用,还有引入的亲戚问题,由于篇幅原因就不在此展示了,会另写一篇文章哦