一、前言
啥也不想说,就卷、卷技术;手撕红黑树搞起。
1、红黑树简介
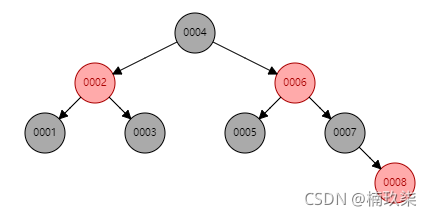
红黑树就是一种平衡的二叉查找树,其有五个特点:
1.每个节点要么是红?,要么是??;
2. 根节点?定是??的;
3. 每个叶?节点?定是??的NULL节点;
4. 如果?个节点是红?,那么它的左右?节点?定都是??的;
5. 从任意?个节点到叶?节点,所经过的??节点的数量?样多;
2、TreeMap简介
TreeMap 继承于AbstractMap ,其是一个 有序的key-value集合,内部基于
红黑树实现;
TreeMap 根据 其key的自然顺序进行排序,或者在构造方法中指定 Comparator 进行排序;
TreeMap的基本操作containsKey()、get()、put() 和 remove() 的时间复杂度是 log(n)。
另外,TreeMap是非同步的。 它的迭代器是fail-fast的。
二、put()方法
1、put操作实现原理
- 如果树为null,则构建一个TreeMapEntry设置为当前的root;
- 排序方式优先使用自定义比较器,找到要插入节点的父节点,然后插入;
- 执行
fixAfterInsertion(e)方法维护红黑树的平衡;
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
我们重点看一下红黑树的平衡是如何维护的
2、维护红黑树的平衡 – fixAfterInsertion()
建议大家细细拼,这一块还挺绕!!
新插入的节点颜色默认为红色。
平衡操作流程如下:
- 当节点不是跟节点且节点的父节点颜色为红色时进行while循环操作。
- 节点的父节点为爷爷节点的左子节点时;取爷爷节点的右子节点;
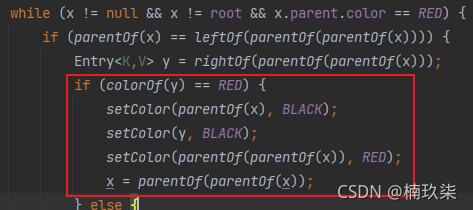
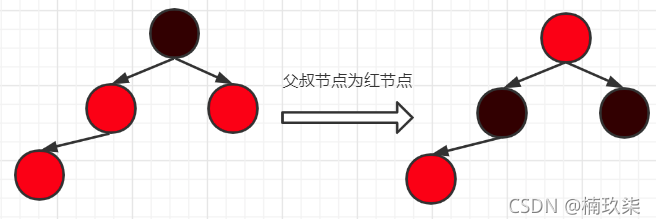
- 1)爷爷节点的右子节点颜色为红色时;
将爷爷节点的颜色改为红色,父节点和父节点的兄弟节点置为黑色;
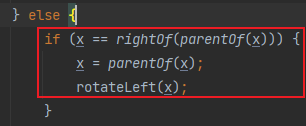
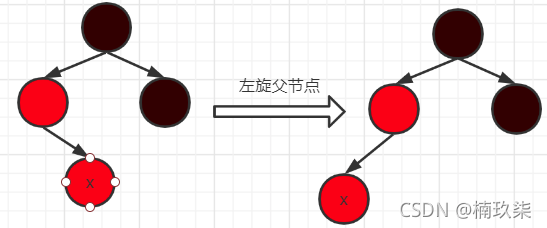
- 2)否则:
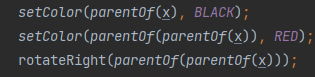
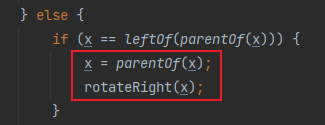
1、如果x是其父节点的右子节点:令当前节点为其父节点,接着执行左旋转操作;
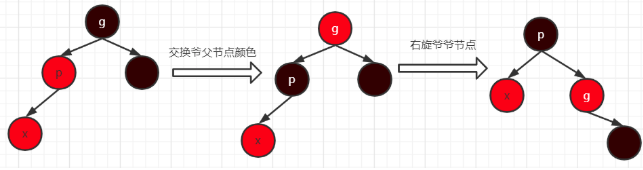
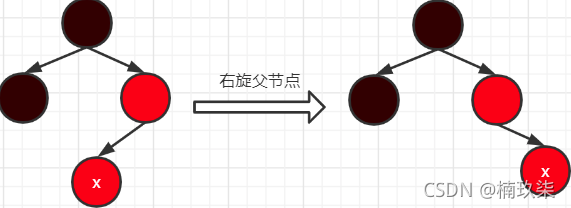
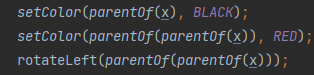
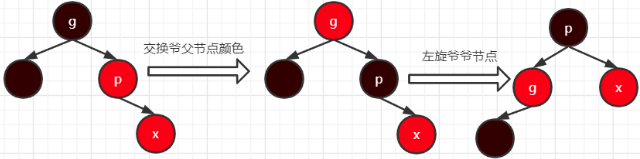
2、将x的父节点和爷爷节点的颜色对换。然后对爷爷节点进行右旋转;
- 节点的父节点为爷爷节点的右子节点时,取爷爷节点的左孩子;
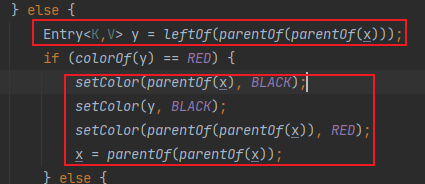
- 1)当爷爷节点的左子节点颜色为红色时;
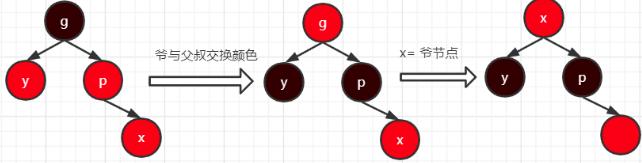
父节点和父节点的兄弟节点设置为黑色,爷爷节点设置为红色;
将爷爷节点作为新插入的节点x,遍历调整;
- 2)否则:
1、如果x是其父亲的左孩子:令x为其父节点,然后进行右旋操作;
2、将父节点设置为黑色,爷爷节点设置为红色,然后以爷爷节点为旋转点进行左旋转;
最后将根节点的颜色设置为黑色;
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
图解解决,我们接着手撕个红黑树的添加节点流程。
三、手撕红黑树添加节点
public class RedBlackTree<K extends Comparable<K>, V> {
public static void main(String[] args) {
RedBlackTree rdTree = new RedBlackTree();
rdTree.add(1, 1);
rdTree.add(3, 1);
rdTree.add(2, 1);
RedBlackTree.TreeNode root = rdTree.root;
System.out.println(root);
}
/**
* 判断节点指向父节点的连线的颜色 Red<-->true, Black<-->false
*/
private static final boolean RED = true;
private static final boolean BLACK = false;
/**
* 树节点
*/
class TreeNode {
public K key;
public V value;
public TreeNode left;
public TreeNode right;
public boolean color;
public TreeNode(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
this.color = RED;
}
}
private TreeNode root;
private int size;
public RedBlackTree() {
root = null;
size = 0;
}
/**
* 判断一个树节点是否是红节点。
*
* @param node 树节点
*/
public boolean isRed(TreeNode node) {
if (node == null) {
return BLACK;
}
return node.color;
}
public void add(K key, V value) {
root = add(root, key, value);
root.color = BLACK;
}
public TreeNode add(TreeNode node, K key, V value) {
if (node == null) {
size++;
return new TreeNode(key, value);
}
// 1.往树中添加节点
if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
node.right = add(node.right, key, value);
} else {
node.value = value;
}
// 2.维护红黑树的结构
// 2.1 如果node节点的右子节点为红色的,而左子节点不是红色的,左旋转
if (isRed(node.right) && !isRed(node.left)) {
node = leftRotate(node);
}
// 2.2 如果node节点的左子节点、左子节点的左子节点是红色的,右旋转
if (isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
// 2.3 如果node节点的左子节点和右子节点都是红节点,则颜色翻转
if (isRed(node.left) && isRed(node.right) && !isRed(node)) {
flipColor(node);
}
return node;
}
/**
* 左旋转
* node x
* / \ 左旋转 / \
* T1 x ---------> node T3
* / \ / \
* T2 T3 T1 T2
*/
private TreeNode leftRotate(TreeNode node) {
TreeNode x = node.right;
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
/**
* 右旋转
* node x
* / \ 右旋转 / \
* x T3 ---------> T1 node
* / \ / \
* T1 T2 T2 T3
*/
private TreeNode rightRotate(TreeNode node) {
TreeNode x = node.left;
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
/**
* 颜色翻转
* 如果一个节点的颜色为黑色,而它左右子节点的颜色为红色。
* 则将其的颜色置为红色,其子节点的颜色置为黑色。
*/
private void flipColor(TreeNode node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
}
只要我们技术足够卷、没有hold不住的技术面,奥利给!