LeetCode 105. 从前序与中序遍历序列构造二叉树

1. 题目描述

给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
示例 1:

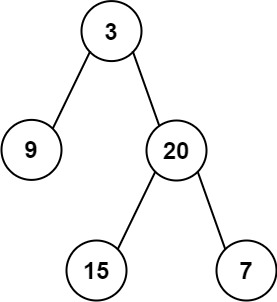
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

2. 题解：

方法：深度优先遍历、递归
先递归创建左右子树，再创建根节点，并将指针指向根的左右子树。

具体步骤如下：

先序遍历找到根节点：先序遍历第一个点，就是根节点；
在中序遍历中找到根节点的位置K， K的左边是左子树的中序遍历， K的右边是右子树的中序遍历；
长度的利用：假设中序遍历中左子树的长度为L，则先序遍历中1~L+1 是左子树后边则是右子树；
有了中序遍历和先序遍历，可以先创建左右子树，在创建根节点；

时间复杂度： 在初始化时，哈希映射 unordered_map<int,int> pos, 这样可以O（1）的时间度找到先序遍历中根节点在中序遍历中的位置，创建每个结点的时间是O（1），所以时间复杂度是O（N）；
空间复杂度： O（N），除了返回的数组空间是N以外，还有递归的深度H，但H < N ,所以总空间复杂度依旧是O（N）。

C++ ：

class Solution {
public:
//1.判定父节点与子节点 ：利用好先序与中序遍历
//2.null : 特判情况
    unordered_map<int, int> pos ;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size() ;
        for (int i = 0; i < n; i++ ) {
            pos[inorder[i]] = i ; //用 map 记录每个值在中序遍历中的位置 
        }
        return dfs(preorder, inorder, 0, n-1, 0, n-1 ) ;
    }

    TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir) {
        if (pl > pr) return nullptr ; // 特判
        int k = pos[pre[pl]] - il ; //左子树的长度 = 先序遍历根节点的位置映射在中序遍历中 - 中序遍历的第一个结点
        TreeNode* root = new TreeNode(pre[pl]) ; //当前树的根节点
        root->left = dfs(pre, in , pl+1, pl+k, il, il+k-1) ; // 先序遍历从第一个左子树结点 到 最后一个左子树结点 中序遍历中第一个左子树结点 到根节点之前一个
        root->right = dfs(pre, in, pl+k+1, pr, il+k+1 , ir ) ;
        return root ;
    }
};

Golang：

func buildTree(preorder []int, inorder []int) *TreeNode {
    if len(preorder) == 0 {
        return nil 
    }
    value := preorder[0] //存储根节点 
    root := &TreeNode{Val: value} 
    i:= 0 
    for ; i < len(preorder); i++ {
        if inorder[i] == value { // 遍历中序二叉树， 若该店为value即根值， 则计算左右子树
            root.Left = buildTree(preorder[1:1+i], inorder[:i] ) 
            root.Right = buildTree(preorder[1+i: ], inorder[i+1 :] )
            break
        }
    } 
    return root 
}