主旨思想

分治思想主旨就是“分而治之”，大概就是指将一个规模较大的问题分割成规模较小的同类问题，然后再将这些小的子问题，逐个解决，最终大问题也就解决掉了。通常分治和递归是一起用的。

例题

二分法查找

二分法查找算法是一种提现分治思想的算法。
力扣题目链接：704. 二分查找
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:
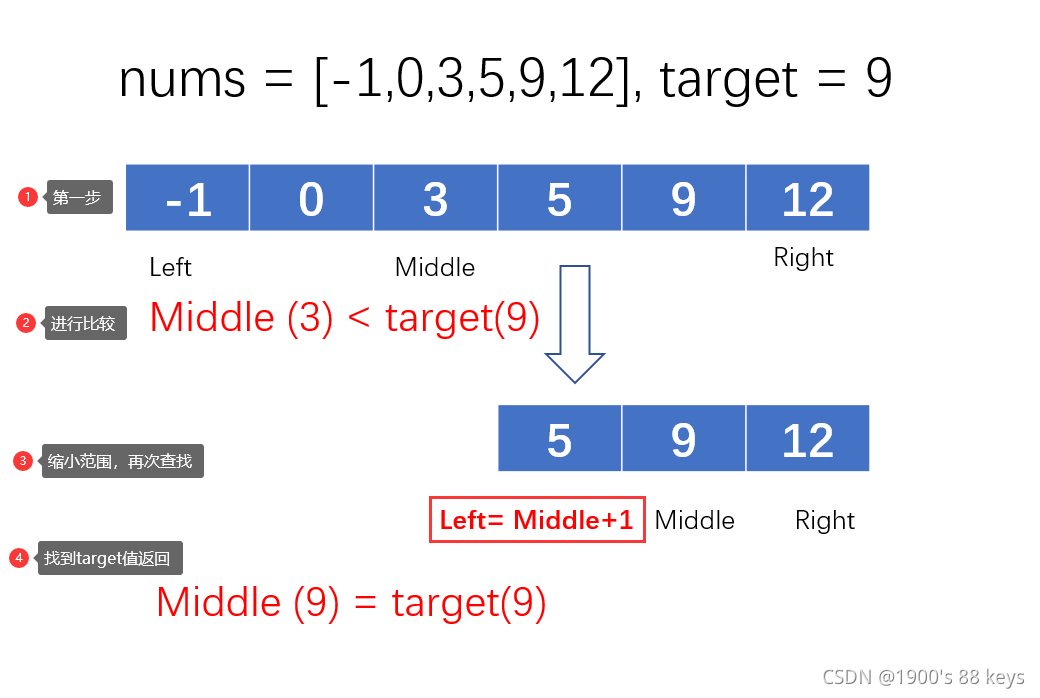
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-search
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

二分法查找算法的思路的前提是数组有序的，将上面数组从中间一分为二，然后用中间middle值和target目标值进行比较：

如果中间的数大于target目标值，那么target就可能在左边数组当中，然后把中间middle-1赋值给右边right的值，再从左边数组中寻找新的中间middle值和target目标值进行比较
如果中间的数小于target目标值，那么target就在可能右边数组当中，然后把中间middle+1赋值给左边left的值，再从边数组中寻找新的中间middle值和target目标值进行比较

例如示例 1:中用图表示：

在这里插入图片描述

非递归写法

javascript：

var search = function(nums, target) {
    let left = 0, right = nums.length-1;//定义左右边界[left,right]
    while(left <= right)//当left = right,依然是在[left,right]区间当中
    {
        let mid =left + Math.floor((right - left)/2);//计算中间值，防止溢出，等效于(left+right)/2，后面这种写法可能会导致溢出如果right特别大，但是没有越界，left特别大，但也没有越界，但是你把他俩相加就有可能越界。
        if(nums[mid] > target)
        {
            right = mid - 1;//target可能在左区间[left,mid - 1]之间，所以更新右边界right = mid - 1;
        }
        else if(nums[mid] < target)
        {
            left = mid + 1;//target可能在右区间[mid + 1,right]之间，所以更新左边界边left = mid + 1;
        }
        else//(nums[mid] ==  target)
        {
            return mid;//找到目标值，返回结果
        }
    }
    return -1;//没有找到目标值，按题意返回-1
};

递归写法

int recursion(int *nums, int target, int left, int right)
{
    if(left > right)
    {
        return -1;//递归出口，没有找到值
    }
    else
    {    
        int mid = left + (right - left)/2;
        if(target < nums[mid])
        {
            return recursion(nums, target, left, mid - 1);
        }
        else if(target >  nums[mid])
        {
            return recursion(nums, target, mid + 1, right);
        }
        else
        {
            return mid;
        }
    }
}
int search(int* nums, int numsSize, int target){
    int left = 0, right = numsSize - 1;
    return recursion(nums, target, left,  right);//调用递归，并且把值返回出去。
}

快速排序算法

基本思想

快速排序用到了分而治之的思想。

先从数组中找到一个数，可以是是任取待排序序列的一个元素作为中心元素(可以用第一个，最后一个，也可以是中间任何一个)，习惯将其称为pivot枢轴元素；
用pivot将数组分成两个数组：
- 将所有小于pivot的数放在其左边；
- 将所有大于pivot的数在其右边；
然后对两个新的数组按照上面的算法继续排序。

例如：
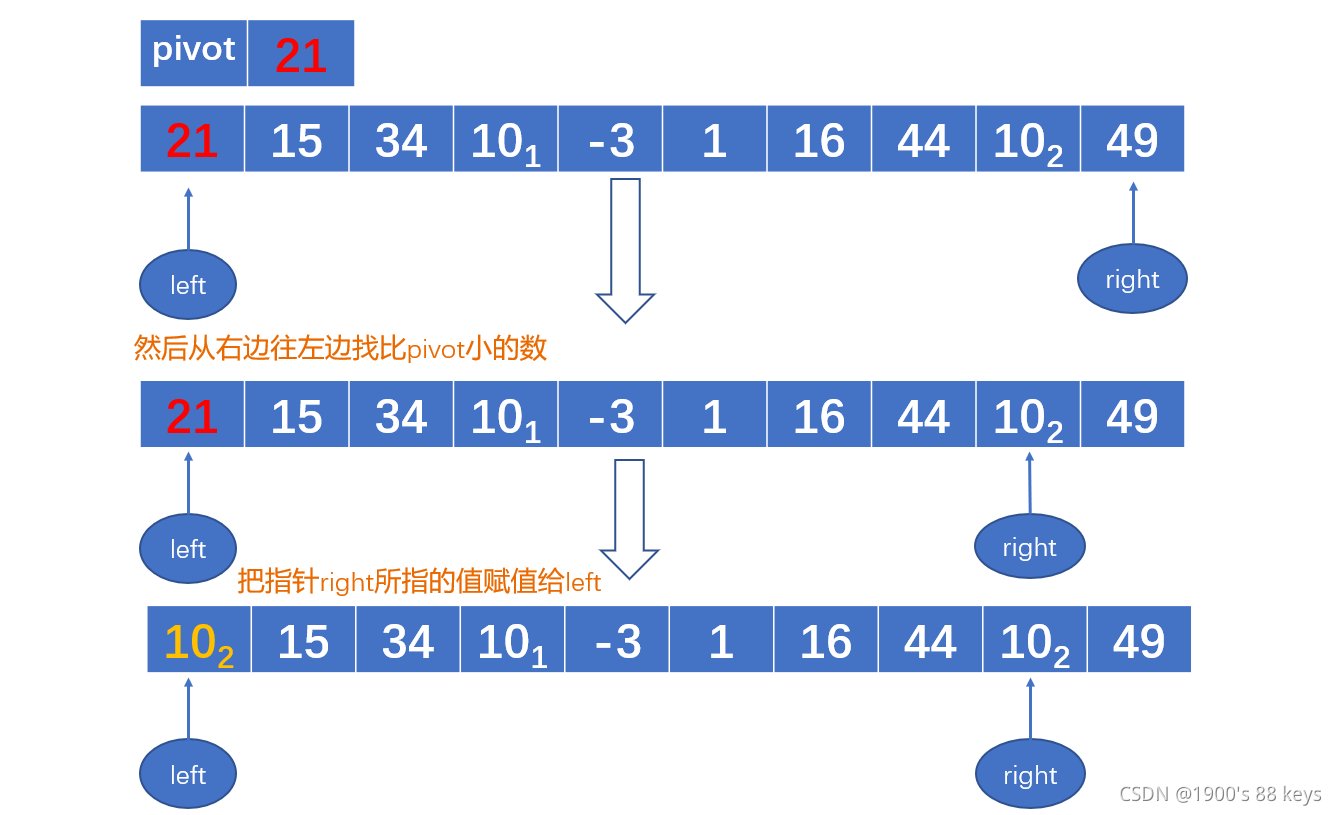
数组 [ 21, 15, 34 , 10, -3, 1 , 16 , 44, 10, 49];

定义一枢轴元素pivot，即为21；
定义一左边指针的为left;
定义一右边指针的为right。
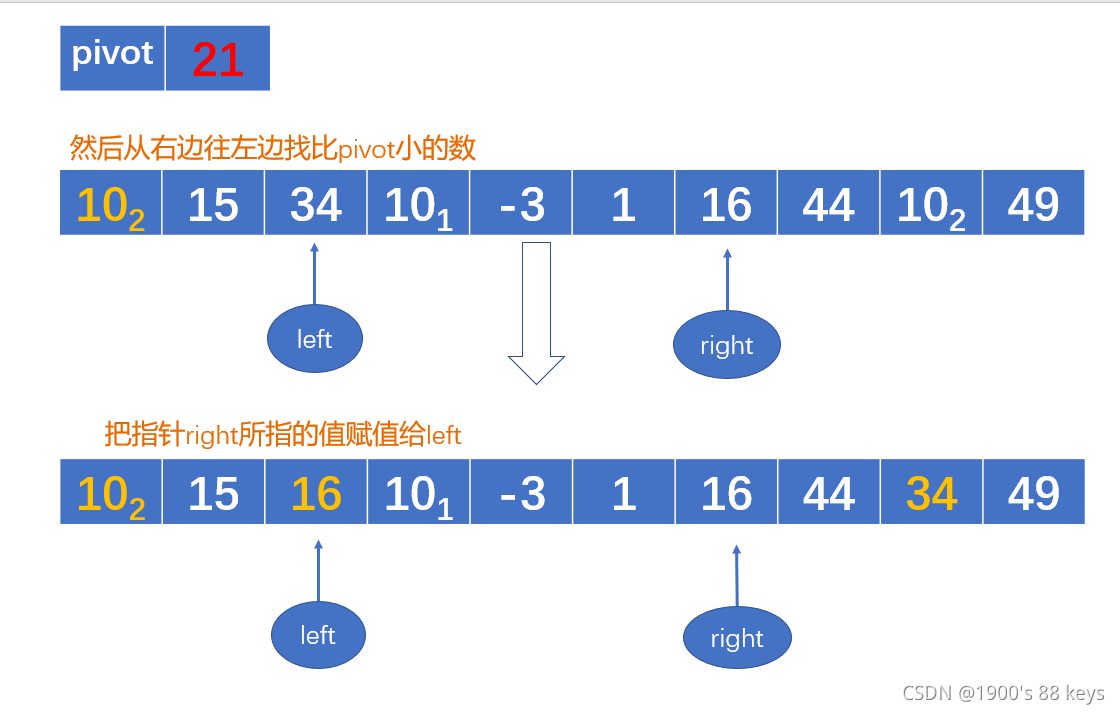
然后从右边往左边找比pivot小的数
把指针right所指的值赋值给left

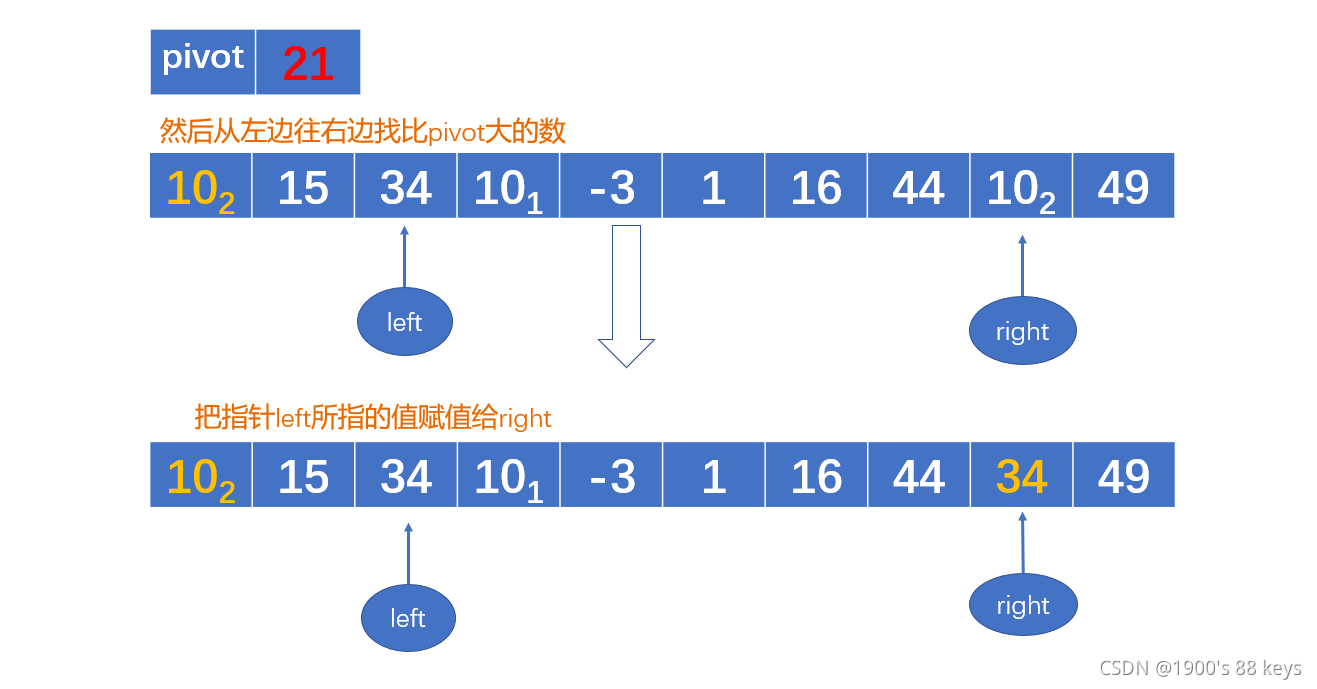
在这里插入图片描述

直到
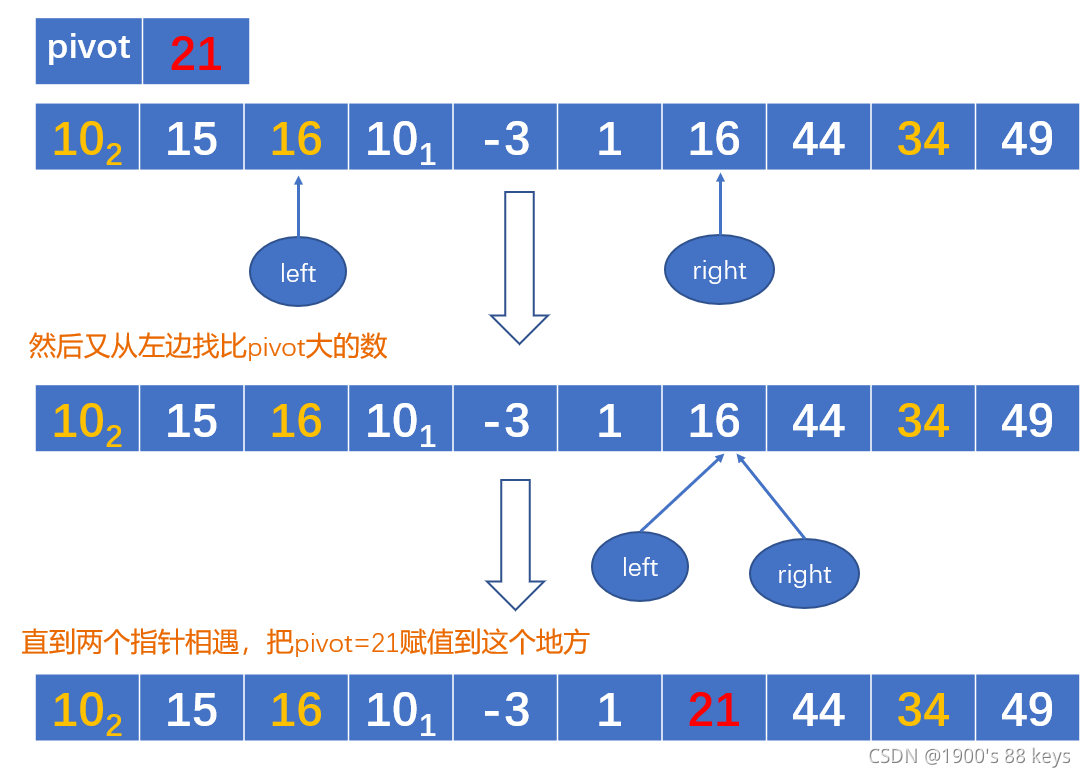
在这里插入图片描述
这样第一趟的排序就完成了，通过pivot将数组分成了[10,15,16,10，-3,1] 与 [44, 34, 49]左右两部分，然后分别对这两个数组重新用相同的算法，直到只剩下一个元素。

代码

javascript:

function partition(arr, left, right) {
    var pivot = arr[left];//初始化pivot为数组第一个数；
    while (left < right) {//只要left还小于right就进行循环；
        while (left < right && arr[right] >= pivot) {//先从右边找一个比枢轴元素pivot小的数
            right--;
        }
        arr[left] = arr[right];//将当前left所指的数赋值给right
        while (left < right && arr[left] <= pivot) {//从左边找一个比枢轴元素pivot大的数
            left++;
        }
        arr[right] = arr[left];//将当前right所指的数赋值给left
    }
    arr[right] = pivot;//将pivot值赋值给当前right
    return right;//返回索引
}
function quickSort(arr, left, right) {
	var middle;
    if (left < right) {
    	middle = partition(arr, left, right);//如果left比right小，进行一次划分，将返回来的值赋值给middle；
        partition(arr, mid + 1, right);//对middle + 1到right的部分进行一次快排（递归进行）
        partition(arr, left, mid - 1);//对left到middle - 1的部分进行一次快排（递归进行）
    }
}

/*------------------------测试代码-----------------------------------*/

var arr =  [ 21, 15, 34 , 10, -3, 1 , 16 , 44, 10, 49];
console.log("排序前的数组：", arr)


quickSort(arr, 0, arr.length - 1);
console.log("排序后的数组", arr);

在这里插入图片描述

时间和空间复杂度分析

时间复杂度：

理想的情况：时间复杂度为O(nlogn)
最坏情况：O(n²),这种情况是退化成冒泡排序

**空间复杂度：**根据实现的方式不同而不同
稳定性：不稳定

归并算法

基本思想

归并算法也是分而治之的思想(分治法) 。
例子
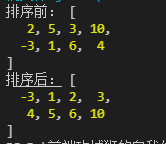
输入数组 [ 2, 5, 3 , 10, -3, 1 , 6 , 4]；
分治思想如下：
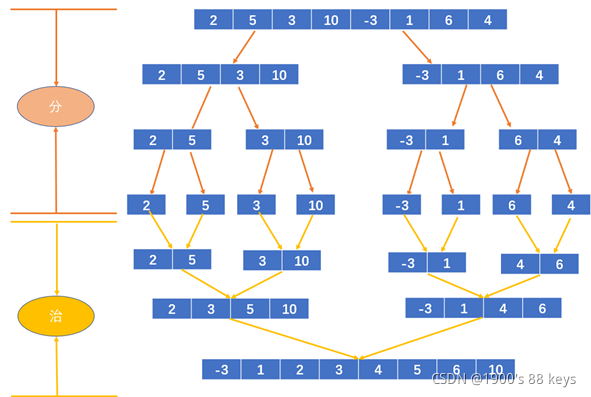
在这里插入图片描述

代码

function merge(arr, left, mid, right, temp) {
    var i = left;
    var j = mid + 1;
    var t = 0;
    while (i <= mid || j <= right) {
        if (i > mid) {
            temp[t++] = arr[j++];
        }
        else if (j > right) {
            temp[t++] = arr[i++];
        }
        else {
            if (arr[i] <= arr[j]) {
                temp[t++] = arr[i++];
            }
            else {
                temp[t++] = arr[j++];
            }
        }
    }
    var k = left;
    t = 0;
    while (k <= right) {
        arr[k++] = temp[t++]
    }
}

function mergeSort(arr, left, right, temp) {
    if (left < right) {
        var mid = Math.floor((left + right) / 2);//中间索引
        mergeSort(arr, left, mid, temp);//左边递归分解
        mergeSort(arr, mid + 1, right, temp);//右边递归分解
        merge(arr, left, mid, right, temp);//合并
    }
}
/*------------------------测试代码--------------------*/

var arr = [2, 5, 3, 10, -3, 1, 6, 4];
var temp = new Array(arr.length);
console.log("排序前：", arr);
mergeSort(arr, 0, arr.length - 1, temp);
console.log("排序后：", arr);