一. 快速排序

??快速是一个简单且直观的排序算法，主要的算法思想就是，在一个未排好序的序列中找出最小的值，并把它放在该序列的最前面。
如图所示：
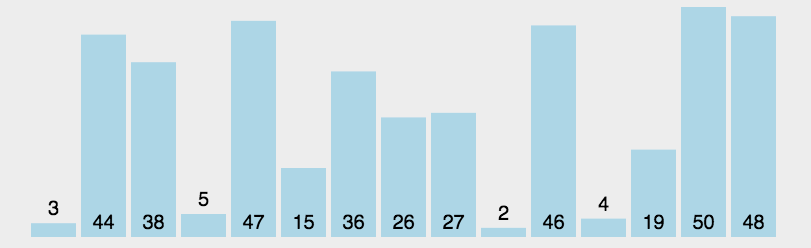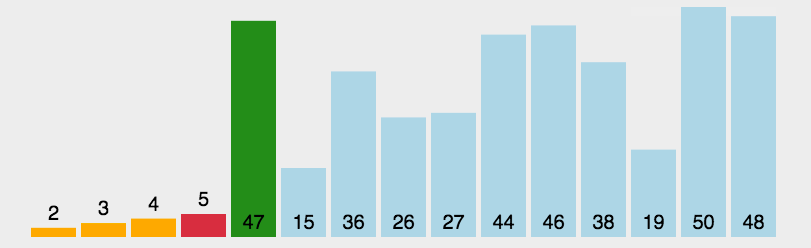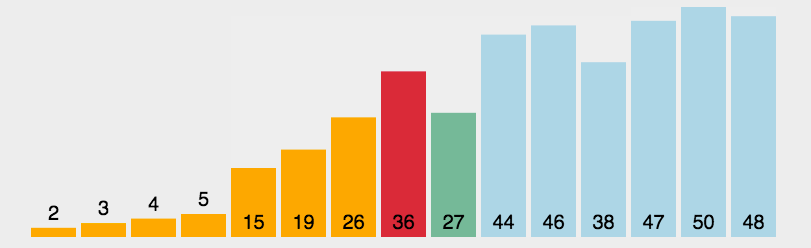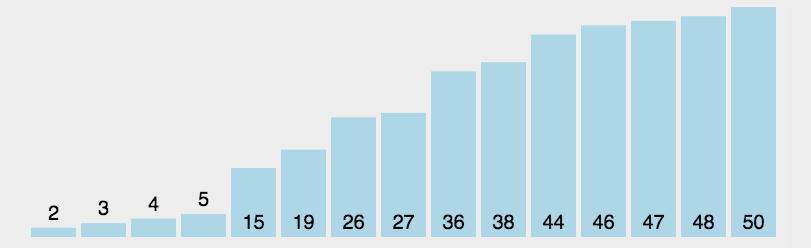
请添加图片描述
每一次排序都将该序列的最小的值放在最前面，然后再继续找出后面的序列中的最小值，也就是总序列的第二小值，以此类推，达到升序的效果。
代码如下：

void SelectionSort(int* arr, int arrSize){
    for(int i = 0; i < arrSize - 1; i++){
        int min = i;
        for(int j = i; j < arrSize; j++){
            if(arr[j] < arr[min]){
                min = j;
            }
        }
        swap(&arr[i], &arr[min]);
    }
}

二. 课后练习

2.1 有效三角形的个数

题目链接：

611. 有效三角形的个数

思路分析：

根据三角型定理，我们知道两边相加要大于第三边，但考虑到数据为0的情况，比如0，1，0，0 + 1 > 0，所以我们要先对其进行快速排序，将较短的两边相加与第三边进行比较。这道题如果用普通的遍历方法很容易超时，所以我们要用二分的方法。

但肯定很多人疑惑，为什么能够用二分，我们仔细思考一番，当我们排好序后，并且确认好了两条较短的边 i 和 j，那我们只要找到满足m > i + j条件中的最大的一个m，那其前面的肯定也是可以的。

在这里插入图片描述

代码如下：

void swap(int* a, int* b){
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void SelectionSort(int* arr, int arrSize){
    for(int i = 0; i < arrSize - 1; i++){
        int min = i;
        for(int j = i; j < arrSize; j++){
            if(arr[j] < arr[min]){
                min = j;
            }
        }
        swap(&arr[i], &arr[min]);
    }
}

int triangleNumber(int* nums, int numsSize){
    int count = 0;
    SelectionSort(nums, numsSize);
    for(int i = 0; i < numsSize - 2; i++){
        for(int j = i + 1; j < numsSize - 1; j++){
            int left = j + 1,right = numsSize - 1, k = j;
            while(left <= right){
                int mid = (left + right) / 2;
                if(nums[mid] < nums[i] + nums[j]){
                    k = mid;
                    left = mid + 1;
                }
                else{
                    right = mid - 1;
                }
            }
            //printf("%d ", k);
            count += k - j;
        }
        
    }
    return count;
}