七、图
图的基本概念
1.图:图G由两个集合V和E组成,记为G=(V,E),其中V是顶点的有穷非空集合,E是由V中顶点的序偶组成的有穷集,这些序偶称为边或弧.
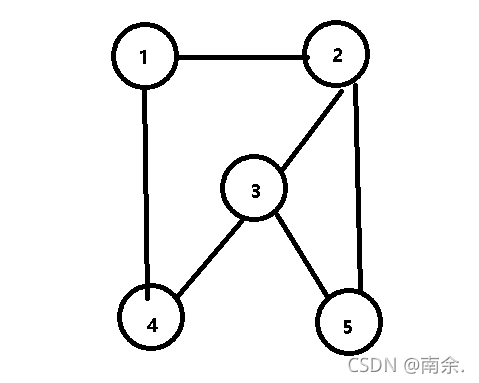
2.无向图
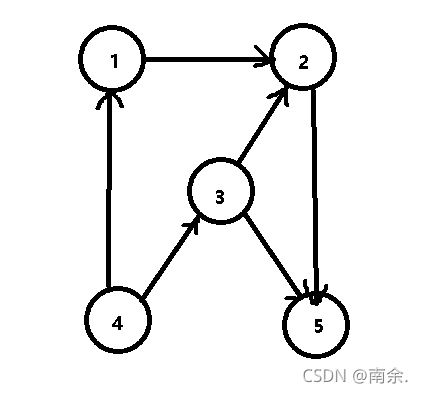
3.有向图
4.完全图:如果任意两个顶点之间都存在边,则称该图为无向完全图
至少存在以下条边(示例):

5.顶点的度、入度、出度
度=入度+出度
TD(v) = ID(V) + OD(V)
入度:以顶点V为头的弧的数目称为V的入度.
出度:以顶点V为尾的弧的数目称为V的出度.
6.子图
有向图所有顶点:出度之和=入度之和
7.连通、连通图和连通分量
!路径≠边
任何连通图的连通分量只有一个,即是自身;
对于有n个顶点无向图,至少有n-1条边才能连通
8.强连通图、强连通分量
有n个顶点至少需要n条边才能强连通
图的存储
存储方式:领接矩阵、领接表、逆领接表、十字链表和领接多重表
一、领接矩阵(二维数组)
邻接矩阵:表示图中结点之间关系的矩阵称为邻接矩阵.
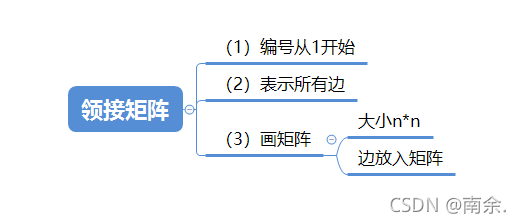
.特点
(1) 无向图的领接矩阵是对称矩阵
(2) 无向图的领接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的度TD(Vi)
(3) 有向图的领接矩阵的第i行(或第i列)非零元素的个数正好是第i个顶点的出度OD(Vi)(或入度ID(Vi))
(4) 稠密图适合使用领接矩阵法存储
二、领接表(存储图的出度)有向图
邻接表:由顶点数据表和表示数据关系的边(弧)构成的表.
N:顶点,e:边

三、 图的遍历
1.广度优先搜索(BFS)每走一次访问一批结点
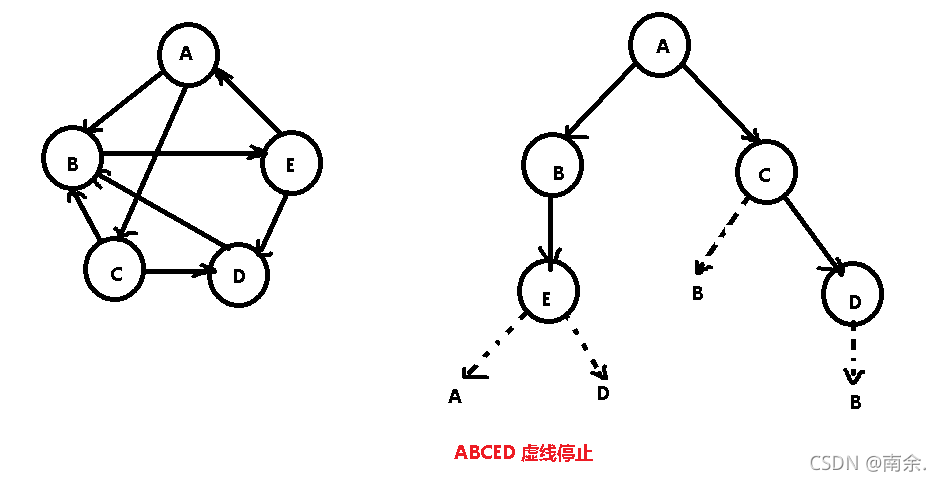
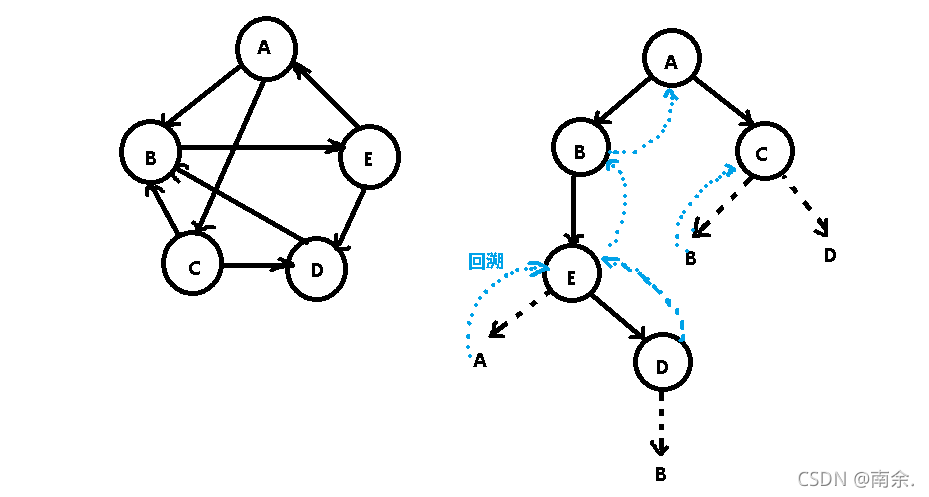
2.深度优先搜索(DFS)一次走到底,无路可走则回溯
四、 最小(代价)生成树

1.Prim算法(找权值最小的整体)
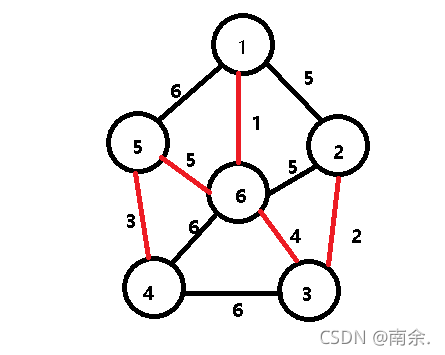
2.Kruskal算法(求权值最小的边,连通为止)同上。

五、拓扑排序
拓扑排序:由某个集合上的一个偏序得到该集合上一个全序的操作称为拓扑排序.
前提: 有向无环图(DAG),即每次删除入度为0的顶点并输出之

判断题
边很少的图称为稀疏图,反之称为稠密图(√)
有向图中,所有顶点的入度与出度的和等于边个数的2倍.(√)
图的存储方法:邻接矩阵,邻接表,邻接多重表,十字链表和边集数组.(√)
图的深度优先搜索类似于树的先根遍历(√)
图的广度优先搜索类似于树的层次遍历.(√)
选择题
1.以下有关有向图的说法正确的是?()
A.强连接图中任何顶点到其他所有顶点都有弧
B.有向完全图一定是强连通图
C.有向完全图中某顶点的入度等于出度
D.有向图边集的子集和顶点集的子集可构成原有图的子图
答案:B
2.在一个图中,所有顶点的度数之和等于所有边数的__倍?()
A.1/2
B.1
C.2
D.4
答案:C
3.具有100个顶点的连通图,至少需要()条边?
A.99
B.100
C.101
D.102
答案:A
八、查找
1.查找:根据给定的关键字的值,检索某个与该值相等的数据元素是否在查找表中,找到为查找成功,找不到为查找失败.
2.平均查找长度(ASL):
查找的长度是指需要比较的关键字次数,平均查找长度则是所有查找过程中进行关键字的比较次数的平均值
ASL=总查找次数/元素个数
一、顺序查找
顺序查找平均查找长度为:ASL = n+1/2
二、折半查找
折半查找平均查找长度为:ASL = log2(n+1)
二叉排序树:左子树<根<右子树
代码如下(示例)
BstTree BstSearch(BstTree bst,DataType x){
if(bst==Null)
return Null;
else if(bst->data==x) //根==x
return bst;
else if(x<bst->data) //x<根
return BstSearch(bst->lchild , x); //查找左子树
else(x>bst->data) // x>根
return BstSearch(bst->rchild , x) //查找右子树
}
哈希表
1.常用hash函数的构造方法

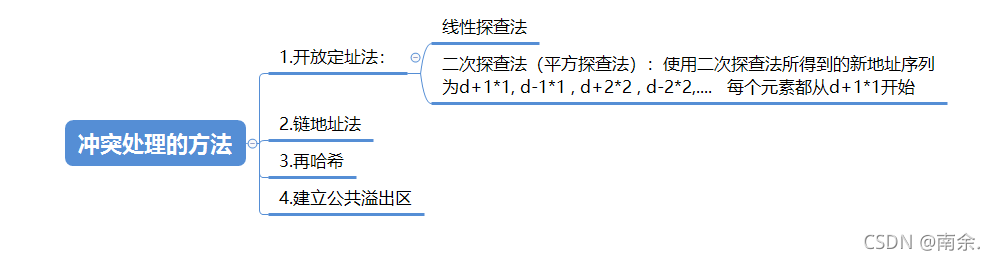
2.冲突处理的方法
多选题
1.哈希函数的构造方法有()
A.直接定址法
B.数字分析法
C.平方取中法,折叠法
D.除留余数法和随机数法
答案:ABCD
2.哈希函数处理冲突的方法有()
A.开放地址法
B.再哈希法
C.链地址法和建立一个公共溢出区.
D.平方取中法
答案:ABC
判断题
查找表是由同一类型的数据元素或记录构成的集合.(√)
静态查找表查询某个特定的数据元素是否在查找表中,可以检索某个特定的数据元素的各种属性.(√)
动态查找表在查找过程中同时插入查找不存在的数据元素,或者能从查找表中删除已存在的某个数据元素..(√)
两个不同的关键字,其散列函数值相同,因而被映射到同一表位置的现象称为冲突.(√)
九、排序
1.排序:就是按关键字值的递增或递减的次序,把文件中的各记录一次排列起来,可使一个无序文件变成有序文件的一种操作.

排序算法的稳定性:相同元素排序前后的相对位置没有发生变化,则为稳定,反之为不稳定.
内部排序:在排序过程中,所有待排序记录都放在内存中进行的排序称为内部排序.
外部排序:当待排序的记录很多,排序时不仅要使用内存,而且还要使用外部存储器的排序方法称为外部排序.
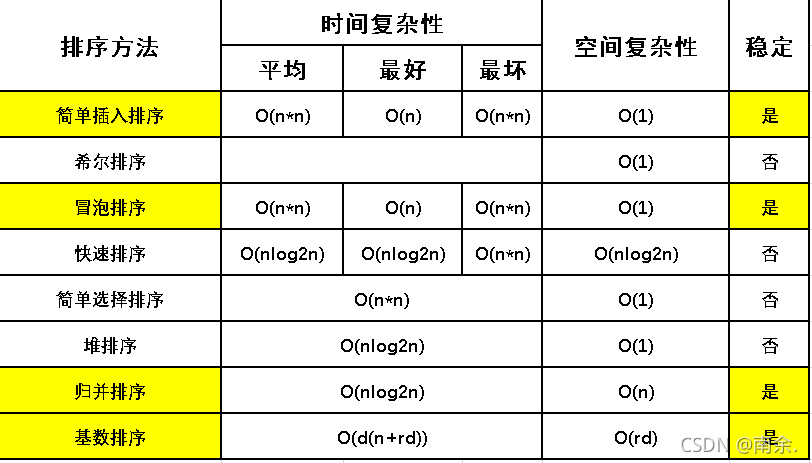
各种排序方法比较