1. 动态规划

基本思想：
问题的最优解如果可以由子问题的最优解推导得到，则可以先求解子问题的最优解，在构造原问题的最优解；若子问题有较多的重复出现，则可以自底向上从最终子问题向原问题逐步求解。
动态规划特点：
1.重叠子问题；
2.状态转移方程；
3.最优子结构；

动态规划（Dynamic Programming）解题方法：

1.将原问题分解为子问题 (注意:1,子问题与原问题形式相同或类似,只是问题规模变小了,从而变简单了; 2,子问题一旦求出就要保存下来,保证每个子问题只求解一遍)
2.确定状态(状态:在动规解题中,我们将和子问题相关的各个变量的一组取值,称之为一个"状态",一个状态对应一个或多个子问题所谓的在某个状态的值,这个就是状态所对应的子问题的解,所有状态的集合称为"状态空间".我的理解就是状态就是某个问题某组变量,状态空间就是该问题的所有组变量) 另外:整个问题的时间复杂度就是状态数目乘以每个状态所需要的时间
3.确定一些初始状态(边界条件)的值 (这个视情况而定,千万别以为就是最简单的那个子问题解,上面只是例子,真正实践动规千变万化)
4.确定状态转移方程 (这一步和第三步是最关键的 记住"人人为我"递推,由已知推未知)

例题：数字三角形：
给定一个数字三角形，找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上。
[2],
[3,4],
[6,5,7],
[4,1,8,3]
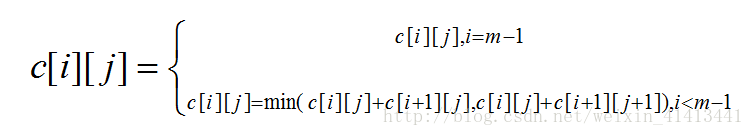
在这里插入图片描述

class Solution {
public:
    /**
     * @param triangle: a list of lists of integers
     * @return: An integer, minimum path sum
     */
     
    int minimumTotal(vector<vector<int>> &triangle) {
        // write your code here
        int r=triangle.size(); //行
        int c=triangle[r-1].size();  //列
        if(r==0&&c==0)
        return 0;
        int D[r][c];
      //  int Min[r][c];
        for(int i=0;i<c;i++)
        D[r-1][i]=triangle[r-1][i];
        
        for(int i=r-2;i>=0;i--)
            for(int j=0;j<=i;j++)
            D[i][j]=min(D[i+1][j],D[i+1][j+1])+triangle[i][j];
           return D[0][0];
    }
};