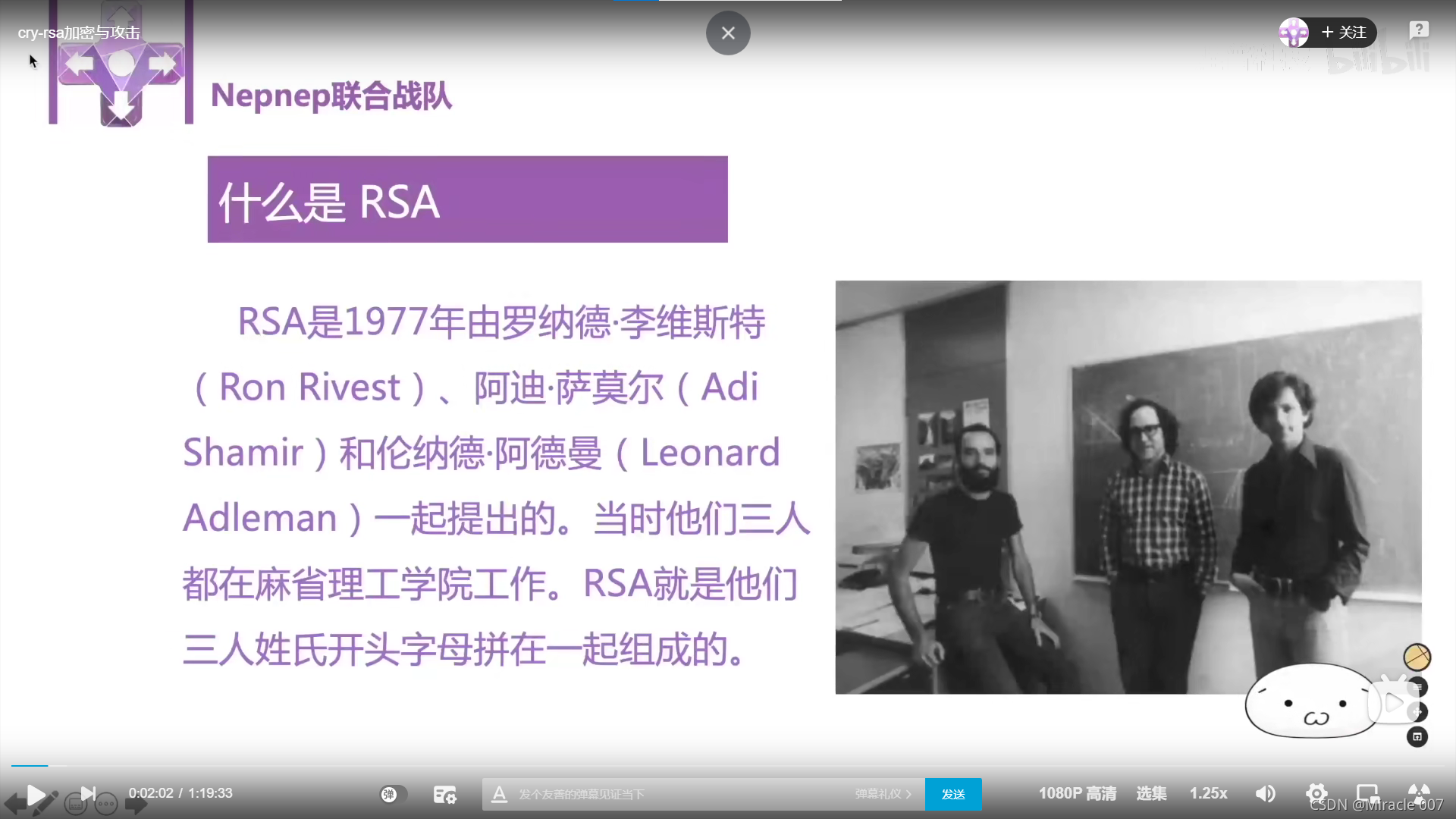
一、什么是RSA
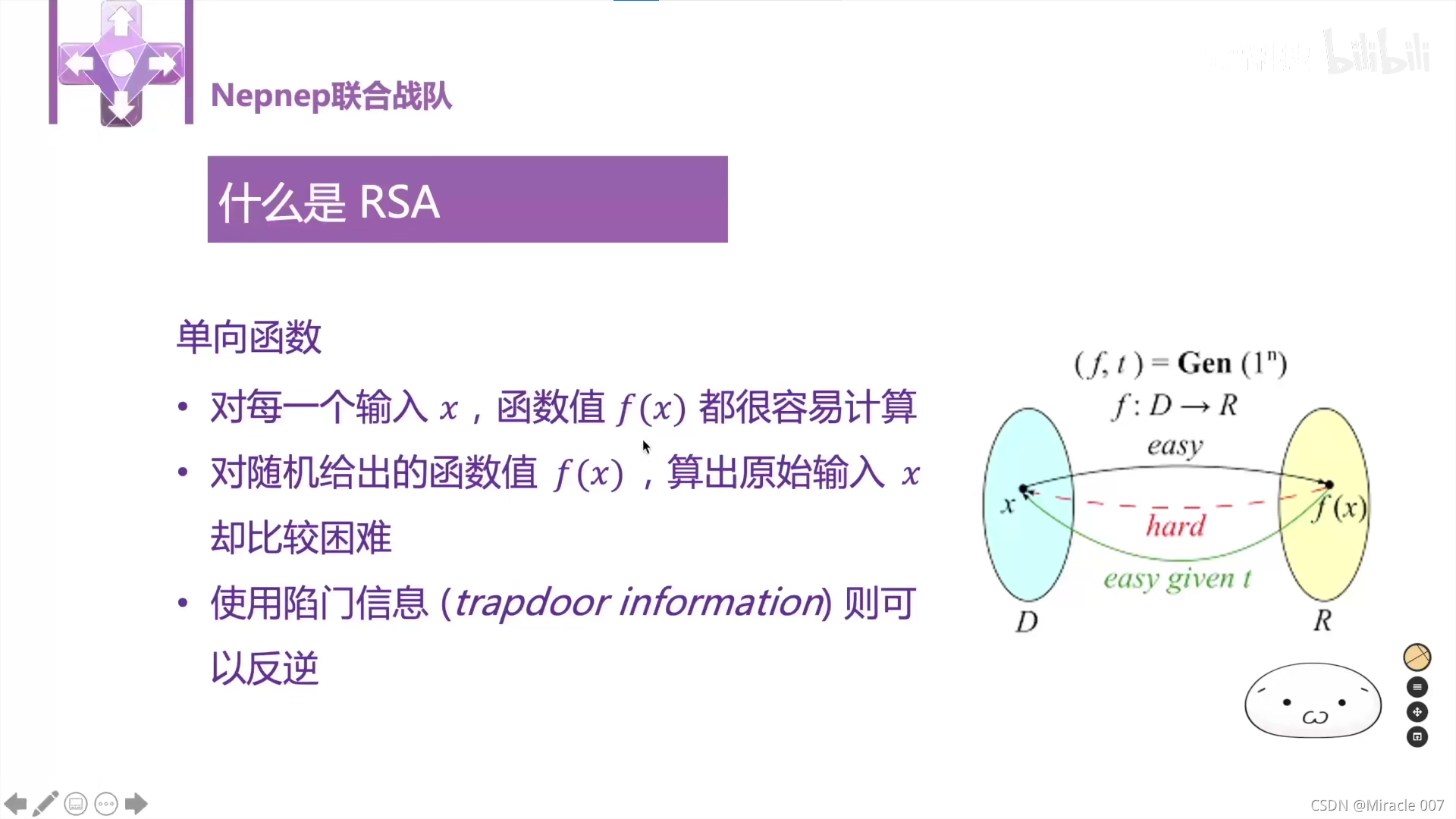
加密算法一般认为是可以加密和解密的,所以哈希不是加密算法,因为它不可逆,不能解密。
二、一点点数论基础

a和b除以m取余算出来的结果一定是一样的

推论一是快速幂算法的理论基础。

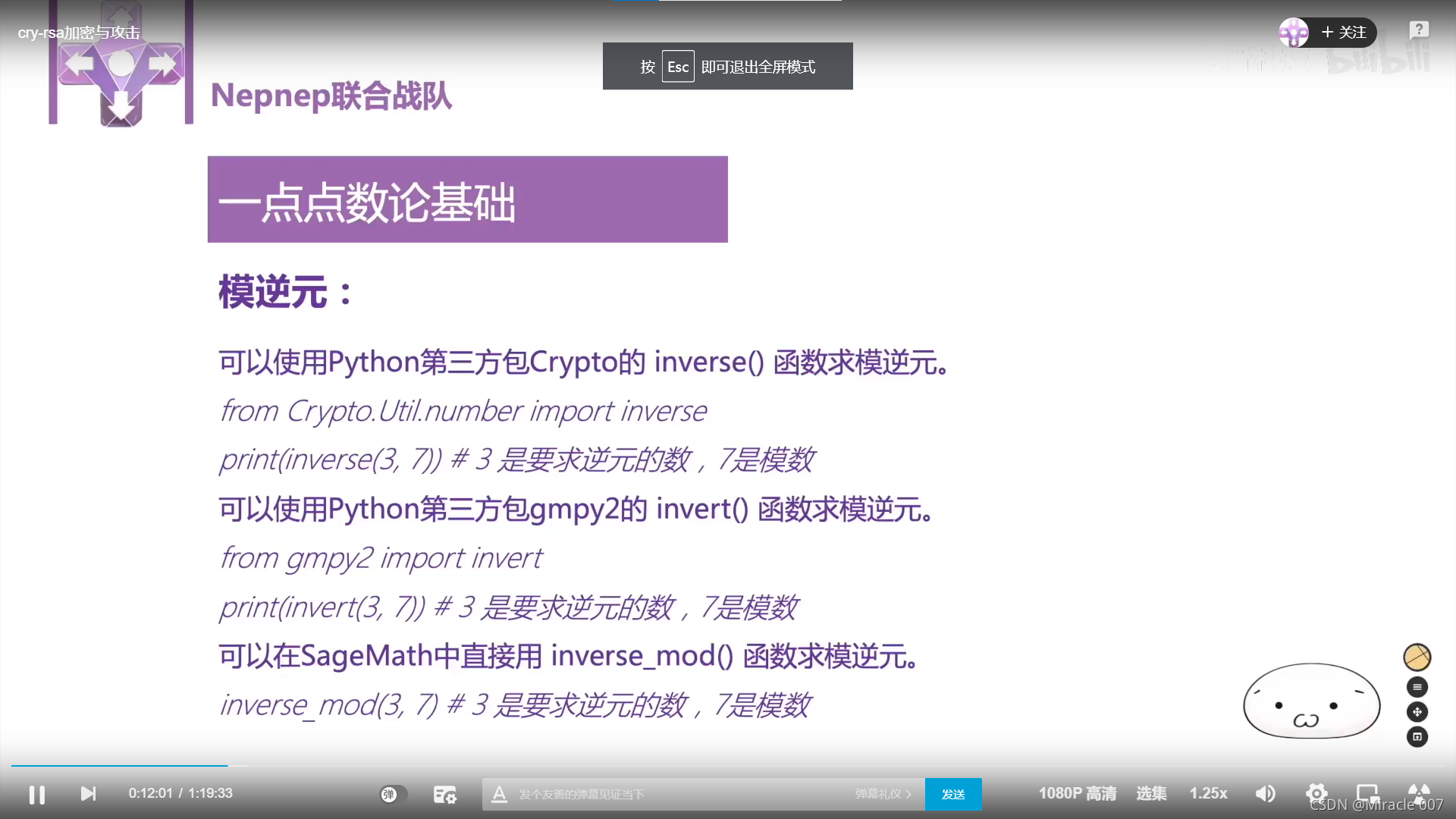
模逆元和同余


欧拉函数

互素的个数。



欧拉定理要记住。
费马小定理是欧拉定理的一个特殊情况
三、RSA是如何加密和解密的



python实现
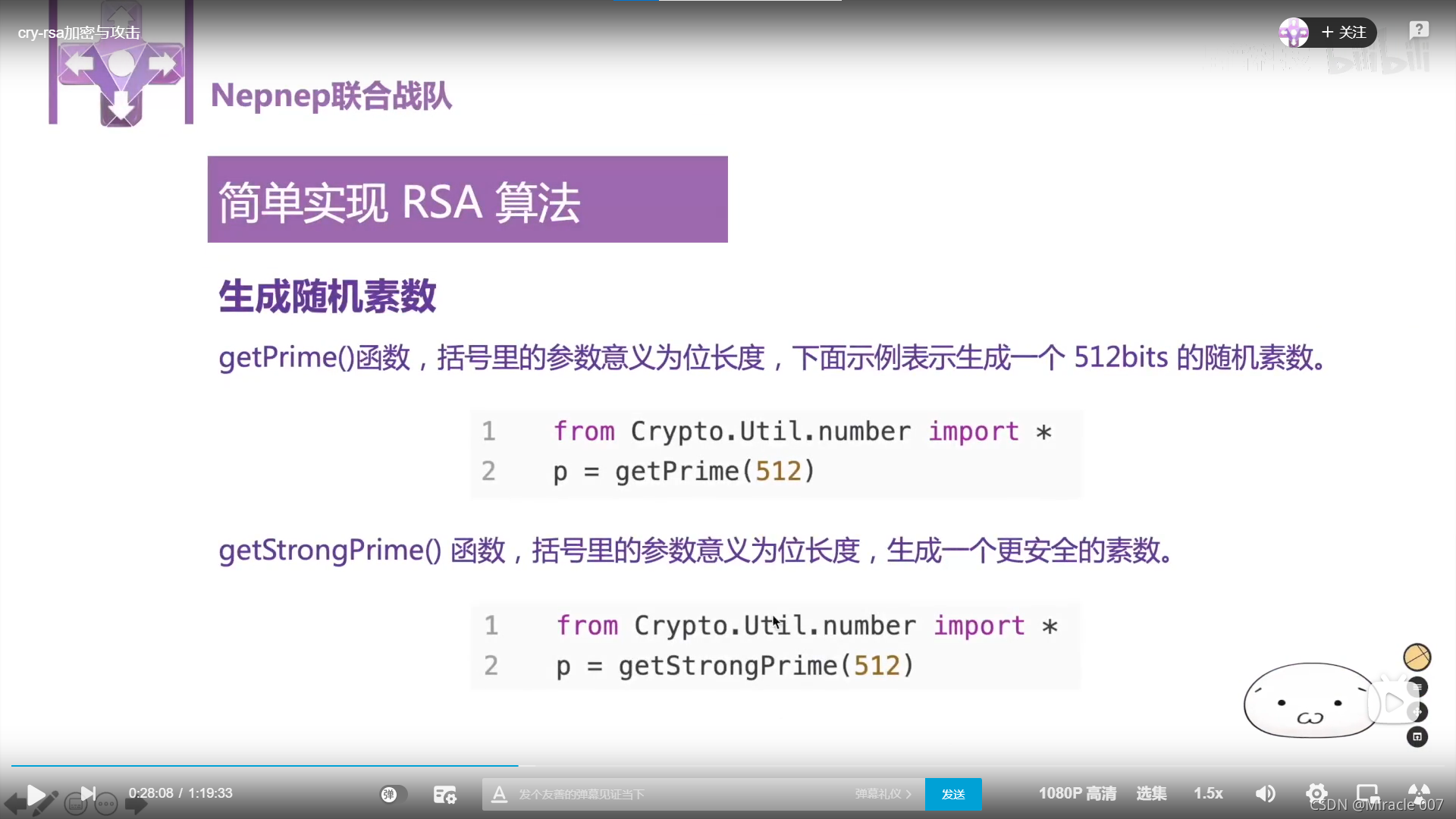
………………
RAS相关的攻击算法
1.分解素因数攻击

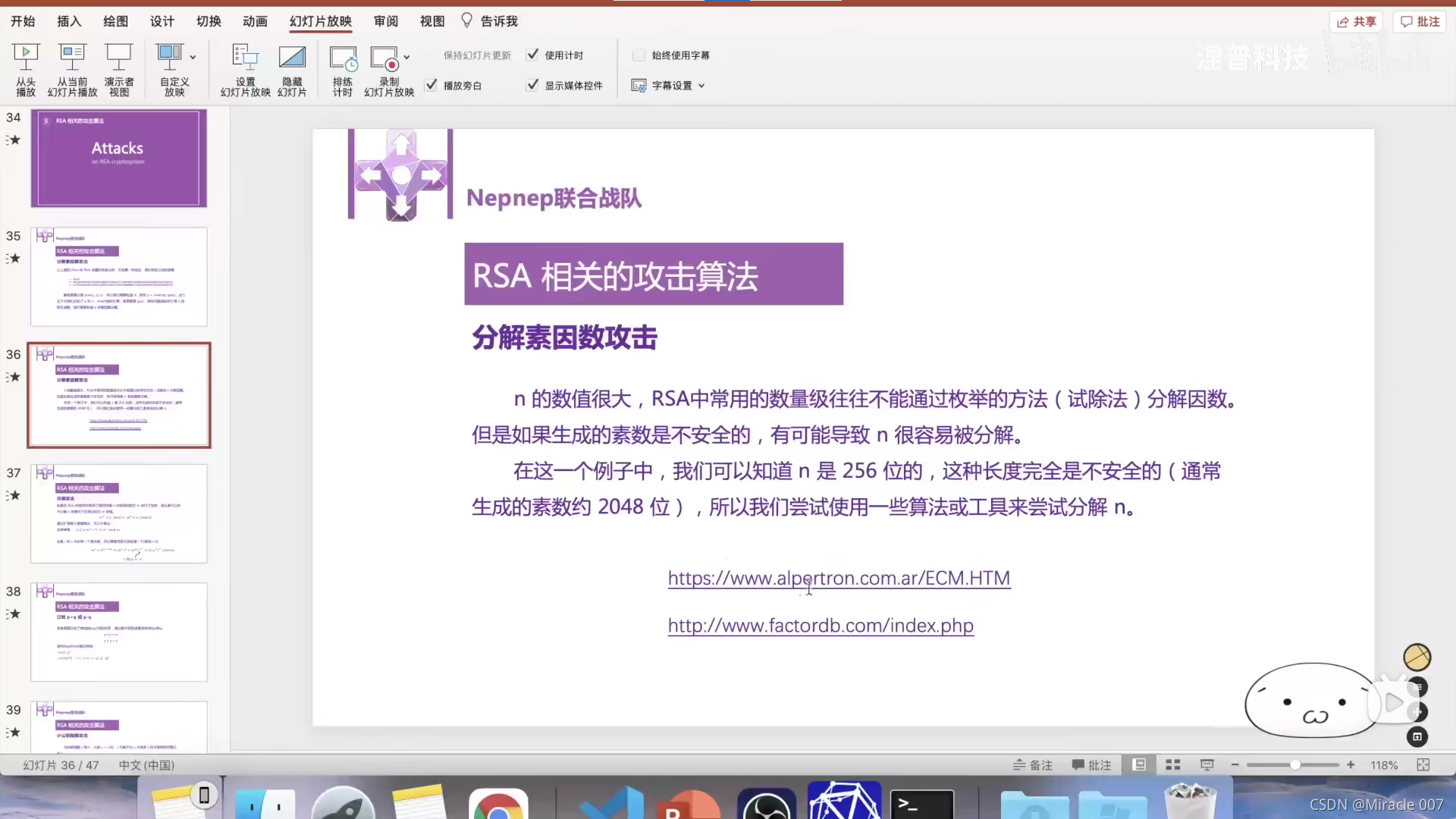
第一个链接:使用椭圆曲线分解算法
第二个链接:数据库查询
并不是所有的大数p,q都是安全的。
当p、q挨得很近的时候以及当p-1、q-1或者p+1、q+1是平滑数的时候(平滑数:p、q分解后最大的素因数比较小
或者比赛出现过的n。
2.共模攻击
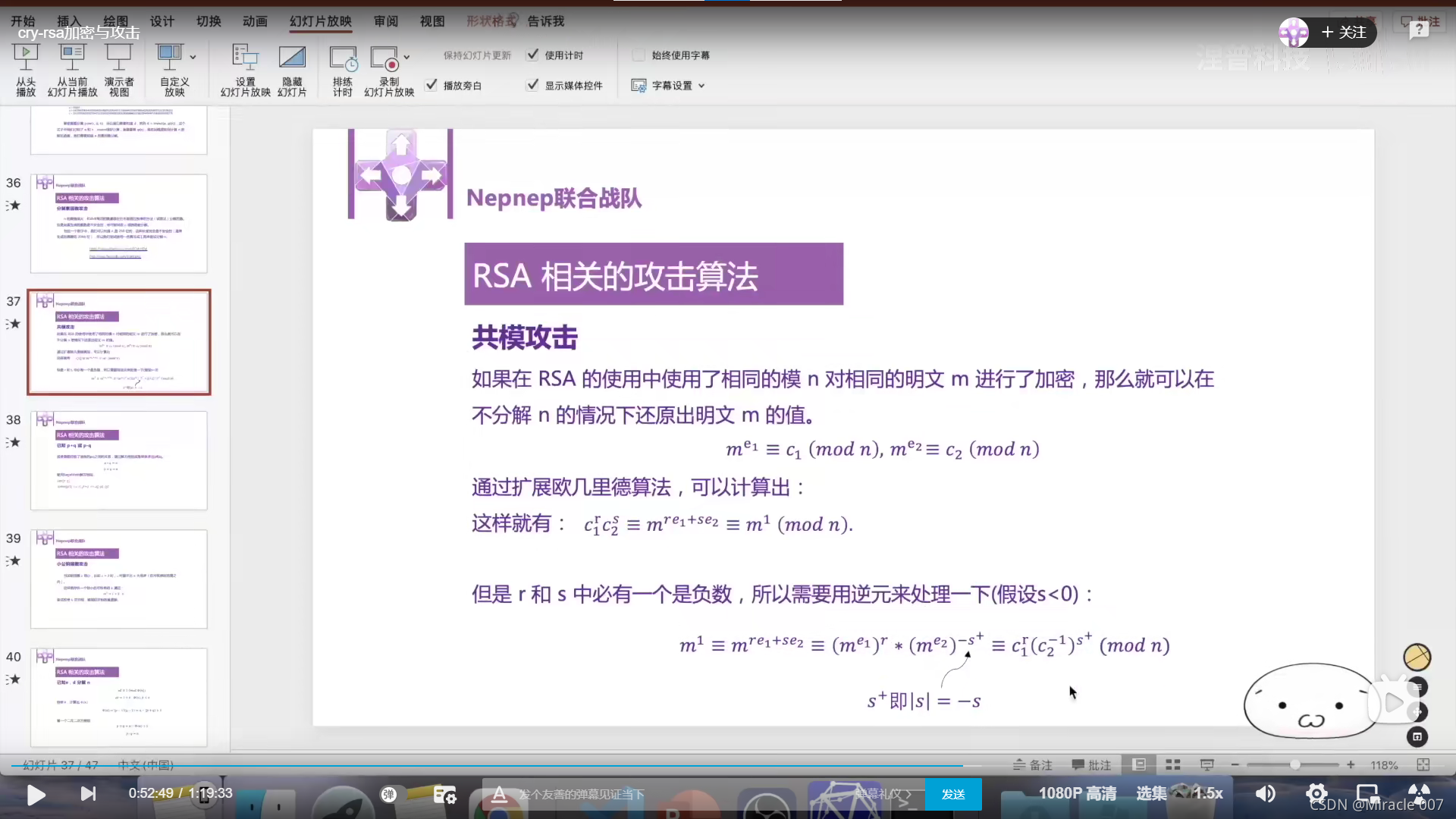
扩展欧几里得算法里,整数r和整数s是自己补上去的。这个式子不太懂,回头自己再看看。
因为e1和e2都是正整数所以r和s之中必然有一个负数,不然不可能得到1。
公钥加密只有私钥才能解密,私钥加密只有公钥才能解密,e和d是对等的,但是实际应用中私钥还会包含p和q。
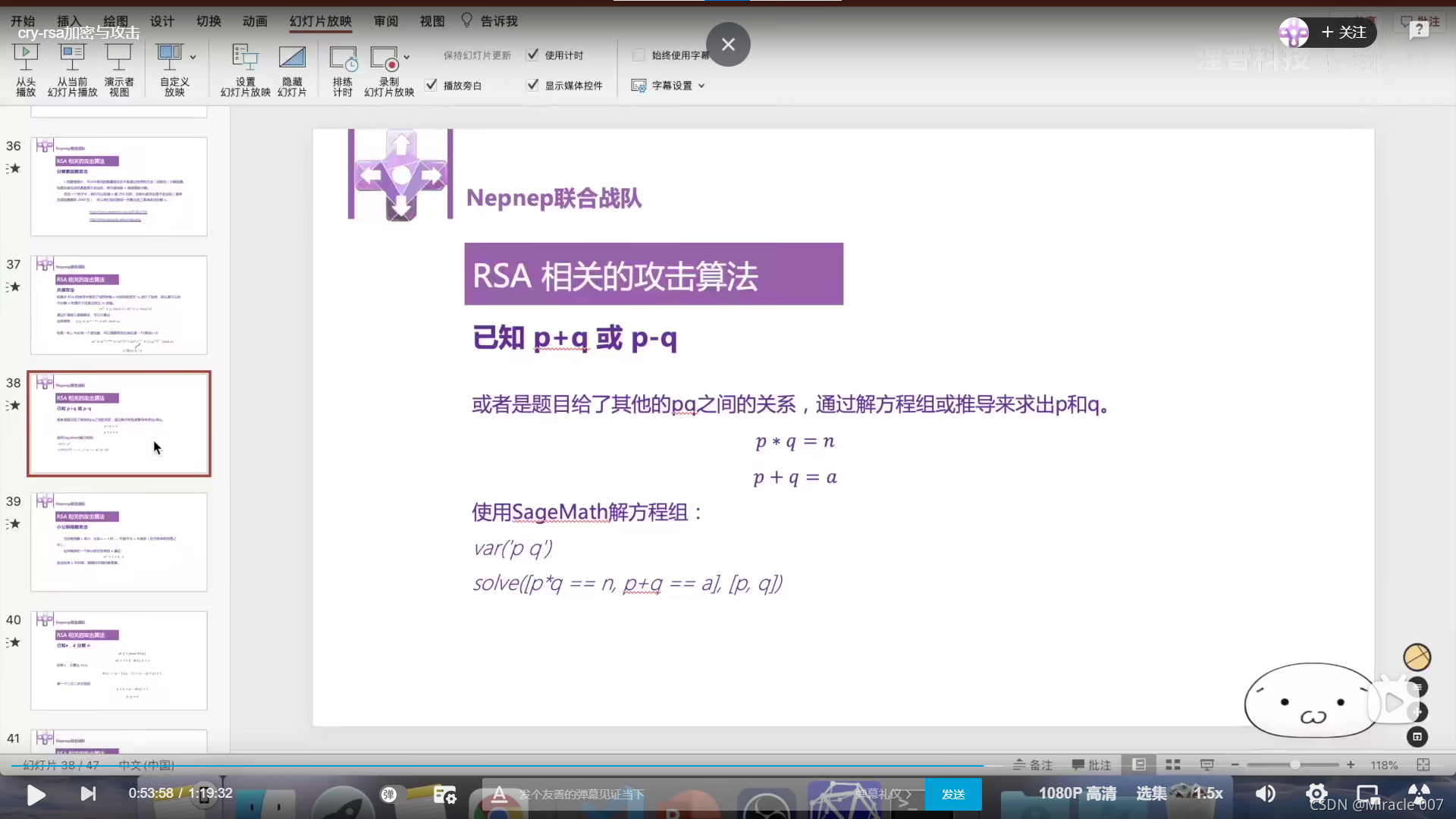
或者用二分法逼近求值
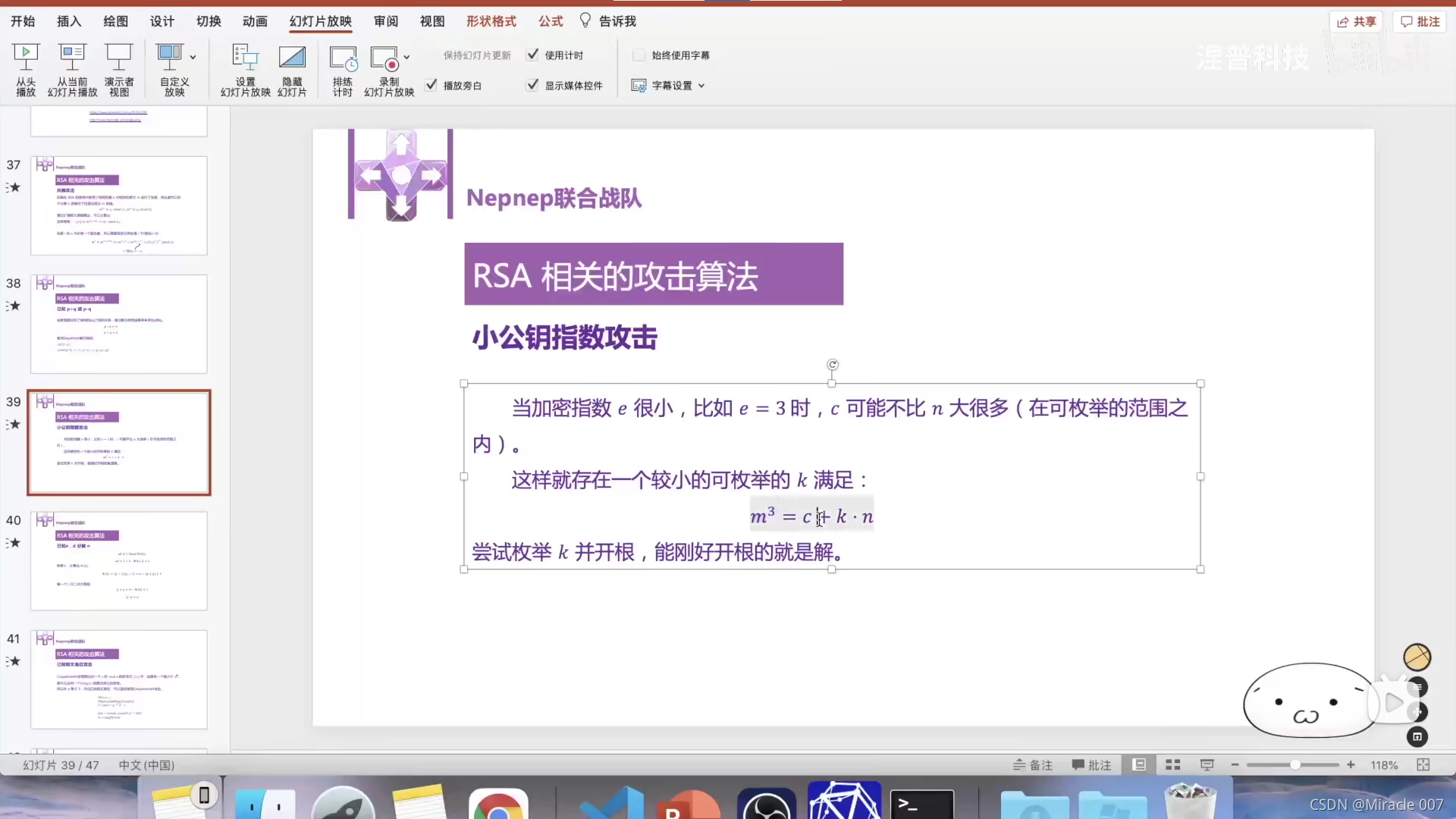
3.小公钥指数攻击
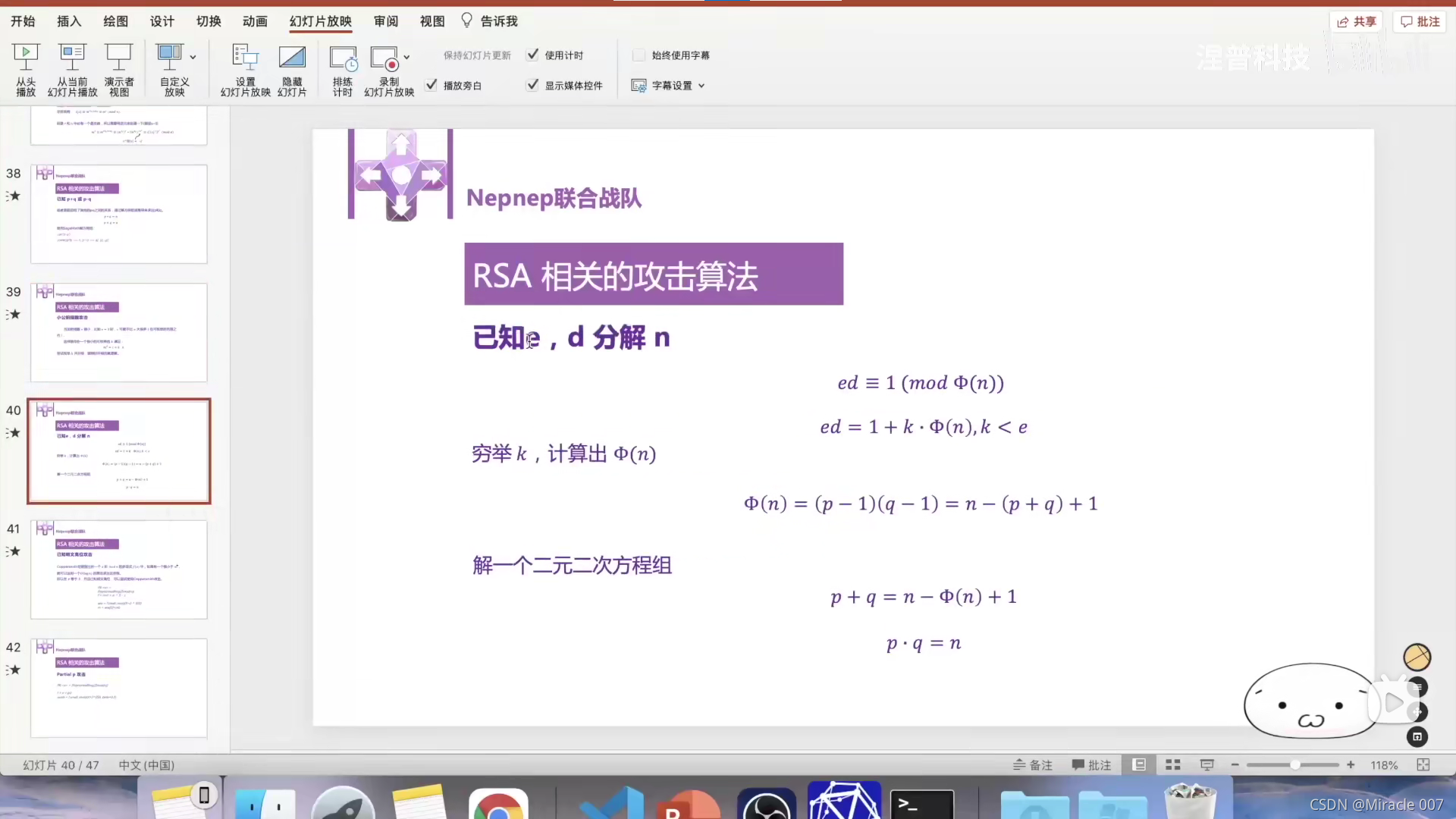
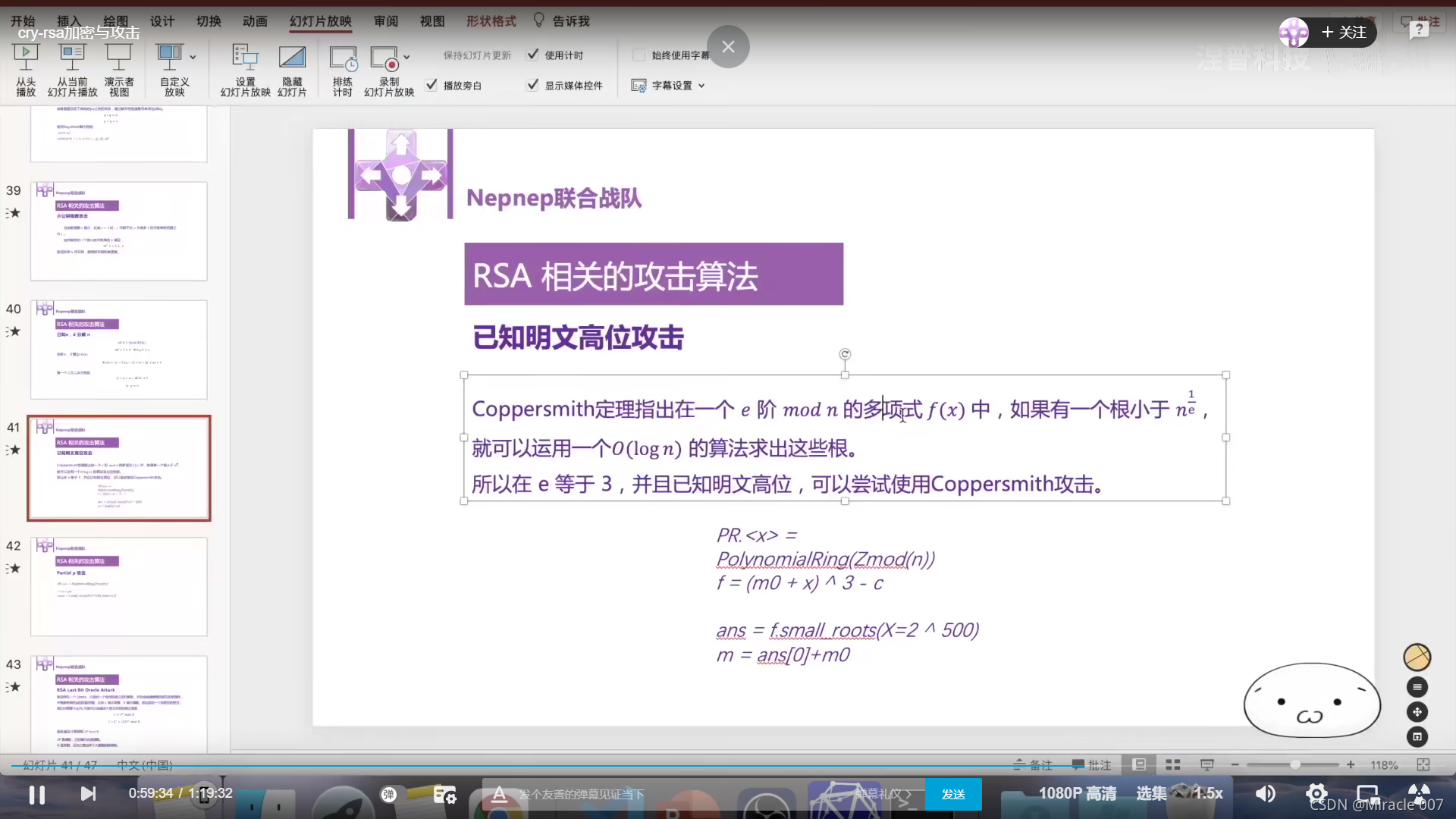
4.已知明文高位攻击
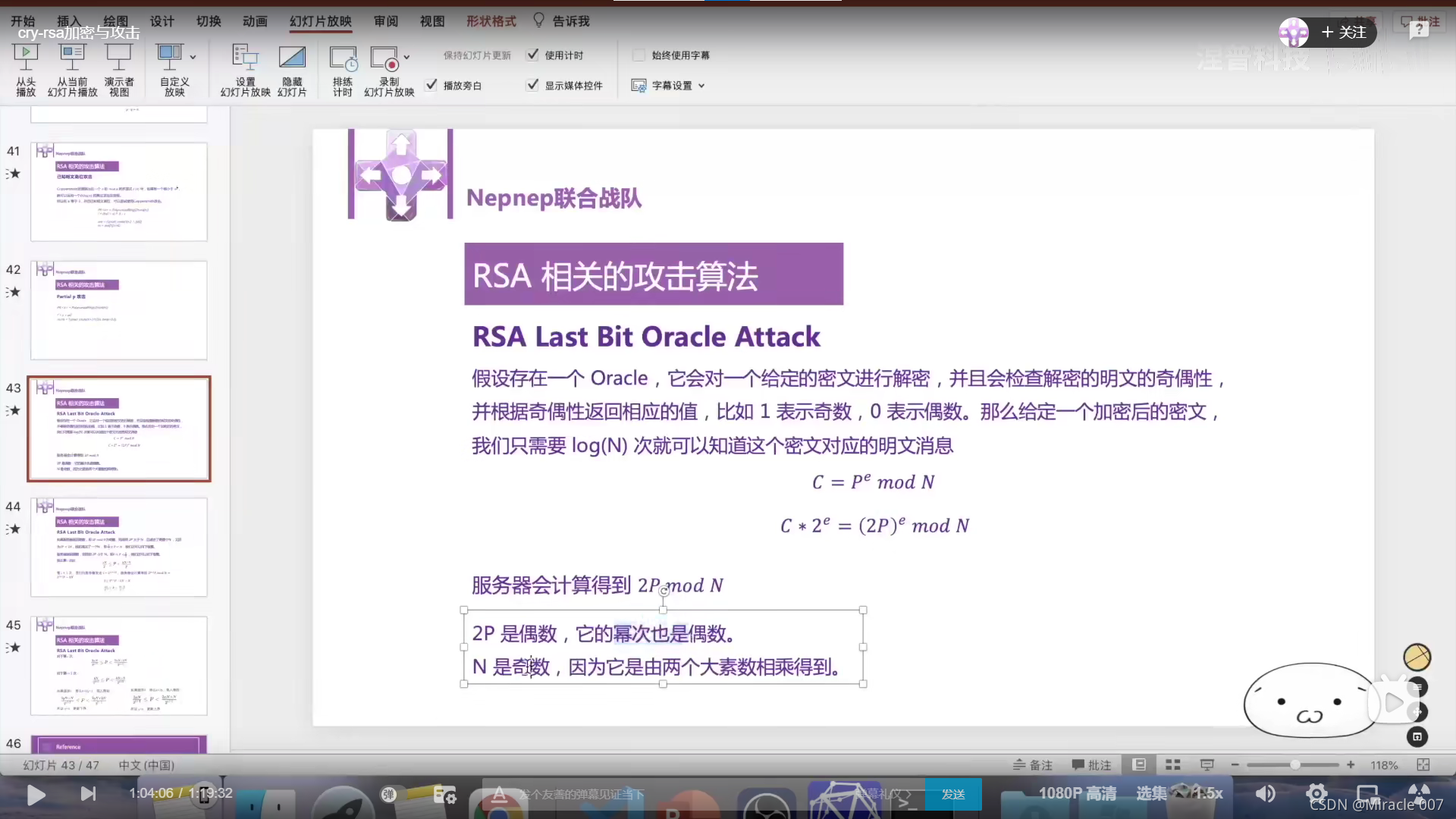
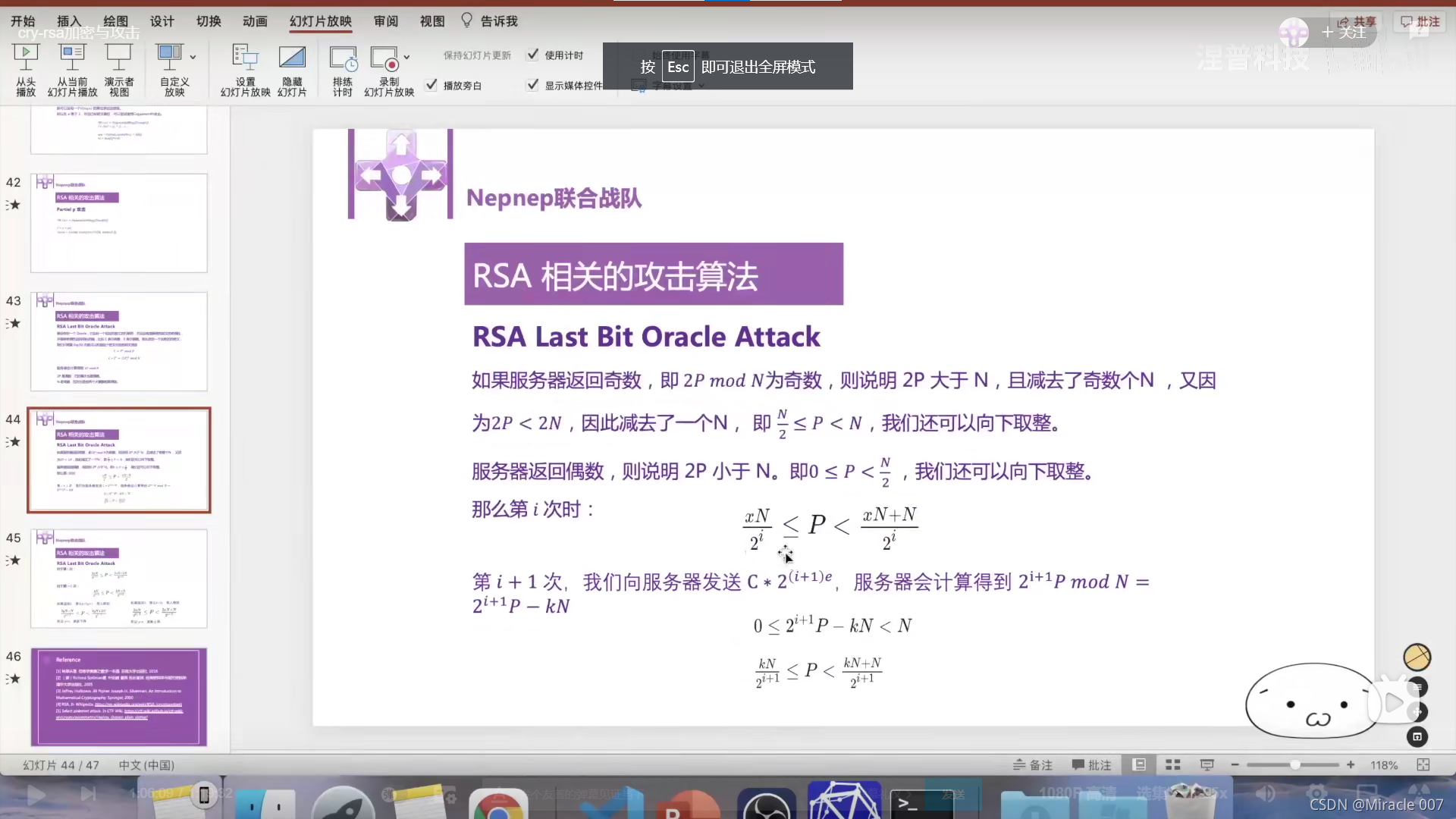
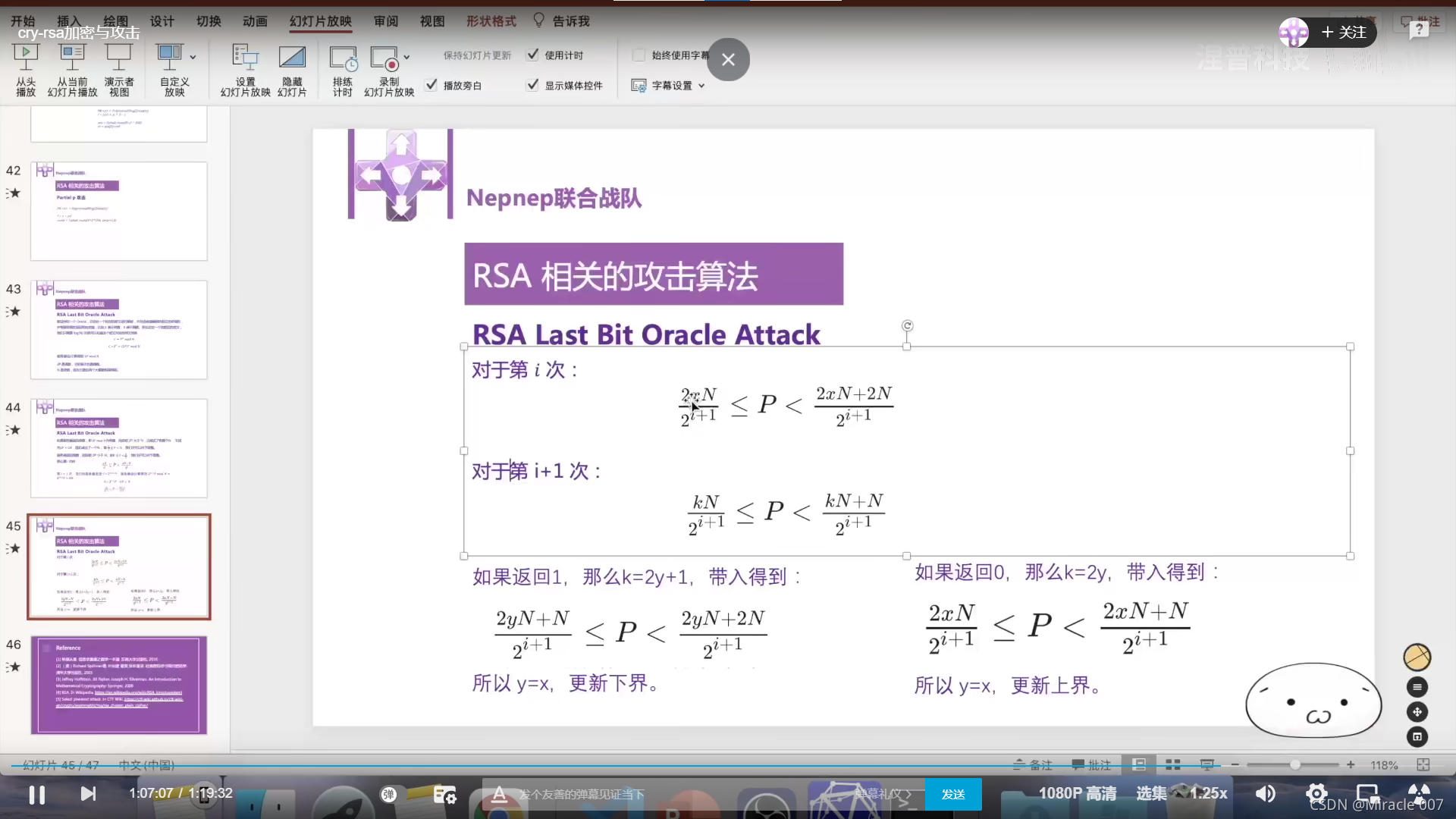
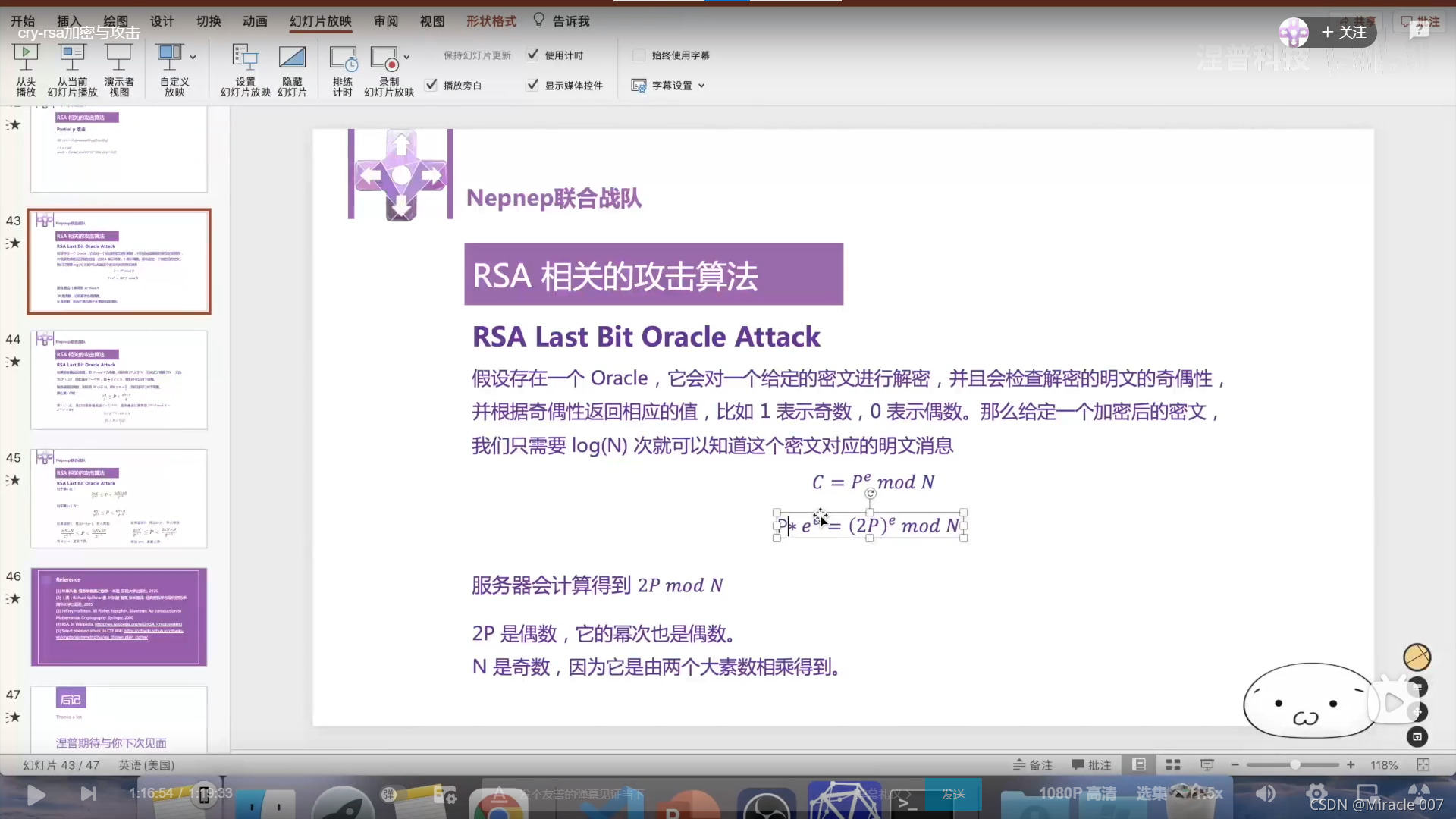
5.RSA Last Bit Oracle Attack 最低有效位攻击