题目
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
思路
题目中给出二叉树的根节点,要求二叉树的最大深度,很显然,二叉树只有左右两个方向,每一层代表深度加1,左右方向延伸的最大层数,就是二叉树的最大深度
那如何找到左右方向的最大深度呢,我们肯定需要取左右的较大值,并且进行递归遍历,从根节点开始,访问左右子节点,然后分别把左右子节点当成根节点,再访问相应的左右子节点
但是这时候,我们该怎么记录下来最大深度呢?
1.我们可以在进行递归的时候,每访问到下一层,就+1,最后返回记录的最大值
2.我们可以自底向上,左右子节点递归的返回到根节点
这里我们选择第二种做法,下面是我根据示例画出来的自底向上的图
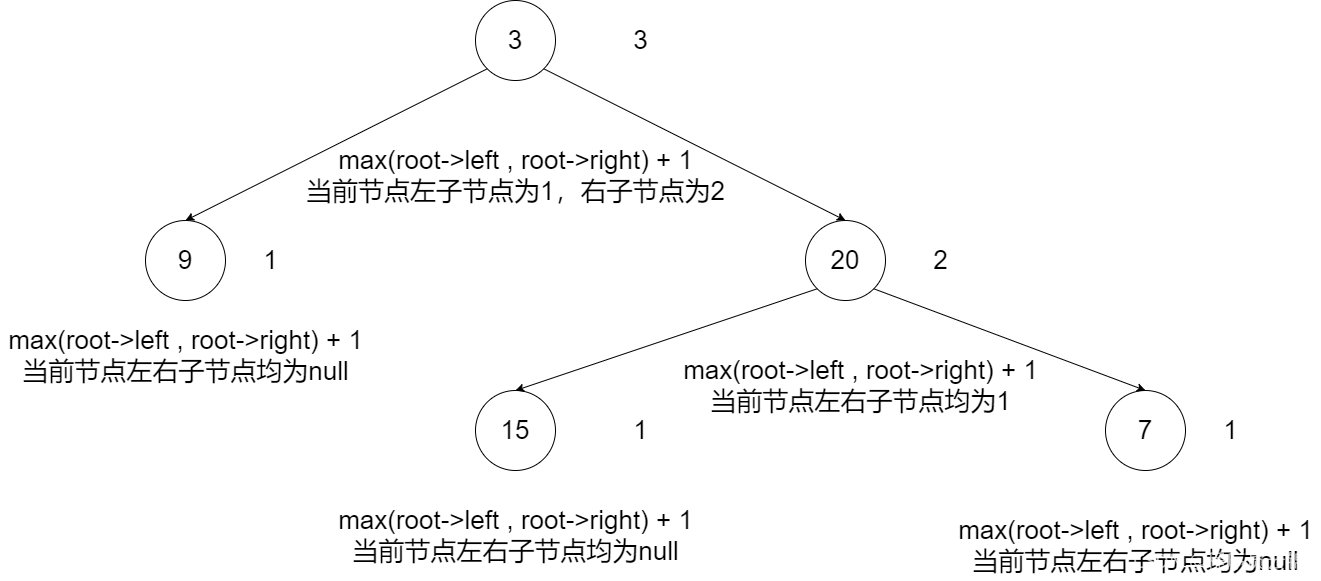
下面我们进入代码
代码
travel函数用于实现自底向上返回最大深度
进入travel函数中,首先判断节点是否为空,如果为空直接返回0,因为一个空节点是没有高度的
int travel(TreeNode* root) {
if(!root) {
return 0;
}
确定节点不为空之后,直接递归访问节点的左右子节点,并且取左右子节点的最大值后+1,这个+1是因为当前节点已经不为空了,所以需要加上当前节点的高度1
int travel(TreeNode* root) {
if(!root) {
return 0;
}
return max(travel(root -> left), travel(root -> right)) + 1;
}
至于主函数中,因为travel函数的值已经是二叉树的最大深度了,所以直接返回travel函数就行了,要记得把主函数中的root根节点参数传入travel函数
class Solution {
public:
int maxDepth(TreeNode* root) {
return travel(root);
}
};
最后把代码整合一下
完整代码:
class Solution {
public:
int travel(TreeNode* root) {
if(!root) {
return 0;
}
return max(travel(root -> left), travel(root -> right)) + 1;
}
int maxDepth(TreeNode* root) {
return travel(root);
}
};