目录
一、移除相同值的链表节点


思路:我们要删除所有为val的节点,就要先判断头节点是否为空,如果为空则直接返回空; 如果不为空,我们就定义两个节点,一个prev指向head节点,另一个cur指向head的下一个节点。当cur不为空时进行循环,如果cur的值等于要删除的val值,则让prev指向cur的下一个节点,cur再往后移一个节点;反之如果不等于的话,直接prev指向cur节点,再让cur节点往后移一个(先后顺序一定不能弄反),最后返回头结点即可,好了,这道题就这么...你是不是以为做到这步就结束了?too young too simple!
易错点:链表的题很多时候就是考察特殊情况,考你的细心程度。我们从定义cur到cur开始往后走的时候,自始至终都没有判断头结点是否也为val,因此我们最后判断一下头结点的值,这样再返回头结点,就大功告成了。
class Solution {
public ListNode removeElements(ListNode head, int val) {
if(head == null) return null;
ListNode prev = head;
ListNode cur = head.next;
while (cur != null) {
if(cur.val == val) {
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;
cur = cur.next;
}
}
//最后处理头
if(head.val == val) {
head = head.next;
}
return head;
}
}

二、反转一个单链表
给你头节点,请你反转链表,并返回反转后的链表。【OJ链接——反转链表】
 ?
?
思路:当头为空时,返回空;当不为空时,注意——这题要定义三个节点,一个cur,指向 head,代表从头节点开始遍历;一个prev,最开始为null,之后进入循环成为cur的前一个节点;一个curNext,指向cur的下一个节点。(有同学可能会不明白为什么这题要多定义一个curNext,因为这题是反转链表,当cur指向prev后,cur节点就与后面的节点的联系就彻底断了,只有先用curNext指向了cur的下一个节点,才能把后续节点全都反转)
易错点:cur是从head开始,而prev是从null开始,如果也像之前一样cur从head.next 并且 prev从head开始遍历的话,那么最开始的节点的next没有被置为空,而是保持指向后一个节点,这样链表就出问题了,因此要注意这点。
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null) return null;
ListNode cur=head;
ListNode prev=null;
while (cur!=null){
ListNode curNext=cur.next;
cur.next=prev;
prev=cur;
cur=curNext;
}
return prev;
}
}? ?
?
三、返回链表中间节点
(要求只能遍历单链表一遍)
 ?
?
思路:做这题我们要引入两个“指针”——fast 指针和slow 指针?。顾名思义,fast指针比slow走得更快。我们每次都使 slow 走一步,fast 走两步。这样下来,每次到最后 fast 等于?null 或者 fast.next 等于 null 时,slow所在的位置就刚好是我们要求的位置。(这是什么原理呢!是不是感觉很熟悉,路程公式S=V*T,当时间相同的情况下,fast 的速度是 slow 的两倍,那么最后 fast 的路程走的路程也是 slow 的两倍,当 fast 走完全程,slow 就刚好走完路程的一半)
奇/偶个节点都适用(如下图所示,当偶数个节点时,fast 走完,slow 刚好落在第二个中间节点的位置上)
? ?
?
易错点:注意细节,while 里的 fast != null 的判断条件要放在?fast.next != null 的前面,不然当fast 为空时就会变成空指针引用了~
class Solution {
public ListNode middleNode(ListNode head) {
ListNode slow=head;
ListNode fast=head;
while (fast!=null && fast.next!=null){
slow=slow.next;
fast=fast.next.next;
}
return slow;
}
}
 ?
?
?四、输出倒数第k个节点
输入一个链表,输出该链表中倒数第k个结点。【OJ链接—输出倒数第k个节点】
(要求只能遍历单链表一遍)
 ?
?
思路:本题同样要用到两个节点—— fast 与 slow,我们先来思考一个问题:倒数第k个节点到倒数第一个节点之间差多少步?答案是显然的(k-1)步。那么试想,如果我们让 fast 先走 k-1 步,然后再 fast 与 slow 同步走,是不是当 fast 走到倒数第一个节点后,slow此时对应的就是倒数第k个节点呢?
接下来我们画图验证一下:

结果是显而易见的,无论是奇数个节点还是偶数个节点,按照“ fast 先走k-1步,然后与slow同步走”的方法,最后得出的结果都是正确的,验证了我们的想法。因此开始写代码实现:
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
if(k<=0||head==null){
return null;
}
ListNode fast=head;
ListNode slow=head;
for(int i=0;i<k-1;i++){
fast=fast.next;
if(fast==null) {
return null;
}
}
while(fast.next!=null){
slow=slow.next;
fast=fast.next;
}
return slow;
}
}易错点:
1、k<=0 明显是不合法的,相信大家都能想到,但是还有一种需要额外判断的情况——在fast先走k-1步时,必须在 fast 每走一步的时候判断一下fast是否为空。(假设总共有五个节点,我输入的 k 为6,那么我的fast要先走5步,而走完第5步就 fast 就为空了!所以这是不可能的情况。因此 fast 如果为空,则说明这个输入的k值一定不合法!所以返回空值)
2、很多情况下都会忘记判断头结点是否为空,时刻注意头结点是个良好的习惯。

五、合并两个有序链表
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。【OJ链接——合并两个有序链表】
?
?
?思路:本题我们要先定义一个傀儡节点newHead,然后再定义一个tmp指向newHead,让tmp遍历链表。首先,因为所给两个链表都为升序,我们先判断l1与l2的值谁小——如果l1更小,则让tmp的next指向l1(因为我们要组成一个升序的链表),然后再让l1自己往后走一个,tmp也往后走一个到新组成链表的节点上,再次进行判断——l1与l2的值谁小(反复如此),那么肯定有同学想问,那如果他们值相等呢?这种情况随便指向哪个子链表的节点都行。那终止循环的条件是什么呢?当有一个链表会先被遍历完,即l1或者l2有一个,会先出现null。此时我们就退出循环,这也恰恰说明了,另一个不为空的链表的节点的值都比这个已经遍历完的链表节点的值都大。所以再将tmp.next指向不为空的节点,这样一个新的升序链表就被我们串起来了。
?代码如下:
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode newHead=new ListNode();
ListNode tmp=newHead;
while(l1!=null && l2!=null){
if(l1.val<l2.val){
tmp.next=l1;
l1=l1.next;
tmp=tmp.next;
}
else{
tmp.next=l2;
l2=l2.next;
tmp=tmp.next;
}
}
if(l1!=null){
tmp.next=l1;
}else if(l2!=null){
tmp.next=l2;
}
return newHead.next;
}
}
六、链表分割
编写代码,以给定值x为基准将链表分割成两部分,所有小于x的结点排在大于或等于x的结点之前。?【OJ链接——链表分割】

?思路:我们可以将这个链表分割为两个链表,小于所给节点值x的放在前面的链表,大于节点值x的放在后面的链表,最后再将两个链表拼接起来。如下图所示:bs为前面链表的起始节点,be为尾节点;as为后面链表的起始节点,ae为后面链表的尾节点。

所以大致流程就是——我们先定义一个cur指向head,让cur代head遍历链表。如果cur.val小于所给x的值,则判断bs里面是否为空,如果为空,则让be和bs都指向cur即可;如果bs不为空,则表示前面已经有节点了,则让be.next指向cur,之后be再往后走一步;如果cur.val大于所给x的值,与上述类似,只不过是放入后面的链表,用as与ae表示。每次判断完后cur都要往后走一步,最后当cur为空时(最初的链表全遍历完了),循环结束。
乍一听,是不是很简单?这不是有手就...NO NO NO,这题还有一些特殊情况,全是坑,一踩一个准。
易错点:
我们先来思考两个问题:
1、是所有数据都小于x吗?
2、原来链表的最后一个节点一定大于x吗?
接下来我们分析一下:
1、当后面链表为空时:(比如下图,给的值为999,谁也没我的值大),此时用be.next=as来连接,没问题。
2、当前面链表为空时:我们说到,最后要把be.next与as连起来,但是你有没有想过,前面链表为空呢(就比如下面这个图,我给的x值为1,压根没有比x小的值了呀,那前面的链表为空,执行起来不就空指针异常了吗)此时,我们需要在这条语句前判断一下bs是否为空,如果为空的话,返回as即可。(为什么返回as呢?因为要返回新的头结点,as为空,就刚好两个链表都为空,返回空即可;不为空,也要返回新的头结点as)
3、你以为这就结束了吗?这点是最容易被忽略的!当原链表最后一个节点的值小于x时,应该被放入前面的链表,而非后面!因此,造成了最后这个新的链表的最后一个节点的值不为空的情况!此时链表就没有尾节点了,因此,我们要手动将最后一个节点的值置为null。
至此,易错点也分析清楚了,我们就可以上手写代码了。
?文字太抽象,画个图更好理解,假设所给值为10,则有如下连接:
?
代码如下:
public class Partition {
public ListNode partition(ListNode pHead, int x) {
// write code here
ListNode bs = null;
ListNode be = null;
ListNode as = null;
ListNode ae = null;
ListNode cur = pHead;
while (cur != null) {
if(cur.val < x) {
//1、第一次
if(bs == null) {
bs = cur;
be = cur;
}else {
//2、不是第一次
be.next = cur;
be = be.next;
}
}else {
if(as == null) {
as = cur;
ae = cur;
}else {
//2、不是第一次
ae.next = cur;
ae = ae.next;
}
}
cur = cur.next;
}
//预防第一个段为空
if(bs == null) {
return as;
}
be.next = as;
//预防第2个段当中的数据,最后一个节点不是空的
if(as != null) {
ae.next = null;
}
return bs;
}
}
七、删除链表中重复的节点
在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。【OJ链接——删除链表中重复节点】


由题干,我们可得出两条重要信息:
1、重复的元素,不止一个。2、重复的元素,都是紧挨在一起的。
思路:因为涉及到删除元素,所以我们必须知道它的前一个节点,因此我们定义一个傀儡节点newHead,然后tmp指向newHead,让tmp往后走;然后让cur指向该链表的头结点head,让cur去走,tmp用来标记cur前面一个节点。此时我们先判断cur.val是否与cur.next.val相等,如果相等的话,则让cur进循环,往后走一个,当不等于时,出循环,再让cur往后走一个(为什么呢?因为你和后一个值相等时进循环,往后走一个说明cur所在的这个节点值还是重复的值,你要删除还得再往后走一个);反之如果值不相等的话,就让tmp.next指向cur,然后tmp与cur各往后走一步,最后返回新的头结点newHead.next。
易错点:还是一样,这题有很多容易出错的地方~相信大家思路上都没什么太大问题,一般都是细节上比较容易出错。?
1、用 cur.val==cur.next.val 作为判断时,我们应该让 cur.next 不能为空,就比如,只有一个节点的时候,cur.next就是空,那就直接空指针异常了,因此记得在使用时加上限制条件。
2、假如后面几个元素都是重复的情况下,此时走完之后 tmp.next 一定是不为空的,所以我们需要将它手动置为空。
了解之后,我们就可以着手写代码了。
?图示如下:
?
?代码如下:
public class Solution {
public ListNode deleteDuplication(ListNode head) {
ListNode newHead=new ListNode(-1);
ListNode cur=head;
ListNode tmp=newHead;
while(cur!=null){
if(cur.next!=null&&cur.val==cur.next.val){
while(cur.next!=null&&cur.val==cur.next.val){
cur=cur.next;
}
cur=cur.next;
}else{
tmp.next=cur;
cur=cur.next;
tmp=tmp.next;
}
}
tmp.next=null;
return newHead.next;
}
}
八、链表的回文结构
对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。【OJ链接——链表的回文结构】

思路:本题要寻找链表的回文结构,是一道经典面试题(据说字节出过此题哦),话不多说,我们来分析一下这道题。首先,回文结构意为结构相同、方向相反的序列。本题我们要判断一个结构是否为回文序列。那么我们分为几步:1、找到该链表的中间节点。2、从中间节点开始往后逆置链表。3、反转之后让两个指针朝中间走判断是否为回文序列。
具体过程:
大致的过程知道后,我们具体该如何实现呢?首先,找到链表的中间节点,这个方法我们在之前的题已经说过了,现在再复习一下——用 slow 指针与 fast 指针,slow一步 fast两步同时走,fast或fast.next为空时,slow所在节点即为中间节点。
那么找到了中间节点后,从中间节点往后逆置该如何实现呢?此时因为涉及到逆置,我们必须要知道逆置的节点和逆置的前一个节点与后一个节点。此时我们定义一个cur指向slow的下一个节点,然后当cur不为空时,进入循环,先定义一个curNext指向cur的下一个节点(因为当cur逆置后,就找不到后一个节点了,所以必须提前标记),再让cur.next指向slow,这样就成功逆置了,之后再让slow指向cur,cur指向curNext。这样当cur为空时退出循环,slow所在的节点就为该链表的最后一个节点。(因为slow一直为cur的前一个节点,当cur为空时slow就是最后一个节点了)
当我们逆置结束后,最后如何判断是否为回文序列呢?这就要分两种情况了——当链表的节点数量为奇数时,让slow与head(头结点)同时走,在他们相遇时,值一直相等则为true,否则为false;当链表的节点数量为偶数时,让slow与head同时走,不仅要在每一步的时候判断他们的值是否相等,还要判断 head.next是否等于slow (因为偶数节点不用走到相遇,最后的相遇即为相邻)
最后注意一下,当链表为空时,也属于回文结构。?
画个大概的图:?

?代码如下:
public class PalindromeList {
public boolean chkPalindrome(ListNode head) {
// write code here
ListNode slow=head;
ListNode fast=head;
if(head==null){
return true;
}
while(fast!=null&&fast.next!=null){
fast=fast.next.next;
slow=slow.next;
}
ListNode cur=slow.next;
while(cur!=null){
ListNode curNext=cur.next;
cur.next=slow;
slow=cur;
cur=curNext;
}
while(head!=slow){
if(head.val!=slow.val){
return false;
}
if(head.next==slow){
return true;
}
head=head.next;
slow=slow.next;
}
return true;
}
}
九、相交链表
输入两个链表,找出它们的第一个公共结点。【OJ链接——相交链表】?

思路:我们先想一个问题,两个链表如果长度不同,我们要如何走才能让两个节点从最开始走直到相遇?我们可以分别定义两个引用遍历两个链表获取各自长度,再进行相减得出它们之间相差的步数。再让长的那个链表先走相差的步数,再让两个节点同时走,就能达到相遇的目的。
具体实现的时候可以先定义两个引用 pl 与 ps,pl 指向两个链表中更长的头结点,ps 指向长度更短的链表的头结点。(那你最开始不知道哪个长怎么办?其实可以任意指定一个,因为你最后还是要进行判断修正的)然后再遍历获取两个链表的长度,用你默认的更长的长度减短的长度。如果最后得出的长度小于0就说明你默认的是相反的,再进行调换,把长度修正即可。最后让更长的那个pl先走差值步,再进入循环同步走,当他们相遇时,退出循环,返回pl/ps即可。?
?来个图可能更好理解:

易错点:1、任意所给头节点为空,即返回空。(都为空哪来的公共结点)
2、当你用pl/ps遍历链表时,遍历完后pl/ps都为空。为了后续判断长度差值之后的遍历,需要手动将它们指向各自最开始的头结点。
代码如下:
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null||headB==null){
return null;
}
ListNode pl=headA;
ListNode ps=headB;
int lenA=0;
int lenB=0;
while(pl!=null){
lenA++;
pl=pl.next;
}
pl=headA;
while(ps!=null){
lenB++;
ps=ps.next;
}
ps=headB;
int len=lenA-lenB;
if(len<0){
pl=headB;
ps=headA;
len=lenB-lenA;
}
for(int i=0;i<len;i++){
pl=pl.next;
}
while(pl!=ps){
pl=pl.next;
ps=ps.next;
}
return pl;
}
}
十、判断链表是否有环
给定一个链表,判断链表中是否有环。【OJ链接——环形链表】
?
思路:这题是经典题了,我们先思考一下过程——首先定义两个快慢“指针”指向头结点,一个slow 一个fast,照样让fast两步,slow一步同时走,当fast且fast.next不为空时,进入循环,每走一步判断一下它们是否相遇了,相遇则链表有环,循环结束还没相遇,说明链表无环。

?
?本题代码比较简单,注意一下 while 里 fast 的判断必须得放在 fast.next 前面即可。
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast=head;
ListNode slow=head;
if(head==null){
return false;
}
while(fast!=null && fast.next!=null){
fast=fast.next.next;
slow=slow.next;
if(fast==slow){
return true;
}
}
return false;
}
}十一、找到环形链表的入环节点
给定一个链表,返回链表开始入环的第一个节点。如果链表无环,则返回?
null。【OJ链接——返回环形链表第一个节点】

?思路:本题要找循环链表的入环节点,有一个结论——如果有两个引用,一个从头开始,一个从相遇点(相遇点的求法为“快慢指针法”)开始,一人一步走,最后相遇的地方就是入环节点。
下面我们证明一下这个结论:
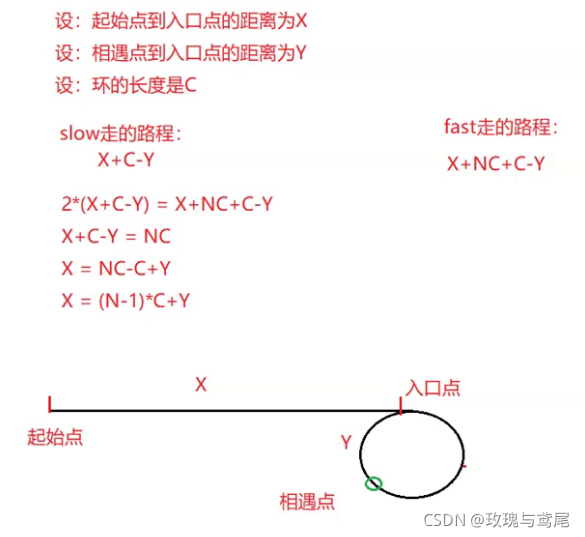
由上述推导可得,当N=1时,起始点到入口点的距离等于相遇点到入口点的距离;当N大于1的情况下,从相遇点走的那个引用走到入口点后又在环中绕了(N-1)圈,最终在入口点的位置与从头部走的引用相遇了。
证明完之后,就可以分析具体流程了:
1、我们先定义两个引用slow和fast,然后用快慢指针法,找到并记录它们在环中相遇的位置。
2、让slow指向起始点位置,fast指向相遇点的位置(此时当然也可调换位置,因为现在开始它们走的速度是相同的),然后一步一步走,每走完一步判断他们是否相遇,如果相遇,则返回该节点(由上述推导可得最后相遇点的地方就是入环节点)
?代码如下:
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow=head;
ListNode fast=head;
if(head==null||head.next==null){
return null;
}
while(fast!=null && fast.next!=null){
slow=slow.next;
fast=fast.next.next;
if(fast==slow){
ListNode meet=fast;
break;
}
}
if(fast!=slow){
return null;
}
slow=head;
while(slow!=fast){
slow=slow.next;
fast=fast.next;
}
return slow;
}
}易错点:当链表为空,或者链表只有一个节点的时候,都没有环,记得返回空值。

本文到此结束,如有不当之处,还望各位指出,希望能和大家一起共同进步!