目录
写在前面
笔者按去年实际考试内容,回忆并编写本博客。建议大家收藏,如对考试有帮助,记得回来丢个赞。如果对部分内容有疑问可以直接留言。
机考篇
大致内容
去年第一题、第二题为顺序表,第三题为排序,第四题主要考dfs。第五题为压轴题考了三叉霍夫曼树
数据结构期末机考大致有5道题,难度由浅入深,根据去年实际体验,大致人均AC2~3题。前三题的难度会相对比较简单,主要需要重点复习下顺序表,链表等线性结构,排序算法(选择,插入,冒泡…),哈希查找。第四题一般会相对难一些,需要重点复习一下图的dfs,bfs。最短路径的Dijkstra算法以及最小生成树Prim和Kruskal算法。最后一题会比较难,可能会遇到比较复杂的数据结构,机考过程中前四题全部AC后可以试一下。
例题
这部分的两道题大概是去年机考的第四第五题(前面题记不清了),凭着回忆把题目重新写了下,又做了一遍,自己敲了标程。
无向图求割点
按输入顺序输出无向图的所有割点。(割点:在一个无向图中,如果删除某个顶点以及与该顶点相关联的所有边后,图的连通分量增多,就称这个点为割点。)
输入
第一行为测试数据数。对于每组测试数据,第一个整数
n
n
n表示该无向图的大小。接下来
n
n
n个字符串为每个顶点的名称。接下来输入一个
n
?
n
n*n
n?n的方阵作为无向图,0表示两个顶点之间不存在边,1表示两个顶点之间存在边。
输出
输出各个割点的名称。每组测试数据的输出占一行。如果没有割点,则输出No!
样例输入
4
8
0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0
0 0 0 1 1 0 0 0
0 0 0 1 1 1 1 0
0 1 1 0 0 0 0 0
0 1 1 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 1 0 0 0 0 1
0 0 0 0 0 0 1 0
3
A B C
0 1 0
1 0 1
0 1 0
5
a b c d e
0 1 0 0 1
1 0 1 1 0
0 1 0 0 0
0 1 0 0 0
1 0 0 0 0
6
v1 v2 v3 v4 v5 v6
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
样例输出
2 6
B
a b
No!
参考代码
#include <iostream>
#include <vector>
using namespace std;
bool *isVisited;
int **matrix;
int n = 0;
//node:当前深搜点 cur:当前判断的割点
void dfs(int node, int cur) {
isVisited[node] = true;
for (int i = 0; i < n; i++) {
if ((!isVisited[i]) && i != cur && node != cur && (matrix[node][i] || matrix[i][node])) {
dfs(i, cur);
}
}
}
int main() {
int t;
cin >> t;
while (t--) {
cin >> n;
vector<string> vertex;
vector<string> res;
isVisited = new bool[n];
matrix = new int *[n];
for (int i = 0; i < n; i++) {
string temp;
cin >> temp;
vertex.push_back(temp);
matrix[i] = new int[n];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
int cc = 0;
for (int i = 0; i < n; i++) {
if (!isVisited[i]) {
cc++;
dfs(i, -1);
}
}
for (int i = 0; i < n; i++) {
int temp = 0;
for (int ii = 0; ii < n; ii++) {
isVisited[ii] = false;
}
for (int j = 0; j < n; j++) {
if (!isVisited[j]) {
temp++;
dfs(j, i);
}
}
if (temp > cc + 1) {
res.push_back(vertex[i]);
}
}
if (res.empty()) {
cout << "No!" << endl;
} else {
for (int i = 0; i < res.size(); i++) {
cout << res[i] << " ";
}
cout << endl;
}
}
return 0;
}
三叉霍夫曼
给定n个权值,根据这些权值构造三叉霍夫曼树,并进行三叉霍夫曼编码。
输入
第一行输入
t
t
t,表示有
t
个
t个
t个测试实例
第二行先输入
n
n
n,表示第1个实例有
n
n
n个权值,接着输入
n
n
n个权值,权值全是小于1万的正整数
依此类推
输出:
逐行输出每个权值对应的编码,格式如下:权值-编码
即每行先输出1个权值,再输出一个短划线,再输出对应编码,接着下一行输出下一个权值和编码。
以此类推
样例输入
2
8
1 5 3 4 9 2 6 10
10
1 5 9 6 3 4 7 8 11 12
样例输出
1-100
5-01
3-102
4-00
9-11
2-101
6-02
10-12
1-010
5-120
9-02
6-121
3-011
4-012
7-122
8-00
11-10
12-11
样例代码
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
struct Node {
int value;
int father = -1;
int son[3];
string code;
Node(int value, int father) {
this->value = value;
this->father = father;
for (int i = 0; i < 3; i++) {
this->son[i] = -1;
}
}
};
bool cmp(const Node &a, const Node &b) {
return (a.father == -1 ? a.value : (9999 + a.value)) < (b.father == -1 ? b.value : (9999 + b.value));
}
int getNode(int num, vector<Node> nodeList) {
for (int i = 0; i < nodeList.size(); i++) {
if (nodeList[i].value == num && nodeList[i].father == -1) {
return i;
}
}
return -1;
}
void dfs(int index, vector<Node> &nodeList) {
if (index == -1) {
return;
}
for (int i = 0; i < 3; i++) {
if (nodeList[index].son[i] == -1) {
continue;
}
nodeList[nodeList[index].son[i]].code += (nodeList[index].code + to_string(i));
dfs(nodeList[index].son[i], nodeList);
}
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
vector<Node> nodeList;
for (int i = 0; i < n; i++) {
int temp;
cin >> temp;
nodeList.push_back(Node(temp, -1));
}
while (true) {
vector<Node> temp(nodeList);
sort(temp.begin(), temp.end(), cmp);
if (temp[2].father == -1) {
nodeList.push_back(Node(0, -1));
for (int i = 0; i < 3; i++) {
nodeList[nodeList.size() - 1].value += temp[i].value;
nodeList[nodeList.size() - 1].son[i] = getNode(temp[i].value, nodeList);
nodeList[getNode(temp[i].value, nodeList)].father = nodeList.size() - 1;
}
continue;
} else if (temp[1].father == -1) {
nodeList.push_back(Node(0, -1));
for (int i = 0; i < 2; i++) {
nodeList[nodeList.size() - 1].value += temp[i].value;
nodeList[nodeList.size() - 1].son[i] = getNode(temp[i].value, nodeList);
nodeList[getNode(temp[i].value, nodeList)].father = nodeList.size() - 1;
}
break;
} else {
break;
}
}
dfs(nodeList.size() - 1, nodeList);
for (int i = 0; i < n; i++) {
cout << nodeList[i].value << "-" << nodeList[i].code << endl;
}
}
return 0;
}
笔试篇
笔试篇按上课讲课顺序,以章节为单位进行组织
Chapter 1
- 逻辑结构四种基本形式:集合结构,线性结构,树状结构,图状结构
- 数据结构是二元组(数据对象,对象中所有数据成员之间关系的有限集合)
- 存储结构(又叫物理结构)——顺式,链式(索引,散列)
- 算法:有穷性,确定性,可行性,有输入&输出
- 大 O O O标记法=>时间复杂度&空间复杂度
Chapter 2
- 顺序表
- 基本操作:插入,删除,合并
- 优点:可以随机存取,元素地址可用简单公式表示
- 缺点:插入或删除时要移动大量元素,占用连续地址空间
- 链表
- 单链表
- 每个节点只有一个指针域
- 指针是元素之间逻辑关系的映像
- 地址不连续
- 插入删除方便,查找需要遍历
- 插入:头插,尾插(头插需要逆序输入)
- 循环链表
- 每个节点有两个指针,前驱prior,后继next
- 插入删除需要改变两个方向的指针
- 链表存储密度小于1
- 一般顺序表空间为静态分配,链表动态分配
- 单链表
Chapter 3
- 栈:Stack
- 后进先出 LIFO
- 顺序栈
- top=base 空栈
- base=NULL 栈不存在
- 插入元素/删除元素:top++/top–
- top-base=stacksize 栈满
- 链栈
- 栈的应用:数制转换,括号匹配,行编辑程序,迷宫求解,表达式求解(逆波兰式)
- 队列:Queue
- 先进先出 FIFO
- rear队尾指针->头元素,front队头指针->队尾元素的下一个位置
- 单链队列:无队满问题,有队空问题
- 顺序队列:进队rear++,出队front++
- 循环队列:
- front=rear 队空
- (rear+1)%MAXSIZE=front (少用一个空间以区分空队)
- 插入:rear=(rear+1)%MAXSIZE
- 删除:front=(front+1)%MAXSIZE
- 队列长度:(rear-front+MAXSIZE)%MAXSIZE
Chapter 4
- 串
- 子串,真子串
- 块链存储,存储密度小于1
- 模式匹配
- 朴素算法:BF算法(Brute Force)
- 主串指针重复回溯
- 最优时间复杂度 O ( n ) O(n) O(n)(n为模式串长,m为主串长)
- 最差时间复杂度 O ( n ? m ) O(n*m) O(n?m)
- KMP算法:主要思想是消除主串指针重复回溯
- next函数:只与模式串有关,与主串无关
- n e x t [ j ] = { 0 j = 1 max ? ( k ∣ 1 < k < j 且 ′ t 1 . . . t k ? 1 ′ = ′ t j ? k + 1 . . . t j ? 1 ′ ) 当 此 集 合 非 空 时 1 e l s e next[j]=\begin{cases} 0 & j=1 \\ \max(k|1<k<j 且't_1...t_{k-1}'='t_{j-k+1}...t_{j-1}') & 当此集合非空时 \\ 1 & else \end{cases} next[j]=??????0max(k∣1<k<j且′t1?...tk?1′?=′tj?k+1?...tj?1′?)1?j=1当此集合非空时else?
- KMP算法改进:nextval
- 时间复杂度 O ( n + m ) O(n+m) O(n+m)
- 朴素算法:BF算法(Brute Force)
| j j j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 模式串 | a | b | a | c | a | b | a | a | a | d |
| n e x t [ j ] next[j] next[j] | 0 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 2 | 2 |
| n e x t v a l [ j ] nextval[j] nextval[j] | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 4 | 2 | 2 |
Chapter 5
- 数组
- 行优先顺序,列优先顺序
- 地址计算
- 矩阵
- 矩阵压缩
- 对称矩阵
- 存储空间优化: n 2 ? > n ( n + 1 ) 2 n^2->\frac{n(n+1)}{2} n2?>2n(n+1)?
- k = { i ( i ? 1 ) 2 + j ? 1 i ≥ j j ( j ? 1 ) 2 + i ? 1 i < j k=\begin{cases} \frac{i(i-1)}{2}+j-1 & i\geq j \\ \frac{j(j-1)}{2}+i-1 & i< j \end{cases} k={2i(i?1)?+j?12j(j?1)?+i?1?i≥ji<j?
- 三角矩阵
- 稀疏矩阵:三元组存储 ( i , j , a i j ) (i,j,a_{ij}) (i,j,aij?)
- 对称矩阵
- 矩阵压缩
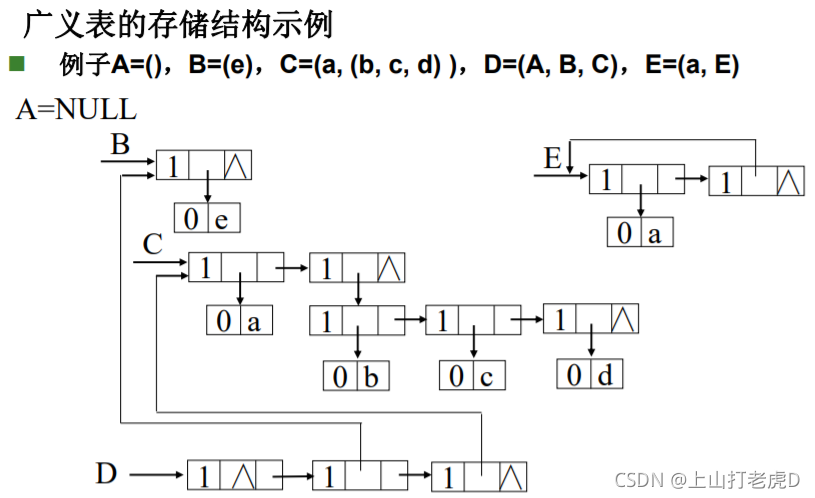
- 广义表:
a
1
a_1
a1?表头,
(
a
2
,
.
.
.
,
a
n
)
(a_2,...,a_n)
(a2?,...,an?)表尾
- 长度:元素个数
- 深度:嵌套深度(递归)
- 例1: A = ( ) A=() A=()长度为0,深度为1
- 例2: B = ( ( ) ) B=(()) B=(())长度为1,深度为2
- Head 取表头,Tail 取表尾
- 表节点tag=1,原子节点tag=0
Chapter 6
- 树
- 概念:节点,节点的度,树的度,叶子节点(终端节点),分支节点(非终端节点),孩子,兄弟,祖先,层次,深度(高度),有序树,无序树,森林
- 性质:树中节点数减一等于度数和
- 二叉树
- 性质:第 i i i层至多有 2 i ? 1 2^{i-1} 2i?1个节点,深度为 k k k的二叉树最多有 2 k ? 1 2^{k-1} 2k?1个节点。二叉树终端节点数等于二度节点数加一
- 完全二叉树:叶子节点只在最后两层,左子树深度等于右子树深度或大一
- 深度: ? log ? 2 n ? + 1 \lfloor\log_2{n}\rfloor+1 ?log2?n?+1
- 双亲: ? n 2 ? \lfloor\frac{n}{2}\rfloor ?2n??
- 左孩子: 2 ? i 2*i 2?i,右孩子: 2 ? i + 1 2*i+1 2?i+1
- 二叉树顺序存储:浪费空间
- 二叉链表
- 含有n节点的二叉链表有n+1个空指针域
- 二叉树遍历:非线性结构线性化
- DLR:先序遍历
- LDR:中序遍历
- LRD:后序遍历(根节点最后一个输出)
- 逆波兰式另一种解法:通过后序遍历形成后缀表达式
- 层次遍历:队列实现(出队一个节点,入队左右孩子)
- 先序非递归实现:栈存右孩子
- 线索二叉树
- 线索:指向前驱和后继的指针
- 线索链表
- 遍历线索树不需要栈
- 树与森林
- 双亲表示法:多重链表(空链域太多)
- 单链表
- 孩子兄弟表示法
- 左指针:孩子
- 右指针:兄弟
- 森林与树的转换
- 对森林的先序遍历:从左到右一次先序
- 对森林的中序遍历:从左到右依次后序
- 赫夫曼树(最优二叉树)
- 路径,路径长度,树的路径长度
- 节点的带权路径长度,树的带权路径长度
- 权值大离根近,权值小离根远
- 不存在1度节点
- 如果有n个叶子节点,则共有2n-1个节点
- 赫夫曼编码:不等长编码,目的是缩短编码长度
- 编码与解码
Chapter 7
- 图
-
无向图:邻接点,度,关联
-
无向完全图: 1 2 n ( n ? 1 ) \frac{1}{2}n(n-1) 21?n(n?1)条边
-
有向图:邻接点,入度,出度,关联
-
有向完全图: n ( n ? 1 ) n(n-1) n(n?1)条边
-
稀疏图,稠密图
-
连通,连通图,连通分量
-
强连通,强连通图,强连通分量
-
图的表示:邻接矩阵,邻接表(逆邻接表)
-
稠密图用邻接矩阵存储,稀疏图用邻接表存储
-
图的遍历:dfs,bfs
-
dfs:栈实现,先根遍历推广 邻接矩阵 O ( n 2 ) O(n^2) O(n2) 邻接表 O ( n + e ) O(n+e) O(n+e)
-
bfs:队列实现,数层次遍历 邻接矩阵 O ( n 2 ) O(n^2) O(n2) 邻接表 O ( n + e ) O(n+e) O(n+e)
-
连通分量
-
生成树(bfs生成树,dfs生成树)=》生成森林
-
最小生成树
- Prim算法:
- 选点思想:适用于稠密图
- O ( n 2 ) O(n^2) O(n2)
- Kruskal算法
- 选边思想:适用于稀疏图
- O ( e log ? e ) O(e\log e) O(eloge)
- Prim算法:
-
AOV网
- 关键路径:路径长度,关键活动
- 顶点对应事件,边对应活动
- 最早发生时间,最晚开始时间
- 最早开始时间,最晚开始时间,时间余量
- 最早:正向拓扑 最晚:反向拓扑

-
最短路径
- 迪杰斯特拉算法 O ( n 2 ) O(n^2) O(n2)
-
Chapter 9
-
查找表:静态查找表,动态查找表
-
关键字:主关键字(唯一),次关键字(不唯一)
-
静态表:顺序表,有序表(折半查找,插值查找),索引顺序表,斐波那契查找
-
动态表:二叉排序树,平衡二叉树,B树,散列表
-
评价标准:平均查找长度:ASL
-
顺序表与链表:遍历逐个找
- 优点:简单,适应面广
- 缺点:ASL比较大,数据多时查找效率很低
-
索引查找表:先根据索引找到记录所在的块,再从块中找
-
哨兵法:省略对下标越界的检查,提高算法执行速度
-
折半查找(二分查找)
- 前提:有序,顺序存储
- 判定树: n n n个节点,最多判定 ? log ? 2 n ? + 1 \lfloor\log_2{n}\rfloor+1 ?log2?n?+1次
- A S L = n + 1 n log ? 2 ( n + 1 ) ? 1 ≈ log ? 2 ( n + 1 ) ? 1 ASL=\frac{n+1}{n}\log_2(n+1)-1\approx\log_2(n+1)-1 ASL=nn+1?log2?(n+1)?1≈log2?(n+1)?1
- 只适用于有序表的顺序存储
- 效率很高
-
索引顺序表
- 索引:把一个关键字与它对应的记录相关联的过程
- 索引存储结构:数据主表,索引表
- 索引项的一般形式:关键字值+地址
- 主表:用数组存待查记录,每个数据元素至少有一个关键字域
- 索引表:按关键字有序,表中每个节点有最大关键字域和指向本块的第一个节点的指针
- 块间有序,块内无序
- 第 i + 1 i+1 i+1个块的关键字均大于(小于)第 i i i个块的记录关键字
- A S L = log ? 2 ( n s + 1 ) + s 2 ASL=\log_2(\frac{n}{s}+1)+\frac{s}{2} ASL=log2?(sn?+1)+2s?(长度为n的表分为b块,每块有s个记录)
-
二叉排序树
- 左小右大
- 中序遍历二叉排序树得到增序列
- 插入,删除都保持有序性
-
平衡二叉树(AVL树)
- 平衡因子(Balance Factor):左子树高度减右子树高度
- 平衡化旋转
- 单向:单向左旋,单向右旋
- 双向:先左后右,先右后左
- 适合查找,较少插入和删除
-
B树(多路平衡查找树)
- B-:非终端节点至少有
?
m
2
?
\lceil\frac{m}{2}\rceil
?2m??棵子树,最多有
m
m
m棵子树
- 叶子节点都同一层次且不包含任何信息
- 若 m m m阶B-树中有 N N N个关键字,则叶子节点(查找不成功的节点)有 N + 1 N+1 N+1个
- B-:非终端节点至少有
?
m
2
?
\lceil\frac{m}{2}\rceil
?2m??棵子树,最多有
m
m
m棵子树
-
B+树
- 一个节点有 N N N个关键字,则一定有 N N N棵子树
- 叶子节点按小到大链接
- 叶子结点包含了全部记录的关键字信息以及关键字记录的指针
- 非终端节点中只含有其子树根节点中最大最小关键字
-
哈希
- 哈希存储:数组存储
- 哈希函数:关键字与对应地址的联系(哈希函数是一个压缩映象)
- 直接定址法:关键字的线性函数,仅适用于地址集与关键字集等大
- 数字分析法:选几位
- 平方取中法:适用于关键字中(比较常用)
- 折叠法:移位相加,间界相加(类似蛇形)从右向左分割 适用于关键字位数比较多,数字分布比较均匀的情况
- 除留余数法:最简单,最常用。(选择质数,或不含20以内质因子的合数)
- 设计哈希函数应考虑:
- 计算哈希函数所需时间
- 关键字长度
- 哈希表大小
- 关键字分布情况
- 记录查找频率
- 解决冲突
- 开放定址法:线性探测再散列,二次探测再散列,伪随机探测再散列。充分利用空间,但比较容易产生聚集
- 再哈希法:构造若干个哈希函数,不易聚集但增加计算时间
- 链地址法(拉链法):表前插入/表后插入
- 建立公共溢出区
- 哈希查找:按照处理冲突的方式查找,知道地址对应值为空
- 装填因子 α = 记 录 数 哈 希 表 长 \alpha=\frac{记录数}{哈希表长} α=哈希表长记录数?
- 线性探测再散列: A S L = 1 2 ( 1 + 1 1 ? α ) ASL=\frac{1}{2}(1+\frac{1}{1-\alpha}) ASL=21?(1+1?α1?)
- 二次探测再散列: A S L = ? 1 a ln ? ( 1 ? a ) ASL=-\frac{1}{a}\ln{(1-a)} ASL=?a1?ln(1?a)
- 链地址法: A S L = 1 + α 2 ASL=1+\frac{\alpha}{2} ASL=1+2α?
-
排序
- 性能评价:时间复杂度,辅助空间,稳定性
- 内部排序
- 插入排序
- 直接插入排序
- 稳定
- 最好情况:比较 n ? 1 n-1 n?1次 移动 0 0 0次
- 最差情况:比较 n ( n ? 1 ) 2 \frac{n(n-1)}{2} 2n(n?1)?次 移动 1 2 ( n ? 1 ) ( n + 4 ) \frac{1}{2}(n-1)(n+4) 21?(n?1)(n+4)次
- 希尔排序
- 不稳定
- 克服了直接插入排序每次只能交换相邻两个记录的缺点
- 直接插入排序
- 选择排序
- 简单选择排序
- 不稳定
- 辅助空间 O ( 1 ) O(1) O(1)
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 堆排序
- 不稳定
- 辅助空间 O ( 1 ) O(1) O(1)
- 时间复杂度 O ( n log ? n ) O(n\log{n}) O(nlogn)
- 简单选择排序
- 交换排序
- 冒泡排序
- 稳定
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 最坏比较次数 n ( n ? 1 ) 2 \frac{n(n-1)}{2} 2n(n?1)?,交换次数 3 n ( n ? 1 ) 2 \frac{3n(n-1)}{2} 23n(n?1)?
- 快速排序
- 不稳定
- 最好时间复杂度 O ( n log ? n ) O(n\log{n}) O(nlogn)
- 最坏时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 冒泡排序
- 归并排序
- 稳定
- 2路归并
- 辅助空间 O ( n ) O(n) O(n)
- 时间复杂度 O ( n log ? n ) O(n\log{n}) O(nlogn)
- 基数排序
- 稳定
- 时间复杂度 O ( d ( n + r a d i x ) ) O(d(n+radix)) O(d(n+radix))(关键字d位,每位基数radix,n个对象)
- 辅助空间 O ( n + r a d i x ) O(n+radix) O(n+radix)
- 插入排序
笔试题记不清了,只记得去年笔试附加题考了十字链表
写在后面
记得去年考数据结构时候焦头烂额,笔试前一天晚上通宵一晚整理复习了一本书。当时困得要死,好在后来结果差强人意。现在把当时笔记重新整理下分享出来,方便大家复习。大家加油嗷!!!