[数据结构与算法]MATLAB实现高斯混合分布的EM算法及二维时概率密度曲面、置信椭圆绘制

具体EM算法并不打算介绍太多，详细公式及证明可以参考文末链接的参考内容

EM算法

1 定义分量数目$K$,对每个分量$k$设置${\pi }_k,{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k$的初始值。
2 E step
根据当前的${\pi }_k,{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k$计算后验概率$\gamma (z_{nk})$。
$$\gamma \left(z_{nk}\right)=\frac{{\pi }_k\mathcal{N}\left({\mathbf{x}}_n\mid {\mathbf{\mu }}_n,{\mathbf{\Sigma }}_n\right)}{{\sum }_{j=1}^K{\pi }_j\mathcal{N}\left({\mathbf{x}}_n\mid {\mathbf{\mu }}_j,{\mathbf{\Sigma }}_j\right)}$$
3 M step
根据 E step 中计算的$\gamma (z_{nk})$再计算新的${\pi }_k,{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k$：
$$\begin{array}{rl}{\mathbf{\mu }}_k^{new}& =\frac{1}{N_k}\sum _{n=1}^N\gamma \left(z_{nk}\right){\mathbf{x}}_n\\ {\mathbf{\Sigma }}_k^{new}& =\frac{1}{N_k}\sum _{n=1}^N\gamma \left(z_{nk}\right)\left({\mathbf{x}}_n?{\mathbf{\mu }}_k^{new}\right){\left({\mathbf{x}}_n?{\mathbf{\mu }}_k^{new}\right)}^T\\ {\pi }_k^{new}& =\frac{N_k}{N}\end{array}$$
其中：
$$N_k=\sum _{n=1}^N\gamma \left(z_{nk}\right)$$
4 检查参数是否收敛或对数似然函数是否收敛，若不收敛，则返回第2步。
对数似然函数：
$$\ln p(\mathbf{x}\mid \mathbf{\pi },\mathbf{\mu },\mathbf{\Sigma })=\sum _{n=1}^N\ln \left\{\sum _{k=1}^K{\pi }_k\mathcal{N}\left({\mathbf{x}}_k\mid {\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k\right)\right\}$$

EM算法MATLAB实现（附带详细注释）

此EM算法代码利用大量矩阵运算，和反复转置，减小了中间变量的大小，显著提高效率。

function [Mu,Sigma,Pi,Class]=gaussKMeans(pntSet,K,initM)
% @author:slandarer
% ===============================================================
% pntSet  | NxD数组   | 点坐标集                                |
% K       | 数值      | 划分堆数量                              |
% --------+-----------+-----------------------------------------+
% Mu      | KxD数组   | 每一行为一类的坐标中心                  |
% Sigma   | DxDxK数组 | 每一层为一类的协方差矩阵                |
% Pi      | Kx1列向量 | 每一个数值为一类的权重(占比)            |
% Class   | Nx1列向量 | 每一个数值为每一个元素的标签(属于哪一类)|
% --------+-----------+-----------------------------------------+


[N,D]=size(pntSet); % N:元素个数 | D:维数

% 初始化数据===============================================================
if nargin<3
    initM='random';
end
switch initM
    case 'random' % 随机取初始值
        [~,tIndex]=sort(rand(N,1));tIndex=tIndex(1:K);
        Mu=pntSet(tIndex,:);

    case 'dis'    % 依据各维度的最大最小值构建方向向量
                  % 并依据该方向向量均匀取点作为初始中心       
        tMin=min(pntSet);
        tMax=max(pntSet);
        Mu=linspace(0,1,K)'*(tMax-tMin)+repmat(tMin,K,1);

    % case '依据个人需求自行添加'  
    % ... ...
    % ... ...     
end

% 一开始设置每一类有相同协方差矩阵和权重
Sigma(:,:,1:K)=repmat(cov(pntSet),[1,1,K]);
Pi(1:K,1)=(1/K);

% latest coefficient:上一轮的参数
LMu=Mu;        
LPi=Pi;
LSigma=Sigma;

turn=0; %轮次

% GMM/gauss_k_means主要部分================================================
while true
    
    % 计算所有点作为第k类成员时概率及概率和(不加权重)
    % 此处用了多次转置避免构建NxN大小中间变量矩阵
    % 而将过程中构建的最大矩阵缩小至NxD，显著减少内存消耗
    Psi=zeros(N,K);
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Psi(:,k)=((2*pi)^(-D/2))*(det(Sigma(:,:,k))^(-1/2))*...
                      exp(-1/2*sum((Y/Sigma(:,:,k)).*Y,2))';    
    end
    
    % 加入权重计算各点属于各类后验概率
    Gamma=Psi.*Pi'./sum(Psi.*Pi',2);
    
    % 大量使用矩阵运算代替循环，提高运行效率
    Mu=Gamma'*pntSet./sum(Gamma,1)';
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Sigma(:,:,k)=(Y'*(Gamma(:,k).*Y))./sum(Gamma(:,k));
    end
    Pi=(sum(Gamma)/N)';
    [~,Class]=max(Gamma,[],2);

    % 计算均方根误差
    R_Mu=sum((LMu-Mu).^2,'all');
    R_Sigma=sum((LSigma-Sigma).^2,'all');
    R_Pi=sum((LPi-Pi).^2,'all');
    R=sqrt((R_Mu+R_Sigma+R_Pi)/(K*D+D*D*K+K));
    
    % 每隔10轮输出当前收敛情况
    turn=turn+1;
    if mod(turn,10)==0
        disp(' ')
        disp('==================================')
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        disp('----------------------------------')
        disp(['均方根误差:',num2str(R)])
        disp('当前各类中心点：')
        disp(Mu)
    end
    
    % 循环跳出
    if (R<1e-6)||isnan(R)
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        if turn>=1e4||isnan(R)
            disp('GMM模型不收敛')
        else
            disp(['GMM模型收敛，参数均方根误差为',num2str(R)])
        end
        break;
    end
    
    LMu=Mu;
    LSigma=Sigma;
    LPi=Pi;
end
end

基本使用：

% 构造三个符合高斯分布的点集并合并
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([14 9],[1 0;0 1],500);
PntSet=[PntSet1;PntSet2;PntSet3];

% 构造GMM模型
tic
[Mu,Sigma,Pi,Class]=gaussKMeans(PntSet,3,'dis');
toc

对于1500组数据处理用时0.034s

二维高斯混合模型密度分布曲面绘制

高维高斯分布函数：
$$\begin{array}{c}\mathcal{N}(\mathbf{x}\mid \bar{u},\Sigma )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\exp \left[?\frac{1}{2}(\mathbf{x}?\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{?1}(\mathbf{x}?\mathbf{\mu })\right]\end{array}$$
高维混合分布函数：
$$p(\mathbf{x})=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(\mathbf{x}\mid {\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k\right)$$
高维混合分布函数生成函数：

function func=getGaussFunc(Mu,Sigma,Pi)
[K,D]=size(Mu);

X{D}=[];
for d=1:D
    X{d}=['x',num2str(d)];
end
X=sym(X);

func=0;
for k=1:K
    tMu=Mu(k,:);
    tSigma=Sigma(:,:,k);   
    tPi=Pi(k);
    tX=X-tMu;   
    func=func+tPi*(1/(2*pi)^(D/2))*(1/det(tSigma)^(1/2))*exp((-1/2)*(tX/tSigma*tX.'));
end

func=matlabFunction(func);
end

调用并绘图
此段代码承接上文基本使用处代码，并使用中EM算法生成的数据

% 构造概率密度函数
func=getGaussFunc(Mu,Sigma,Pi);

% 绘制概率密度图像
figure('Units','normalized','Position',[.3,.2,.6,.65])
[X1,X2]=meshgrid(0:.4:16,0:.4:12);
surf(X1,X2,func(X1,X2),'LineWidth',1)
%修饰一下
ax=gca;hold(ax,'on');
ax.XLim=[0,16];
ax.YLim=[0,12];
ax.LineWidth=2;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.ZMinorTick='on';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.ZColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=13;
ax.GridLineStyle='--';

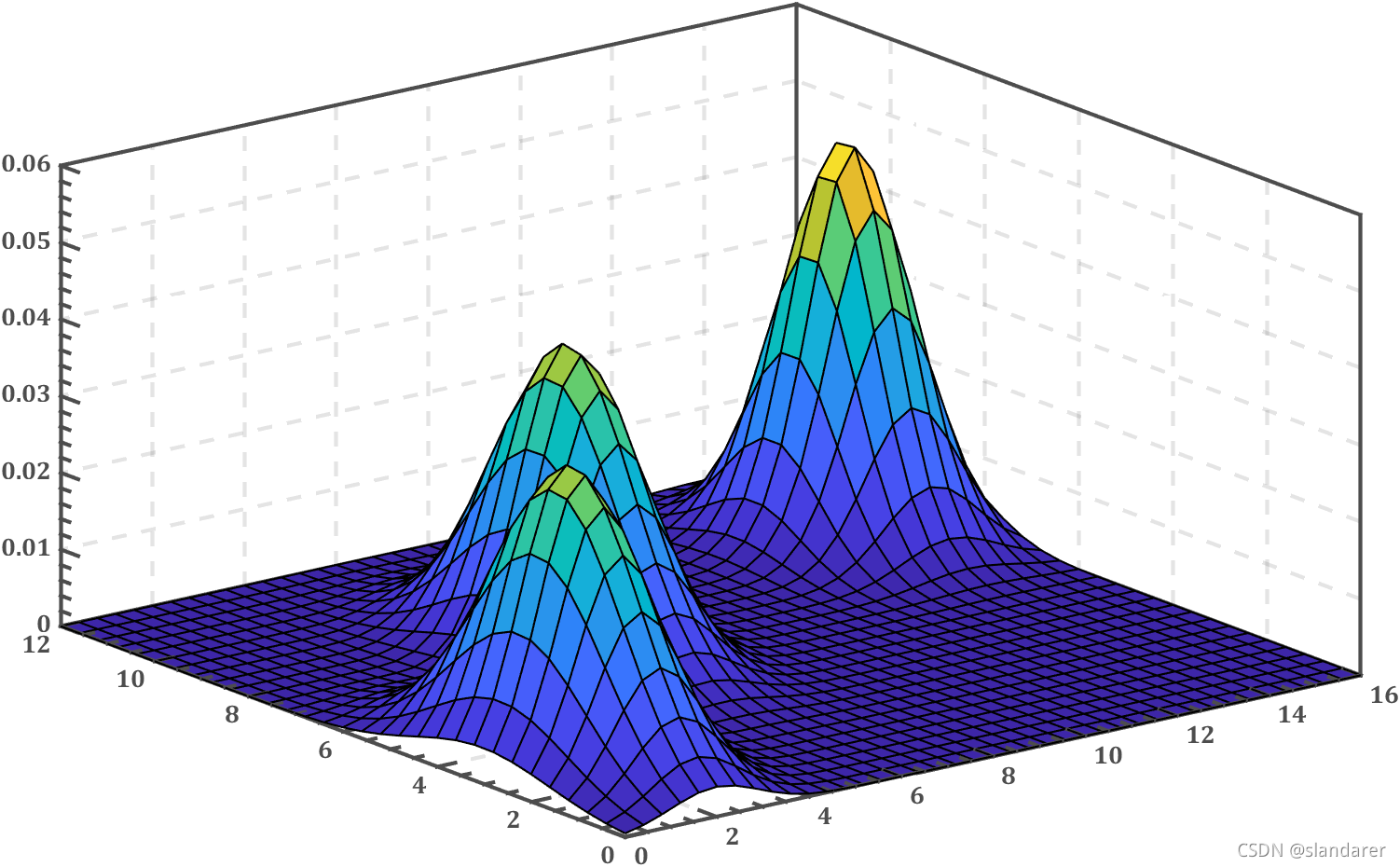
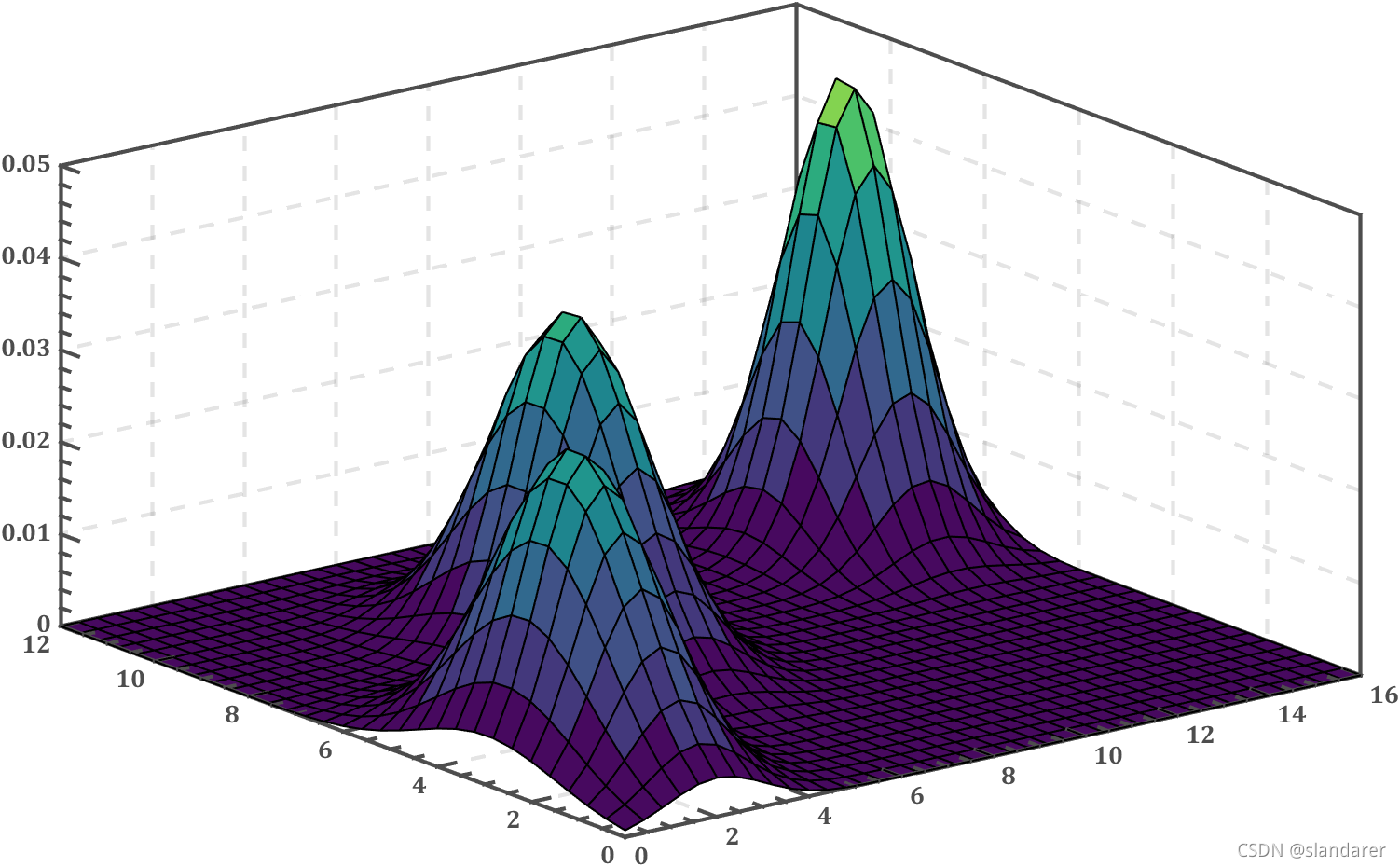
换个颜色：

散点分类情况及置信椭圆绘制

我们观察到，对每一个高维高斯分布，其自变量集中在exp()中
$$\begin{array}{c}\mathcal{N}(\mathbf{x}\mid \bar{u},\Sigma )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\exp \left[?\frac{1}{2}(\mathbf{x}?\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{?1}(\mathbf{x}?\mathbf{\mu })\right]\end{array}$$
也就是说函数数值完全随着括号内数值的变化而变化，
令
$$\begin{array}{c}(\mathbf{x}?\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{?1}(\mathbf{x}?\mathbf{\mu })\end{array}=S$$
实际为概率密度函数的一个等高线，且由于等式左侧的形式决定了此表达式是一个椭圆方程表达式，由于高维高斯分布积分较为困难，我们此时基于查表法确定右侧S值：95%:5.991，99%:9.21，90%:4.605

椭圆坐标生成函数：

function [X,Y]=getEllipse(Mu,Sigma,S,pntNum)
% 置信区间 | 95%:5.991  99%:9.21  90%:4.605
% (X-Mu)*inv(Sigma)*(X-Mu)=S

invSig=inv(Sigma);

[V,D]=eig(invSig);
aa=sqrt(S/D(1));
bb=sqrt(S/D(4));

t=linspace(0,2*pi,pntNum);
XY=V*[aa*cos(t);bb*sin(t)];
X=(XY(1,:)+Mu(1))';
Y=(XY(2,:)+Mu(2))';
end

绘制分类散点图及置信椭圆：
请根据分类个数改变colorList和循环的i值

% 绘制散点图
figure('Units','normalized','Position',[.3,.2,.5,.65])
ax=gca;hold(ax,'on');
colorList=[0.4  0.76 0.65
           0.99 0.55 0.38 
           0.55 0.63 0.80];
for i=1:3
    scatter(PntSet(Class==i,1),PntSet(Class==i,2),180,'filled',...
        'LineWidth',2.2,'MarkerEdgeColor',[1 1 1]*.3,'MarkerFaceColor',colorList(i,:));
end
% 绘制置信椭圆       
for i=1:3
    [X,Y]=getEllipse(Mu(i,:),Sigma(:,:,i),9.21,100);
    fill(X,Y,colorList(i,:),'EdgeColor',colorList(i,:).*.5,...
        'LineWidth',3,'FaceAlpha',.2)
    
end     
legend('pointSet1','pointSet2','pointSet3','conf.ellipse1','conf.ellipse2','conf.ellipse3')
%修饰一下
ax.XLim=[-2,18];
ax.YLim=[-2,14];
ax.LineWidth=2;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=15;
%ax.Color=[0.9,0.9,0.9];

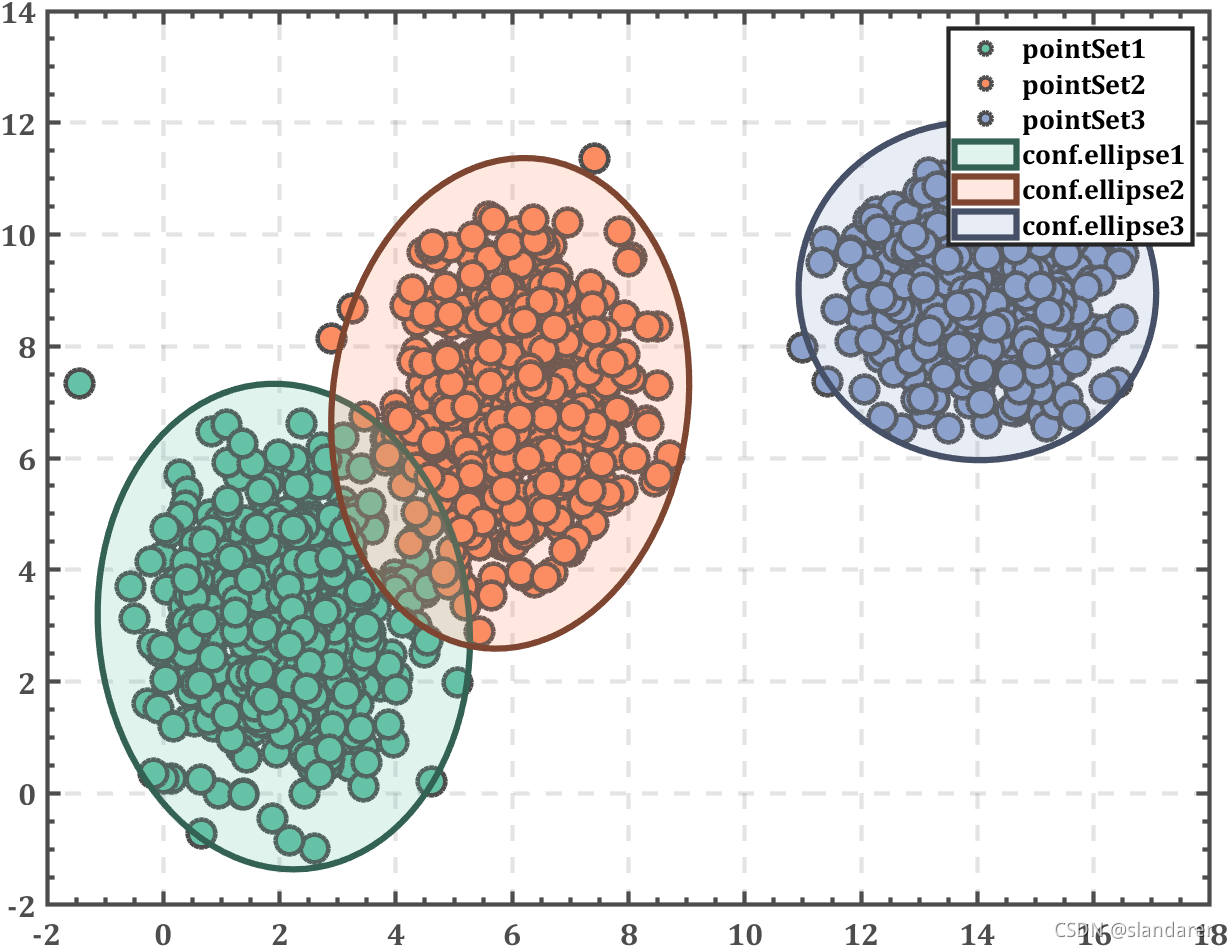
参考内容

EM算法过程：高斯混合模型（GMM）及其EM算法的理解

多维高斯公式推导及贝叶斯估计：
链接：PRML中文版_模式识别与机器学习.pdf
提取码：pd78