了解红黑树前,先认识一下二三树。
二三树:
普通的二叉树,一个节点存一个元素,有两个孩子,称为二树。 二三树中,允许一个节点存一个或两个元素,有两个或三个孩子。?


添加元素时,会与前面节点融合,当超过三个孩子时,向上融合。看看添加过程:
添加42:

?添加37,与前面节点融合,成为三树:

添加12,与前面节点融合,成为四树,不满足二三树,中位数向上与父亲融合,成为新的二三树:
 ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ?
?添加18:

?添加6:左孩子不满足,12向上与父亲节点融合
 ? ? ? ?
? ? ? ?
?添加11:

?添加5: 左叶子节点不满足,6向上与父亲节点融合。? ?融合后,父亲节点不满足,中位数12再向上融合:
 ? ? ?
? ? ? ? ?
? ?
?这就是二三树添加元素的过程。??
在二三树中,节点最多可以有两个元素,三个孩子。? 红黑树是一颗二分搜索树,但是可以等价于二三树。怎么表示呢?
红黑树:
把二三树中多元素的节点,一个用红色表示,一个用黑色表示,中间用红线连起来,就成了红黑树。

等价于下图:
?
所以,在二三树节点中如果是一个元素,就对应红黑树的一个黑色节点;? ?如果是两个元素,就对应红黑树中一对红黑节点的关系:
 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
?那究竟谁是红色谁是黑色呢?? ?二三树中新添加的节点,需要向老节点融合在一起;对应红黑树中可以理解为 红色向黑色融合。? 所以新添加的节点为红色(换句话说,红色就代表要向父亲节点融合)。? ? 另外红黑树要求,红色节点要左倾斜(作为左孩子),如果新加的元素成为了当前节点的右孩子,需要对当前节点左旋转,如下:
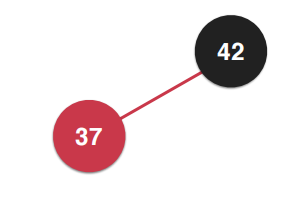
先添加37,再添加42。? ? ? 然后对37左旋转,最终如右图:
 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
红黑树定义:

?红黑树几个基本操作:
左旋:当节点左孩子为黑色(null也代表黑色),右孩子为红色,?不足满红色节点左倾斜。
旋转后,新的根节点颜色替换为原来根节点的颜色。 原来的根节点变成了孩子,需要变成红色,代表与新的根节点融合(因为要保持原二三树中两个元素融合在一起)。

右旋:当左孩子是红色,左孩子的左孩子也是红色,不满足第4点定义。另外红色代表向上融合在一起,在二三树中就相当于有三个元素融合在一个节点了,这时候要对42节点右旋,把元素变成独立节点的样子,右旋后新的根节点37颜色保持为老的根节点47的黑色。
但是,仅仅右旋,也只是三个元素已经有独立节点的样子了,还不能真正代表二三树中的独立节点,除非全部是黑色,但这时候12的颜色还是红色,所以他们依旧还是二三树中融合在一起的元素,既然融合在一起,42节点就要变为红色,才能代表与新的父亲节点37融合。
也就是说,右旋的操作,除了旋转外,还需要把新的根节点替换为原根节点的颜色,原根节点的颜色变为红色代表与新根节点融合。

颜色反转:左孩子是红色,右孩子也是红色(右旋之后就会这样)。? ?红色代表向上融合在一起,在二三树中就相当于有三个元素在一个节点了,所以要变成三个独立元素节点(三个都是黑色),但是父亲节点要继续往上融合,所以父亲节点变为红色,两个孩子变为黑色。
? ?
? ?
?
红黑树添加元素的过程:

?代码实现:
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node) {
if (node == null) {
return BLACK;
}
return node.color;
}
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node) {
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node) {
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value) {
root = add(root, key, value);
root.color = BLACK; // 最终根节点为黑色节点
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key, value); // 默认插入红色节点
}
if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
node.right = add(node.right, key, value);
} else // key.compareTo(node.key) == 0
{
node.value = value;
}
if (isRed(node.right) && !isRed(node.left)) {
node = leftRotate(node);
}
if (isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
if (isRed(node.left) && isRed(node.right)) {
flipColors(node);
}
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key) {
if (node == null) {
return null;
}
if (key.equals(node.key)) {
return node;
} else if (key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else // if(key.compareTo(node.key) > 0)
{
return getNode(node.right, key);
}
}
public boolean contains(K key) {
return getNode(root, key) != null;
}
public V get(K key) {
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue) {
Node node = getNode(root, key);
if (node == null) {
throw new IllegalArgumentException(key + " doesn't exist!");
}
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key) {
Node node = getNode(root, key);
if (node != null) {
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null) {
return null;
}
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
return node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
return node;
} else { // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空的情况
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
}时间复杂度: 如果二三树中有n个节点,复杂度是logn。? 如果每个节点都是三树(两个元素),也就是说红黑树中,每经过一个黑色节点,都要经过一个红色节点,红黑树的复杂度就是2logn。