机器学习04:利用朴素贝叶斯判别网络评论的情绪好坏(航空公司数据集)
文章目录
前言
在机器学习中许多分类算法通过一系列决策属性,边界(决策树,kNN算法,支撑向量机等)来对各个属性进行划分。然而这样的算法却经常会产生某类奇怪的分类错误,深究其原因很大可能是,算法依赖的决策边界过度依赖训练集。而我们今天介绍的算法朴素贝叶斯使用贝叶斯公式作为算法核心,区别于寻找决策边界计算后验概率,该算法反而去计算条件概率。这是什么意思呢?我们假设要分类下面这个网络评论:
“ 我真的好喜欢你啊啊啊啊啊啊啊啊啊啊啊,珈乐Carol!,为了你我要好好学习努力考研,做一个对社会有用的人!!!!!!!!!!!!!!!”
的好🥰坏😅。如果使用决策树方法我们可能会去寻找几个关键词然后决定它的种类。但是换成朴素贝叶斯方法,我们要去计算的假设他是一个不好的评论条件下,他是上面这串字符串的概率。同理我们也需要假设他是一个好的评论,他是上面这串字符串的概率。最后比较这两个概率的大小来决定他的评论分类是好🥰坏😅。
本篇博客算法代码以及开源,需要的话可以上github自取(liujiawen-jpg/Naive-Bayes: 使用朴素贝叶斯算法对航空公司评论数据集进行分类 (github.com))
1.算法理论分析
1.1贝叶斯公式
贝叶斯是欧洲中世纪著名的数学家,给概率论做出了巨大的贡献。他的著名的贝叶斯公式形式其实非常简单:
P
(
A
∣
B
)
=
P
(
B
,
A
)
P
(
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
P(A \mid B)=\frac{P(B, A)}{P(B)}=\frac{P(B \mid A) P(A)}{P(B)}
P(A∣B)=P(B)P(B,A)?=P(B)P(B∣A)P(A)?
这个公式我们来通俗地解释一下吧。我们假设现在给定字符串B:
“ 我真的好喜欢你啊啊啊啊啊啊啊啊啊啊啊,珈乐Carol!,为了你我要好好学习努力考研,做一个对社会有用的人!!!!!!!!!!!!!!!”
我们假设A是该评论属于赞赏这一类。我们现在要根据B字符串的数据计算该评论属于赞赏的概率P(A|B)。通过贝叶斯公式的转换,转而利用评论为赞赏类别的概率P(A)与当评论是赞赏概率时字符串内容是:
“ 我真的好喜欢你啊啊啊啊啊啊啊啊啊啊啊,珈乐Carol!,为了你我要好好学习努力考研,做一个对社会有用的人!!!!!!!!!!!!!!!”
的概率。这里我们介绍一个名词先验概率。其实就是利用过去的知识推导出来的概率。假设网络世界十年以来赞赏评论出现的概率是0.7,那么我们就认为这个P(A)=0.7。但是这里有一个问题P(B)的意思是上面这串字符串在所有评论出现的概率,这个是非常难求的。特别是在网络世界用户庞大的今天,我可以利用脚本刷评论,或者多个用户复制粘贴该评论,我们如果要去取这个概率是非常难的。那么我们可不可以不求这个呢?我们先来看另一个公式,我们假设批评类别😈为C的那么同理可得字符串B属于C类的概率为:
P
(
C
∣
B
)
=
P
(
B
,
C
)
P
(
B
)
=
P
(
B
∣
C
)
P
(
C
)
P
(
B
)
P(C \mid B)=\frac{P(B, C)}{P(B)}=\frac{P(B \mid C) P(C)}{P(B)}
P(C∣B)=P(B)P(B,C)?=P(B)P(B∣C)P(C)?
可以看到P(C|B) 与P(A|B)的分母都一样,那么我们比较大小只需要比较分子即可,分母不需要计算,也就是说:
P
(
A
∣
B
)
∝
P
(
B
∣
A
)
P
(
A
)
P(A \mid B) \propto P(B \mid A) P(A)
P(A∣B)∝P(B∣A)P(A)
1.2 朴素贝叶斯分类器(Na?ve Bayes Classifie)
那么什么是朴素贝叶斯分类器呢,为了更加通俗地解释这个例子。让我们继续使用例子来简单说明。我们对上面使用的字符串进行切分:
import re
import jieba.posseg as pseg
#对中文字符串更多详细操作大家可以查看我之前的博客 https://blog.csdn.net/theworld666/article/details/116904510
def word_slice(lines):
corpus = []
corpus.append(lines.strip())
stripcorpus = corpus.copy()
for i in range(len(corpus)):
stripcorpus[i] = re.sub("@([\s\S]*?):", "", corpus[i]) # 去除@ ...:
stripcorpus[i] = re.sub("\[([\S\s]*?)\]", "", stripcorpus[i]) # [...]:
stripcorpus[i] = re.sub("@([\s\S]*?)", "", stripcorpus[i]) # 去除@...
stripcorpus[i] = re.sub(
"[\s+\.\!\/_,$%^*(+\"\']+|[+——!,。?、~@#¥%……&*()]+", "", stripcorpus[i])
# 去除标点及特殊符号
stripcorpus[i] = re.sub("[^\u4e00-\u9fa5]", "",
stripcorpus[i]) # 去除所有非汉字内容(英文数字)
stripcorpus[i] = re.sub("原标题", "", stripcorpus[i])
stripcorpus[i] = re.sub("回复", "", stripcorpus[i])
stripcorpus[i] = re.sub("(完)", "", stripcorpus[i]) # 相当于replace
#这里先使用re库清洗数据,将不影响原文意思和特殊字符全部去除
onlycorpus = []
for string in stripcorpus:
if(string == ''):
continue
else:
if(len(string) < 5):
continue
else:
onlycorpus.append(string)
cutcorpusiter = onlycorpus.copy()
cutcorpus = onlycorpus.copy()
wordtocixing = [] # 储存分词后的词语
for i in range(len(onlycorpus)):
cutcorpusiter[i] = pseg.cut(onlycorpus[i])#切割单词
cutcorpus[i] = ""
for every in cutcorpusiter[i]:
cutcorpus[i] = (cutcorpus[i] + " " + str(every.word)).strip()
wordtocixing.append(every.word)
return wordtocixing
lenx=[]
content = ["我真的好喜欢你啊啊啊啊啊啊啊啊啊啊啊,珈乐Carol!,为了你我要好好学习努力考研,做一个对社会有用的人!!!!!!!!!!!!!!"]
for string in content:
if not isinstance(string,str):
continue
lines=word_slice(string)
print(lines)
输出结果: [‘我’, ‘真的’, ‘好’, ‘喜欢’, ‘你’, ‘啊啊啊’, ‘啊啊啊’, ‘啊啊啊’, ‘啊’, ‘啊’, ‘珈’, ‘乐’, ‘为了’, ‘你’, ‘我’, ‘要’, ‘好好学习’, ‘努力’, ‘考研’, ‘做’, ‘一个’, ‘对’, ‘社会’, ‘有用’, ‘的’, ‘人’]
由于我们的评论大部分是中文,所以我们在切分中删除所有标点符号中英文。可以看到我们输出的结果是一堆单词的组合列表这可以看成我们的输入数据x,那么根据上面的公式我们求取的概率转化为
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
∣
c
)
P
(
x
)
P(c \mid \mathbf{x})=\frac{P(c) P(\mathbf{x} \mid c)}{P(\mathbf{x})}
P(c∣x)=P(x)P(c)P(x∣c)?
P?先验概率已知,P(x)不必求。那么现在最终我们还没求出来的就是P(x|c)。这个概率的意思是,当我类别是C的时候,我们产生x这一列表的概率。这怎么求呢?这时候我们就得使用朴素贝叶斯方法了。朴素贝叶斯假设所有决策属性全部都是相互独立互不影响的。也就是我们常说的
P
(
A
,
B
)
=
P
(
A
)
P
(
B
)
P(A,B) = P(A)P(B)
P(A,B)=P(A)P(B)
那么也就是说我们上面的一堆单词中所有单词都是互不影响的。例如当"社会"这个单词出现后,“有用“这个单词的出现跟他没有任何关系,或者是关系非常小所以我们完全忽略他。那么通过以上这些假设我们最终将问题转化为:
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
∣
c
)
P
(
x
)
=
P
(
c
)
P
(
x
)
∏
i
=
1
d
P
(
x
i
∣
c
)
P(c \mid \mathbf{x})=\frac{P(c) P(\mathbf{x} \mid c)}{P(\mathbf{x})}=\frac{P(c)}{P(\mathbf{x})} \prod_{i=1}^{d} P\left(x_{i} \mid c\right)
P(c∣x)=P(x)P(c)P(x∣c)?=P(x)P(c)?i=1∏d?P(xi?∣c)
那么怎么求P(x|c)呢?我们下面继续来探求。
1.3 词集模型和词袋模型
现在我们的问题转化到了如何求解xi属性出现在C类中的概率。这个怎么求呢?我们可以统计所有C类别中的词组。假设我将训练集中所有属于C类别的D条文本的单词全部整合成一个含有n个词的字典。那么这个时候我们可以求得:
p
(
x
i
∣
c
)
=
∣
D
c
,
x
i
∣
∣
D
c
∣
D
c
表
示
训
练
集
中
属
于
C
类
别
的
集
合
∣
D
c
,
x
i
∣
表
示
训
练
集
中
属
于
C
类
别
在
第
i
个
属
性
取
值
为
x
i
的
集
合
p\left(x_{i} \mid c\right)=\frac{\left|D_{c, x_{i}}\right|}{\left|D_{c}\right|}\\D_c表示训练集中属于C类别的集合\\|D_{c, x_{i}}| 表示训练集中属于C类别在第i个属性取值为x_i的集合
p(xi?∣c)=∣Dc?∣∣Dc,xi??∣?Dc?表示训练集中属于C类别的集合∣Dc,xi??∣表示训练集中属于C类别在第i个属性取值为xi?的集合
那么我们的问题就转化为统计所有属于C类别并且在第i个属性上取值为xi的数量,并最后除以全部C类别样本的数量,最后将所有属性的概率全部相乘就得到了我们的p(x|c).那么关于计算上面这个数量上有两张完全不同的方法。这就是我们下面介绍的词集模型和词袋模型。
1.3.1词集模型
我们首先利用所有训练文本创建一个含有所有单词的字典集合这里面没有任何重复的元素吧。假设有1000个单词。那么我们为了方便统一量化输入数据。我们将所有的句子全部处理为长度的一千的列表。这个列表完全忽视语序和单词出现次数的关系,单纯统计1000个单词出现在句子里的情况。出现为0不出现为1:
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document) #删除句子中重复的单词
return list(vocabSet) #返回不重复的含有训练集所有单词的词集
def setOfWords2Vec(vocabList, inputSet): #对所有输入数据构造词集
returnVec = [0]*len(vocabList) #初始化构造全0矩阵
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1 #该单词出现就记为1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
那么我们假设属于第C类第二个属性取值为“好"的句子有100条,第C类共有1000条句子,那么我们的概率就等于:
P
(
x
i
∣
c
)
=
100
/
1000
=
0.1
P(x_i \mid c) = 100/1000 = 0.1
P(xi?∣c)=100/1000=0.1
但是这个列表平完全忽视了单词出现次数对语义的影响,同一个单词多次出现说明该单词的意思在句子中可能是非常重要的(多次重复起强调作用),所以为了消除这个影响,我们使用了词袋模型对于这个问题进行改善。
1.3.2 词袋模型
词袋模型与上面一样也需要先构造所有单词组成的文本。然后对于输入数据,我们不是单纯地统计该单词是否出现而是统计所有单词出现的概率,我们还会统计输入单词出现的次数。他的逻辑可以用下面的图来形象表示。

构建他的代码只需要在词集代码上进行微调即可:
def bagOfWord2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for words in inputSet:
if words in vocabList:
returnVec[vocabList.index(words)]+=1
return returnVec
那么同上现在我们假设属于第C类第二个属性取值为“好"的句子有100条,第C类共有1000条句子(假设内容与上面一致)。这一百条句子中含有1000个” 好 “,1000条句子中有100000个词那么我们的概率就等于:
P
(
x
i
∣
c
)
=
1000
/
100000
=
0.01
P(x_i \mid c) = 1000/100000 = 0.01
P(xi?∣c)=1000/100000=0.01
可以看到这两个返回的结果是不一致的,在对于具体问题选择合适算法来选择到底是词集算法还是词袋算法显得尤为重要。
? 算法到这里理论已经进行到了尾声😲,但是计算机工程师后期在算法实践的时候该算法出现了一定的问题,所以学者又对他们进行了一定程度的优化
1.4 拉普拉斯修正
我们假设"丑陋"这个单词从来没有在训练集C类样本中出现过,但是现在验证集出现了我们的计算会出现什么问题呢?很显然我们的统计改词的概率为0.一个0在一个乘式中会使最终乘积为0.那么无论他后面有什么属性都于事无补。如果我们的句子是这样的:
? “世间最可爱的嘉然和一个魂击败了挖掘机的丑陋计划”
这句话显然是对他人的赞美,但是上述文章提到的影响直接使这句话被判为批评类别。针对这个影响最终我们使用拉普拉斯修正方法来进行误差修正,贝叶斯公式修正为:
P
^
(
c
)
=
∣
D
c
∣
+
1
∣
D
∣
+
N
P
^
(
x
i
∣
c
)
=
∣
D
c
,
x
i
∣
+
1
∣
D
∣
+
N
i
\hat{P}(c)=\frac{\left|D_{c}\right|+1}{|D|+N} \quad \hat{P}\left(x_{i} \mid c\right)=\frac{\left|D_{c, x_{i}}\right|+1}{|D|+N_{i}}
P^(c)=∣D∣+N∣Dc?∣+1?P^(xi?∣c)=∣D∣+Ni?∣Dc,xi??∣+1?
其中N,Ni为C属性能够取值的种类数。为了防止Dc为0,我们对分子进行加一处理。通过这样我们消除了由于训练集可能导致的严重失误。但是这里其实还有一个问题那就是多个非常小的数(假设1000个)相乘这个在数学上是有意义且可以计算的。但在计算机中现代编程语言对于浮点数是有最小下限值的。哪怕是0.1的1000次方都非常小难以继续用浮点数表示。所以这里我们使用对数运算来修正。
1.5 使用对数运算防止下溢出
在代数中有ln(a*b) = ln(a)+ln(b),因此可以把条件概率累乘转化成对数累加。其实之所以能这么计算结果也不会有太大的误差是因为y=x 与 y=lnx 两者的增减性函数性质是一致的:
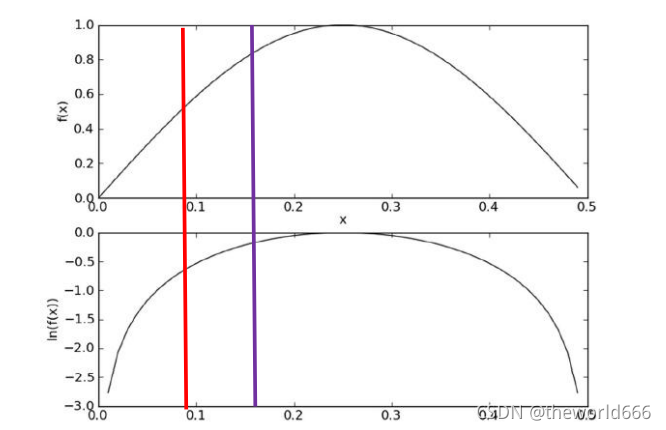
分类结果仅需对比概率的对数累加法 运算后的数值,以确定划分的类别 。最终我们的公式转化为:
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
∣
c
)
P
(
x
)
∝
[
l
n
(
P
(
c
)
)
+
∑
i
=
1
d
l
n
(
P
(
x
i
∣
c
)
)
]
P(c \mid \mathbf{x})=\frac{P(c) P(\mathbf{x} \mid c)}{P(\mathbf{x})} \propto [{ln(P(c))} + \sum_{i=1}^{d} ln(P\left(x_{i} \mid c\right))]
P(c∣x)=P(x)P(c)P(x∣c)?∝[ln(P(c))+i=1∑d?ln(P(xi?∣c))]
理论我们到这里就彻底介绍完了。那么现在就到了我们使用算法进行实践的时候了。让我们先来介绍我们本次的数据集。
2. 数据集预处理
本次实验我们采用美国航空公司对Tweet上对他们公司评价进行汇总的数据集(下载地址:Twitter US Airline Sentiment | Kaggle),人为的给每个评论都标上标签,一共有三个标签neural(中立的),positive(积极地),negative(消极的)。

本次我们实验只选取所有积极的评论和相同数量的消极评论来使用朴素贝叶斯分类器进行训练。他的数据格式为csv数据记载了非常多的属性所以我们在此次处理的时候只选用text评论文本,和sentiment情绪属性用于分类:
import pandas as pd
data = pd.read_csv('Tweets.csv')
data = data[['airline_sentiment', 'text']] #读取数据评论文本和标签属性
data.airline_sentiment.value_counts() #查看标签的数据分布
输出结果:
negative 9178
neutral 3099
positive 2363
可以看到这个航空公司不太行啊😂😂,14000多条评论数据集9178条是对它不好的评论。如果我们训练的是神经网络的话,这个时候其实我们该让数据分布一致集所有的数据一致才不会让神经网络在分类的时候影响分类结果(使用循环神经网络处理该数据集也可以:RNN学习:利用LSTM,GRU层解决航空公司评论数据预测问题_theworld666的博客-CSDN博客)。但我们如果使用的是贝叶斯的话,我们为了获得更加真实的先验概率不应该做这样的处理。所以我在这里最终是使用全部的消极数据和全部的积极数据进行处理:
sentiment_to_index = {'positive': 1, 'negative': 0}
def to_index(sentiment): # 利用函数转化标签
return sentiment_to_index.get(sentiment)
data_good = data[data.airline_sentiment == 'positive']
data_negative = data[data.airline_sentiment == 'negative']
dataSet = pd.concat([data_good,data_negative]) #将两个数据整合在一起
dataSet['sentiment'] = dataSet.airline_sentiment.apply(to_index) #将标签替换回0和1
del dataSet['airline_sentiment'] # 删除原有的一列
dataSet = dataSet.sample(len(dataSet)) #数据集进行打乱处理
那么我们的数据集最终便处理完成了,再将数据转化为词集或者词袋模型前,我们先来针对该数据集编写一下朴素贝叶斯分类器代码。
3.朴素贝叶斯算法代码
def trainNB0(trainMatrix, trainCategory):
numTrainDocs = len(trainMatrix) #trainMatrix是输入数据转化为词集后的集合
numWords = len(trainMatrix[0]) #统计每个元素的长度
pAbusive = np.sum(trainCategory)/np.float(numTrainDocs) #计算消极评论的先验概率
p0Num = np.ones(numWords)
p0Demon = 2.0
p1Num = np.ones(numWords) #由于拉普拉斯修正的原因创造全1矩阵和分母初始值为2
p1Demon = 2.0
for i in range(numTrainDocs):
if trainCategory[i] ==1:
p1Num +=trainMatrix[i]
p1Demon += np.sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Demon+= np.sum(trainMatrix[i]) #分别统计第0类和第一类单词的总数量
p1Vect = np.log(p1Num/p1Demon)
p0Vect = np.log(p0Num/p0Demon)#为了防止太多太小的数相乘导致下溢出所以取对数处理
return p0Vect,p1Vect,pAbusive #返回第0类和第一类每个单词的概率和第一类评论的先验概率
#利用给定的矩阵,以及变量进行分类
def classifyNB(vec2Classify, p0Vec, p1Vec, p1Class):
p0 = np.sum(vec2Classify*p0Vec)+np.log(1.0-p1Class) #二分类p0Class = (1.0-p1Class)
p1 = np.sum(vec2Classify*p1Vec)+np.log(p1Class)
if p0 > p1:
return 0
else:
return 1
通过上面我们就完成了拉普拉斯修正下的朴素贝叶斯算法的编写,可以看到其实代码非常简单,所以其实贝叶斯的好处就是运算速度其实非常快也非常容易修改嵌入。那么我们现在进行测试运行并对最终结果进行分析。
4.测试并评估结果
我们在第2步的数据集预处理下进一步编写代码如下:
import re
token = re.compile('\\w*') #使用预编译加快匹配速度
def textParse(bigString):
listOfToken = token.findall(bigString)
return [str.lower() for str in listOfToken if len(str)>0] #最终返回所有单词
#创建含有训练集所有单词的词集
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document) #删除句子中重复的单词
return list(vocabSet)
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
def airlineSentimentTest(dataSet):
dataStr = np.array(dataSet['text']).tolist() #将文本数据利用列表存储
docList = [textParse(sentence) for sentence in dataStr]
classList = np.array(dataSet['sentiment']).tolist() #将所有标签数据使用列表存储
vocabList = createVocabList(docList)
testNum = int(len(classList)*0.3) #取百分之三十的数据做测试集
testData = docList[:testNum] #由于数据集提前打乱,所以直接取前百分之三十即可
testClassList = classList[:testNum]
trainData = docList[testNum:]
trainClassList = classList[testNum:]
trainMat = []
for data in trainData:
trainMat.append(setOfWords2Vec(vocabList,data)) #遍历数据集将所有数据集使用词集模型来表示
p0V, p1V, pSPam = trainNB0(np.array(trainMat), np.array(trainClassList)) #通过训练数据集采集先验概率等一系列模型
errorCount = 0
for i in range(len(testData)): #统计测试集所有错误个数
wordVector = setOfWords2Vec(vocabList, testData[i])
if classifyNB(np.array(wordVector), p0V, p1V, pSPam)!= testClassList[i]:
errorCount+=1
result = float(errorCount)/len(testData) #计算错误率
print("错误率是: %.3f" % result)
return result
#循环十次计算平均错误率
for i in range(10):
dataSet = dataSet.sample(len(dataSet)) #每次循环都提前打乱数据
errorSum += airlineSentimentTest(dataSet)
errorSum /= 10.0 #计算平均错误率吧
print("平均错误率是%.3f" % errorSum)
使用词集模型最终分类结果为:
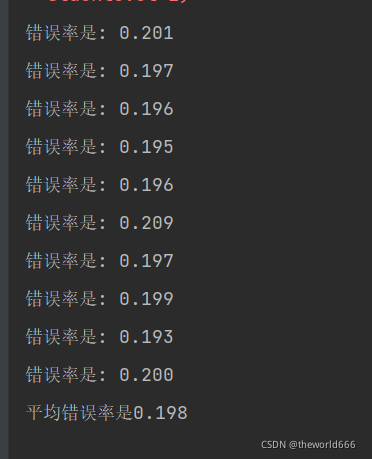
可以看到最终分类错误率仅有0.10,对于二分类来说这个其实是非常优秀的准确率。
我们如果使用词袋模型的方法来计算呢?这里需要注意一件事,使用词袋模型后的拉普拉斯修正需要经过修改。因为原有公式中
P
^
(
c
)
=
∣
D
c
∣
+
1
∣
D
∣
+
N
P
^
(
x
i
∣
c
)
=
∣
D
c
,
x
i
∣
+
1
∣
D
∣
+
N
i
\hat{P}(c)=\frac{\left|D_{c}\right|+1}{|D|+N} \quad \hat{P}\left(x_{i} \mid c\right)=\frac{\left|D_{c, x_{i}}\right|+1}{|D|+N_{i}}
P^(c)=∣D∣+N∣Dc?∣+1?P^(xi?∣c)=∣D∣+Ni?∣Dc,xi??∣+1?
Ni为属性xi可能取值个数,在词袋模型中他可以的取值个数是单词列表的长度+1所以我们修改代码如下
def trainNB0(trainMatrix, trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = np.sum(trainCategory)/np.float(numTrainDocs) #计算侮辱词语的概率
p0Num = np.ones(numWords)
p0Demon = numWords+1
p1Num = np.ones(numWords)
p1Demon = numWords+1 #这里拉普拉斯修正我们进行一些修改
for i in range(numTrainDocs):
if trainCategory[i] ==1:
p1Num +=trainMatrix[i]
p1Demon += np.sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Demon+= np.sum(trainMatrix[i])
p1Vect = np.log(p1Num/p1Demon)
p0Vect = np.log(p0Num/p0Demon)#为了防止太多太小的数相乘导致下溢出所以取对数处理
return p0Vect,p1Vect,pAbusive
def airlineSentimentTest(dataSet):
dataStr = np.array(dataSet['text']).tolist()
docList = [textParse(sentence) for sentence in dataStr]
classList = np.array(dataSet['sentiment']).tolist()
vocabList = createVocabList(docList)
print(len(vocabList))
testNum = int(len(classList)*0.3)
testData = docList[:testNum]
testClassList = classList[:testNum]
trainData = docList[testNum:]
trainClassList = classList[testNum:]
trainMat = [bagOfWord2VecMN(vocabList,data) for data in trainData]
# for data in trainData:
# trainMat.append(setOfWords2Vec(vocabList,data))
p0V, p1V, pSPam = trainNB0(np.array(trainMat), np.array(trainClassList))
errorCount = 0
for i in range(len(testData)):
wordVector = bagOfWord2VecMN(vocabList, testData[i])
# wordVector = setOfWords2Vec(vocabList, testData[i])
if classifyNB(np.array(wordVector), p0V, p1V, pSPam)!= testClassList[i]:
errorCount+=1
result = float(errorCount)/len(testData)
print("错误率是: %.3f" % result)
return result
通过这样的修改我们最终得出结果:
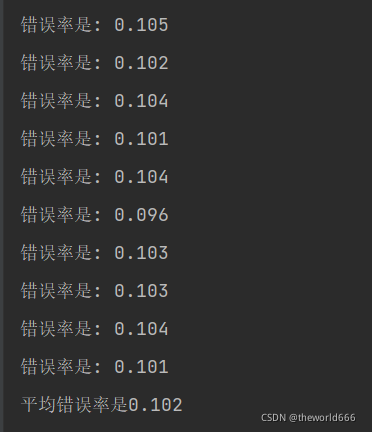
可以看到使用词袋模型的朴素贝叶斯算法取得更加优秀的成果,分类错误率仅仅只有百分之十。这说明了使用贝叶斯算法即使在如此复杂的数据集上也可以取得不错的效果同时贝叶斯算法也拥有计算速度快的优点。
结语
利用简单的概率论知识制作出有效快速的分类器。同时我们利用该算法在著名的航空公司评论数据集下利用词袋模型取得了只有10%错误率的优秀成绩。
这里也谈点题外话🤐🤐🤐通过对朴素贝叶斯算法的深度学习,我逐渐摆脱了对于任何问题全部求助于神经网络的想法,我了解到了如果要成为一名优秀的算法开发人员应该谨慎地选择每种算法兼顾考虑正确率速度来选择正确的算法,而机器学习比起深度神经网络在某些方面上依然是十分优秀的这是不容我们忽视的。
同时我逐渐了解到一系列机器学习算法对于数学的高度要求,让我从一开始抵触考研不想考研也逐渐开始理解考研对数学的高要求的原因。也是即使最终可能免试通过,但以我现在薄弱的数学基础,想在研究生阶段中在人工智能领域有所建树,做出些成果恐怕是非常困难的。所以也希望我个人可以利用这一年的时间扎实个人的数学基础。也希望我在一年后的研究生招生考试中取得优秀的成绩,考上理想中的学校。