文章目录
3.2 动态规划典型例题与解题思路(一)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rUnV4lCh-1637853110760)(C:/Users/26969/AppData/Roaming/Typora/typora-user-images/image-20211002210519339.png)]
分类是为了便于初学者理解,当熟练以后就没必要分开来看,都是动态规划。
一、拆分类
该类问题子问题比较清楚与起始终止位置无关而与自身长度有关。很容易看出“积木所在”通过组合下一级构造上一级。
1、矩阵连乘(极重要)
给定n个矩阵 { A 1 , A 2 , … , A n } \{A_1, A_2, …, A_n\} {A1?,A2?,…,An?},其中 A i A_i Ai?与 A i + 1 A_{i+1} Ai+1?是可乘的,i=1, 2,…, n-1。考察这n个矩阵的连乘积 A 1 A 2 … A n A_1A_2…A_n A1?A2?…An?。
由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
完全加括号的矩阵连乘积可递归地定义为:
①单个矩阵是完全加括号的;
②矩阵连乘积A是完全加括号的,则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号,即A=(BC)
设有四个矩阵A,B,C,D,可以有以下5种不同的加括号方式:
(A(B(CD))) (A((BC)D)) ((AB)(CD)) ((A(BC))D) (((AB)C)D)
每一种完全加括号方式对应于一种矩阵连乘积的计算次序,而矩阵连乘积的计算次序与其计算量有密切关系。矩阵A(p×q)和矩阵B(q×r)的乘积C=AB是一个p×r的矩阵,数乘次数为pqr
? 问题:
给定n个矩阵 { A 1 , A 2 , … , A n } \{A_1, A_2, …, A_n\} {A1?,A2?,…,An?},其中 A i A_i Ai?与 A i + 1 A_{i+1} Ai+1?是可乘的,i=1, 2,…, n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
1)穷举法
计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。
对于n个矩阵的连乘积,设其不同的计算次序为P(n)。由于每种加括号方式都可以分解为两个子矩阵的加括号问题:(A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下:
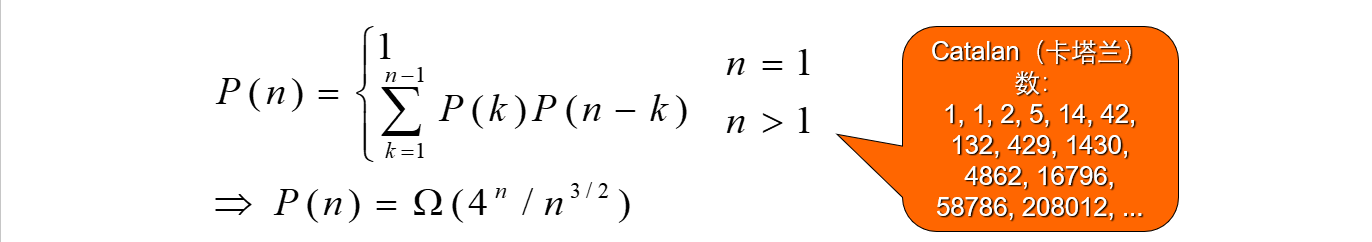
2)动态规划法
将矩阵连乘积AiAi+1…Aj简记为A[i:j] ,这里i≤j 。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,i≤k<j,则其相应完全加括号方式为:
( A i A i + 1 … A k ) ( A k + 1 A k + 2 … A j ) ( A_iA_{i+1}…A_k)(A_{k+1}A_{k+2}…A_j) (Ai?Ai+1?…Ak?)(Ak+1?Ak+2?…Aj?)
计算量:A[i:k]的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+1:j]相乘的计算量。
1?? 分析最优解的结构
特征:计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
2?? 建立递归关系
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
设Ai的维数为 p i ? 1 × p i p_{i-1}×p_i pi?1?×pi?,则
当i=j时, A [ i : j ] = A i A[i:j]=Ai A[i:j]=Ai,因此,m[i,i]=0,i=1,2,…,n
当i<j时, m [ i : j ] = m [ i , k ] + m [ k + 1 , j ] + p i ? 1 p k p j m[i:j]=m[i,k]+m[k+1,j]+p_{i-1}p_kp_j m[i:j]=m[i,k]+m[k+1,j]+pi?1?pk?pj?
可以递归地定义m[i,j]为:
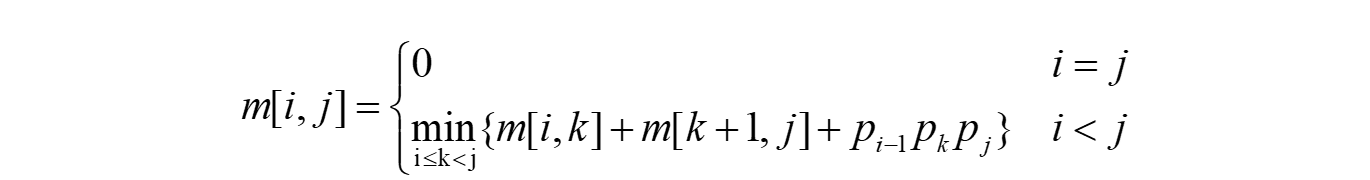
k的位置只有j-i种可能
3?? 计算最优值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此,不同子问题的个数最多只有
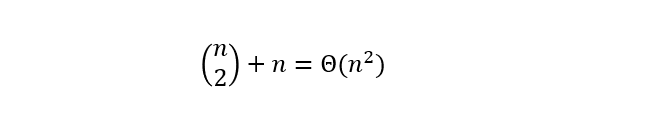
由此可见,在递归计算时,许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征
用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。
代码实现如下:
void matrixMutiply(int[] p, int n, int[][] m, int[][] s) {
for (int i = 1; i <= n; i++) {
//单一矩阵,无需计算
m[i][i] = 0;
}
for (int r = 2; r <= n; r++) {//对角线以上开始计算
for (int i = 1; i <= n - r + 1; i++) {
int j = r + i - 1;
//找m[i][j]的最小值,先初始化一下,令k=i
m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;//记录分割点
//k从i+1到j-1循环找m[i][j]的最小值
for (int k = i + 1; k < j; k++) {//k为分割点
int temp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (temp < m[i][j]) {
m[i][j] = temp;
s[i][j] = k;
}
}
}
}
}
算法复杂性分析:
算法MatrixChain的主要计算量取决于算法中对r,i和k的3重循环。循环体内的计算量为 O ( 1 ) O(1) O(1),而3重循环的总次数为 O ( n 3 ) O(n^3) O(n3)。因此算法的计算时间上界为 O ( n 3 ) O(n^3) O(n3)。算法所占用的空间显然为 O ( n 2 ) O(n^2) O(n2)。
4?? 构造最优解
由 s [ 1 ] [ n ] 的 值 可 知 A [ 1 : n ] 的 最 优 加 括 号 方 式 为 ( A [ 1 : s [ 1 ] [ n ] ] ) ( A [ s [ 1 ] [ n ] + 1 : n ] ) , 以 此 递 推 由s[1][n]的值可知A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n]),以此递推 由s[1][n]的值可知A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n]),以此递推
void traceBack(int i, int j, int[][] s) {
if (i == j) {
System.out.print("A" + i);
} else {
System.out.print("(");
traceBack(i, s[i][j], s);
traceBack(s[i][j] + 1, j, s);
System.out.print(")");
}
}
public static void main(String[] args) {
int[] p = {30, 35, 15, 5, 10, 20, 25};
int n = 6;
int[][] m = new int[7][7];
int[][] s = new int[7][7];
MatrixChain test = new MatrixChain();
test.matrixMutiply(p, n, m, s);
test.traceBack(1, 6, s);
System.out.println();
System.out.println(m[1][6]);
}
}
运算结果:
((A1(A2A3))((A4A5)A6))
15125
3)备忘录方法
备忘录方法的控制结构与直接递归方法的控制结构相同,区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
备忘录方法的递归方式是自顶向下的,而动态规划算法则是自底向上递归的。
int MemoizedMatrixChain(int []p,int n,int [][]m,int [][]s)
{
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
m[i][j]=0;
//0表示相应的子问题还末被计算
return LookupChain(1,n,p,m,s);
}
int LookupChain(int i,int j,int[]p,int[][]m,int [][]s)
{
if(m[i][j]>0) //大于0表示其中存储的是所要求子问题的计算结果
return m[i][j]; //直接返回此结果即可
if(i==j)
return 0;
int u=LookupChain(i,i,p,m,s)+LookupChain(i+1,j,p,m,s)+p[i-1]*p[i]*p[j];
s[i][j]=i;
for(int k=i+1;k<j;k++)
{
int t=LookupChain(i,k,p,m,s)+LookupChain(k+1,j,p,m,s)+p[i-1]*p[k]*p[j];
if(t<u)
{
u=t;
s[i][j]=k;
}
}
m[i][j]=u;
return u;
}
一般来讲,当一个问题的所有子问题都至少要解一次时,用动态规划算法比用备忘录方法好;当子问题空间中的部分子问题可不必求解时,用备忘录方法则较有利。
2、凸多边形最优三角剖分
用多边形顶点的逆时针序列表示凸多边形,即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。
若vi与vj是多边形上不相邻的2个顶点,则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…,vi}。
多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。
注意:T中各弦互不相交,且集合T已达到最大;有n个顶点的凸多边形的三角剖分中,恰有n-3条弦和n-2个三角形。
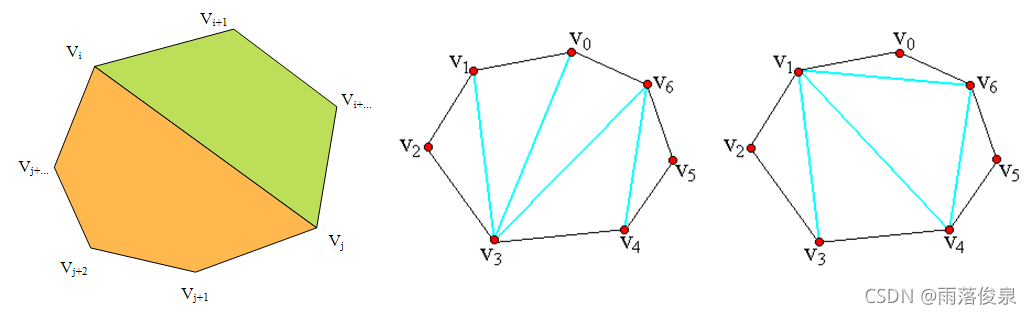
题目描述:给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权之和为最小。
① 三角剖分的结构
一个表达式的完全加括号方式相应于一棵完全二叉树,称为表达式的语法树。例如,完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6)))所相应的语法树如图 (a)所示。凸多边形{v0,v1,…vn-1}的三角剖分也可以用语法树表示。例如,图 (b)中凸多边形的三角剖分可用图 (a)所示的语法树表示。
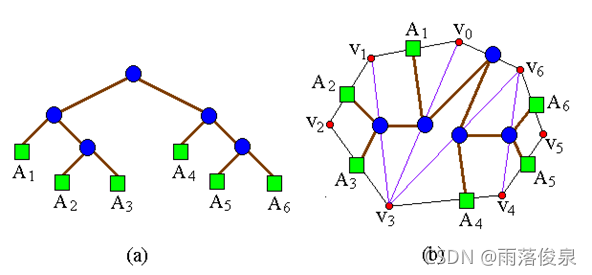
矩阵连乘积中的每个矩阵Ai对应于凸(n+1)边形中的一条边 v i ? 1 v i v_{i-1}v_i vi?1?vi?。三角剖分中的一条弦 v i v j v_iv_j vi?vj?,i<j,对应于矩阵连乘积A[i+1:j]。
给定矩阵链 A 1 A 2 A 3 A 4 A 5 A 6 A_1A_2A_3A_4A_5A_6 A1?A2?A3?A4?A5?A6?,Ai的维数为 p i ? 1 × p i p_{i-1}×p_i pi?1?×pi?;定义凸多边形P={ v 0 , v 1 , v 2 , v 3 , v 4 , v 5 , v 6 v_0,v_1,v_2,v_3,v_4,v_5,v_6 v0?,v1?,v2?,v3?,v4?,v5?,v6?},其三角形 v i v j v k v_iv_jv_k vi?vj?vk?上的权函数值为 w ( v i v j v k ) = p i p j p k w(v_iv_jv_k)=p_ip_jp_k w(vi?vj?vk?)=pi?pj?pk?,依此定义,P的最优三角剖分所对应的语法树给出了矩阵链的最优完全加括号方式。
② 最优子结构性质
凸多边形的最优三角剖分问题有最优子结构性质。
事实上,若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
③ 最优三角形剖分的递归结构
定义 t [ i ] [ j ] t[i][j] t[i][j],1≤i<j≤n为凸子多边形{vi-1, vi,…,vj}的最优三角剖分所对应的权函数值,即其最优值。为方便起见,设退化的多边形{vi-1,vi}具有权值0。据此定义,要计算的凸(n+1)边形P的最优权值为 t [ 1 ] [ n ] t[1][n] t[1][n]。
t [ i ] [ j ] t[i][j] t[i][j]的值可以利用最优子结构性质递归地计算。当j-i≥1时,凸子多边形至少有3个顶点。由最优子结构性质,** t [ i ] [ j ] t[i][j] t[i][j]**的值应为 t [ i ] [ k ] t[i][k] t[i][k]的值加上 t [ k + 1 ] [ j ] t[k+1][j] t[k+1][j]的值,再加上三角形 v i ? 1 v k v j v_{i-1}v_kv_j vi?1?vk?vj?的权值,其中i≤k≤j-1。由于在计算时还不知道k的确切位置,而k的所有可能位置只有j-i个,因此可以在这j-i个位置中选出使值 t [ i ] [ j ] t[i][j] t[i][j]达到最小的位置。由此, t [ i ] [ j ] t[i][j] t[i][j]可递归地定义为

④ 计算最优值
template<typename Type,typename E>
void MinWeightTriangulation(E *p,int n,Type **t,int **s)
{
for(int i=1; i<=n; i++)
t[i][i]=0;
for(int r=2; r<=n; r++)
for(int i=1; i<=n-r+1; i++)
{
int j=i+r-1;
t[i][j]=t[i+1][j]+w(p,i-1,i,j);
s[i][j]=i; //k=i
for(int k=i+1; k<i+r-1; k++)
{
int u=t[i][k]+t[k+1][j]+w(p,i-1,k,j);
if(u<t[i][j])
{
t[i][j]=u;
s[i][j]=k;
}
}
}
}
⑤ 构造最优三角剖分
s [ i ] [ j ] s[i][j] s[i][j]记录了与vi-1和vj一起构成三角形的第3个顶点的位置,据此可构造出最优三角剖分中的所有三角形。
template<typename E>
void Traceback(E *p,int i,int j,int **s)
{
if(i==j)
return;
int k=s[i][j];
cout<<p[i-1].v<<" "<<p[k].v<<" "<<p[j].v<<endl;
Traceback(p,i,k,s);
Traceback(p,k+1,j,s);
}
3、多边形游戏
多边形游戏是一个单人玩的游戏,开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值,每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。
1?? 游戏第1步,将一条边删除。
2?? 随后n-1步按以下方式操作:
(1)选择一条边E以及由E连接着的2个顶点V1和V2;
(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。
3?? 最后,所有边都被删除,游戏结束。游戏的得分就是所剩顶点上的整数值。
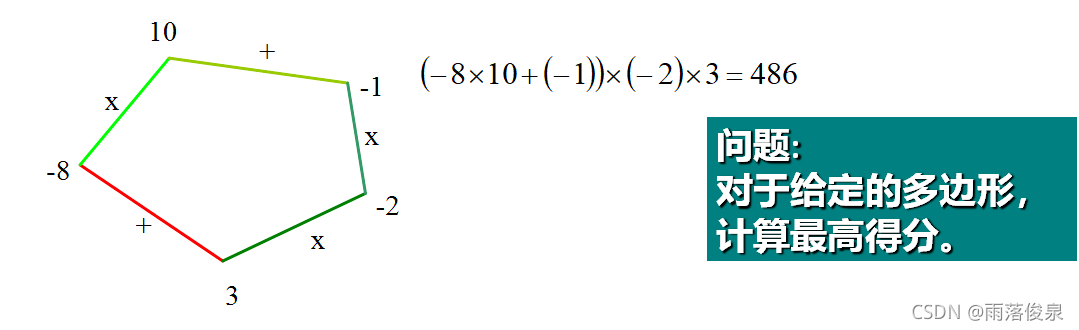
4、公园游艇问题(考试难度类似)
题目描述:长江游艇俱乐部在长江上设置了n 个游艇出租站{1,2,…,n}。游客可在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站 i 到游艇出租站 j 之间的租金为r(i,j),1≤i<j≤n。试设计一个算法,计算出从游艇出租站 1 到游艇出租站 n 所需的最少租金

1?? 最优解结构
r(i,j)表示游艇出租站i直接到j之间的租金,m(i,j)表示从出租站i出发,到达第j站需要的租金
例如m(1,3)就表示从第1站出发,到达第3站所需的租金,而m(1,3)可以有多种租用方案,例如可以1-2.2-3与1-3。
假设在第k站换游艇( i ≤ k ≤ j i\le k\le j i≤k≤j) ,则有m(i,j)=m(i,k)+m(k,j),其中m(i,j)的最优解包括m(i,k)与m(k,j)的最优解。
2?? 建立递归关系
由以上分析可知,显然有:
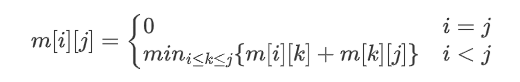
3?? 计算最优值
void cent(int[][] m, int n, int[][] s) {
for (int i = 1; i <=n ; i++) {
m[i][i]=0;
}
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n - r + 1; i++) {
int j = i + r - 1;
s[i][j] = i;
for (int k = i; k <= j; k++) {
int temp = m[i][k] + m[k][j];
if (temp < m[i][j]) {
m[i][j] = temp;
s[i][j] = k;//在第k站下
}
}
}
}
4?? 构造最优解
void traceBack(int i, int j, int[][] s) {
if (i == j) {
System.out.print(i);
return;
}
System.out.print("[");
traceBack(i, s[i][j], s);
traceBack(s[i][j] + 1, j, s);
System.out.print("]");
}