链接:https://ac.nowcoder.com/acm/problem/19427
来源:牛客网
题号:NC19427
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
给定一个序列,有多次询问,每次查询区间里小于等于某个数的元素的个数
即对于询问 (l,r,x),你需要输出 \sum_{i=l}^{r}[a_i \le x]∑
i=l
r
?
[a
i
?
≤x] 的值
其中 [exp] 是一个函数,它返回 1 当且仅当 exp 成立,其中 exp 表示某个表达式
输入描述:
第一行两个整数n,m
第二行n个整数表示序列a的元素,序列下标从1开始标号,保证1 ≤ ai ≤ 105
之后有m行,每行三个整数(l,r,k),保证1 ≤ l ≤ r ≤ n,且1 ≤ k ≤ 105
输出描述:
对于每一个询问,输出一个整数表示答案后回车
示例1
输入
复制
5 1
1 2 3 4 5
1 5 3
输出
复制
3
备注:
数据范围
1 ≤ n ≤ 105
1 ≤ m ≤ 105
首先简单讲讲我觉得理解树状数组代码几个比较重要的地方:
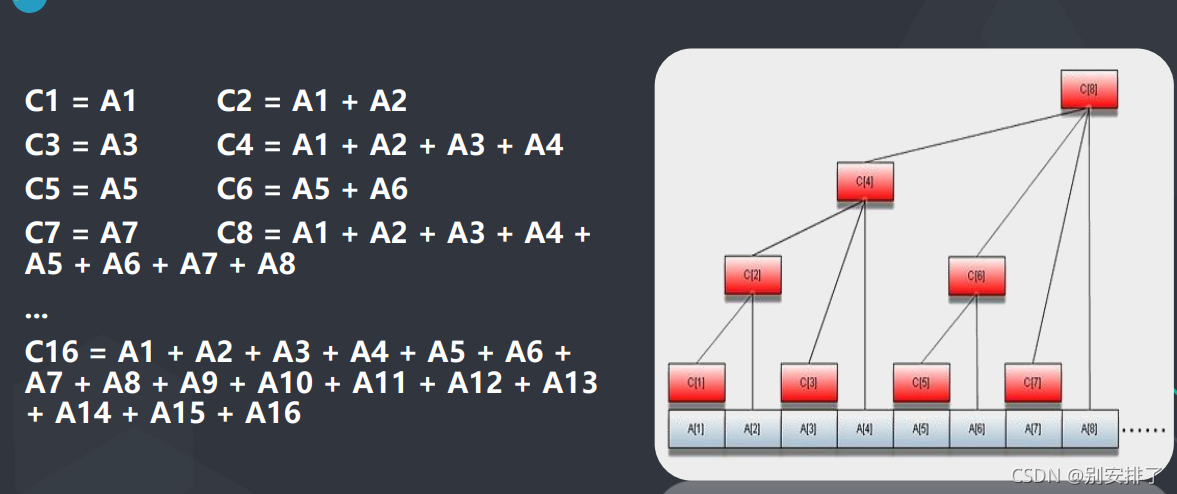
①:树状数组就是一个工具,为了优化修改,查询的工具
细节,看一看具体的实现函数
②:lowbit顾名思义就是求树状数组这个下标的最低二进制位,比方说c【8】,8的二进制表示是1000,所以呢他的lowbit是4,这个lowerbit有啥用处呢,我们直接观察这个树状数组,发现这个本位+lowbit就可以得到覆盖它的最小下标比方说c[8]+自身lowbit就可以得到c[16],减去自身的lowerbit就得到第一个他没有覆盖的区间,c[8]覆盖了8之前的全部区间,因此8-8=0;c[0]==0,所以树状数组还有个注意的地方就是必须预留出0的位置,从1开始。
所以呢,通过lowbit,我们可以得到add操作的刚好覆盖该点的树状数组节点,sum操作中刚好没有被该节点覆盖的点,实现修改与查询的功能。
怎么实现lowbit的功能,就是x&-x,看看计算机负数的存储就知道了。
③:懂了lowbit,add操作就是逐步将他的上一层修改就是了
④:懂了lowbit,sum操作就是查询之前所有的值就是了(通过lowbit实现了不重不漏)
⑤:几个小规律:最外面的节点是2^n,也就是覆盖了最上面所有的(前n个)节点;奇数节点一定是单个节点,偶数节点一定覆盖部分区域;在上述图例中体现了树状数组和原数组之间的关系。我们可以直接记住这个图,人脑可以调动图像化记忆,有助于提高学习效率
⑥:树状数组还有优化的技巧:比如离散化以及这篇的离线操作;不同的题目树状数组所对应的下标也是不同的,有的对应着值,有的对应着原来数组的下标,边学习边补充。
这道题目是求一个区间中<=某个特定的值的数量,给定区间范围i j,小于的数字k,我们按照k从小到大排序,再将a数组从小到大排序,在排序的同时记录下来所有的对应的原本的位置,按照排序的顺序从小到大枚举查询,从小到大枚举a数组,如果a【i】<=k,我们就add这个a[i]原本的位置,剩下的a[i]全部>k就查询,为啥这样可以呢?因为只有这样才能保证我们加上的数字都是有可能在该区间内的且一定比k小的数字这个树状数组的下标存放的是区间段端点。私以为:所谓离线操作就是我们针对查询(输入)进行调整从而更方便处理问题的过程。”离线“这种说法也很形象:在qq上我们收到离线信息,没有跟信息进行即时的交互,同样我们对这些查询也没进行即时的交互,而是对其缓存后续处理,是不是很形象…
看代码,stl熟练使用可以省不少的事情:
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<cstdio>
#include<stdlib.h>
#include<map>
#define M 500005
using namespace std;
int wo,wei,a[M],d[M],t[M],n,ming[M];
typedef pair<int,int>pii;
map<int,pii>ma;
priority_queue<pii,vector<pii>,greater<pii> >qu;
struct node
{
int va,dian;
bool operator<(const node& a)const
{
return va<a.va;
}
}node[M];
int lowbit(int x)
{
return x&-x;
}
void add(int x)//把包含这个数的结点都更新
{
while(x<=M)//范围
{
t[x]++;
x+=lowbit(x);
}
}//树状数组的下标必须从1开始
int sum(int x)
{
int res=0;
while(x>=1)
{
res+=t[x];
x-=lowbit(x);
}
return res;
}
int main()
{ int m;
long long ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
node[i].dian=i ;
node[i].va=a[i];
}
sort(node+1,node+n+1);
for(int i=1;i<=m;i++)
{
int l,r,zhi;
scanf("%d%d%d",&l,&r,&zhi);
qu.push({zhi,i});//i是第几次查询
ma[i]={l,r};//第i次查询的左右端点
} int i=1;
while(qu.size())
{
wo=qu.top().first;
wei=qu.top().second;
qu.pop();
if(i>n)
ming[wei]=sum(ma[wei].second)-sum(ma[wei].first-1);
while(i<=n)
{
if(node[i].va<=wo)
{
add(node[i].dian);
i++;
}
else
{
ming[wei]=sum(ma[wei].second)-sum(ma[wei].first-1);
break;
}
}ming[wei]=sum(ma[wei].second)-sum(ma[wei].first-1);
}
for(int i=1;i<=m;i++)
{
cout<<ming[i]<<endl;
}
return 0;
}