1、冒泡排序

首先从数组的第一个元素开始到数组最后一个元素为止，对数组中相邻的两个元素进行比较，如果位于数组左端的元素大于数组右端的元素，则交换这两个元素在数组中的位置，此时数组最右端的元素即为该数组中所有元素的最大值。算法的时间复杂度为O(n^2)。

*优化：每趟冒泡排序时判断一下是否交换过元素，如果没有交换过元素，证明已经有序，排序提前结束。

方法一：循环实现冒泡排序

//循环实现冒泡排序
void BubbleSort1(int arr[], int length) {
	int ifswap;//每趟排序中是否交换过元素，未交换为0，交换为1
	for (int i = 0; i < length - 1; i++) {//i为排序的趟数
		ifswap = 0;//每趟排序需初始化交换标志
		for (int j = 0; j < length - i - 1; j++) {
			if (arr[j] > arr[j + 1]) {//若前面的值大于其后的值，进行交换
				int temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
				ifswap = 1;
			}
		}
		if (ifswap == 0) return;
	}
}

方法二：递归实现冒泡排序?

//递归实现冒泡排序
void BubbleSort2(int arr[], int length) {
	int ifswap = 0;//每趟排序中是否交换过元素，未交换为0，交换为1
	if (length < 2) return;//数组小于2个元素不需要排序
	for (int i = 0; i < length - 1; i++) {
		if (arr[i] > arr[i + 1]) {
			int temp = arr[i];
			arr[i] = arr[i + 1];
			arr[i + 1] = temp;
			ifswap = 1;
		}
	}
	if (ifswap == 0) return;
	BubbleSort2(arr, --length);
}

?2、选择排序

从头至尾扫描序列，找出最小的元素，和第一个交换，接着从剩下的元素中继续查找交换，直至得到一个有序序列。算法的时间复杂度为O(n^2)。

//选择排序
void SelectionSort(int arr[], int length){
	int flag;
	for (int i = 0; i < length-1; i++) {//一共进行n-1趟比较
		flag = i;//记录最小元素的下标
		for (int j = i+1; j < length; j++) {//i之前的元素是已经排列好的
			if (arr[j] < arr[flag]) {
				flag = j;
			}
		}
		//如果本趟循环的最小值不是起始位置，则交换
		if (flag != i) {
			int temp = arr[i];
			arr[i] = arr[flag];
			arr[flag] = temp;
		}
	}
}

?*优化：将最小值和最大值都选出来，最小放在当前序列的最左边，最大放在当前序列的最右边，循环趟数可减半。

//选择排序的优化
void SelectionSort(int arr[], int length) {
	int left, right;//每趟排序的最左和最右的位置
	int minflag, maxflag;//记录最小和最大元素的下标
	int i;
	left = 0; right = length - 1;
	while (left < right) {
		minflag = maxflag = left;
		for (i=left; i <= right; i++) {//i之前的元素是已经排列好的
			if (arr[i] < arr[minflag])  minflag = i;
			if (arr[i] > arr[maxflag])  maxflag = i;
		}
		//如果本趟循环的最小值不是最左位置，则交换
		if (minflag != left) {
			int temp = arr[left];
			arr[left] = arr[minflag];
			arr[minflag] = temp;
		}
		if (maxflag == left) maxflag = minflag;
		//如果本趟循环的最大值不是最右位置，则交换
		if (maxflag != right) {
			int temp = arr[right];
			arr[right] = arr[maxflag];
			arr[maxflag] = temp;
		}
		left++, right--;
	}
}

3、插入排序

插入排序的基本思想就是将无序序列插入到有序序列中。对于未排序的数据，在已排序的序列中从后向前扫描，找到相应的位置后插入。该算法的时间复杂度为O(n^2)。

//插入排序
void InsertSort(int arr[], int length) {
	int tmp;//当前需要排序元素的值
	int i, j;
	for (i = 0; i < length; i++) {
		tmp = arr[i];//待排序元素
		for (j = i - 1; j >= 0; j--) {
			if (arr[j] <= tmp) break;
			arr[j + 1] = arr[j];//逐个元素后移
		}
		//插入当前排序元素
		arr[j + 1] = tmp;
	}
}

*优化：1、对已排序的序列进行二分查找法；2、携带多个元素；3、数据链表化

下面仅展示通过二分查找法实现的折半插入排序

//折半插入排序
void InsertSort(int arr[], int length) {
	int i, j, mid, left, right, t;
	for (i = 1; i < length; i++) {
		t = arr[i];
		for (left = 0, right = i - 1; left <= right;) {
			mid = (left + right) / 2;
			if (t < arr[mid]) right = mid - 1;
			else left = mid + 1
				;
		}
		for (j = i - 1; j >= left; j--)
			arr[j + 1] = arr[j];
		arr[left] = t;
	}
}

4、希尔排序

是对于直接插入排序的一种优化。先将待排记录序列分割成为若干子序列分别进行插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行一次直接插入排序。适用于较为庞大的数据排序

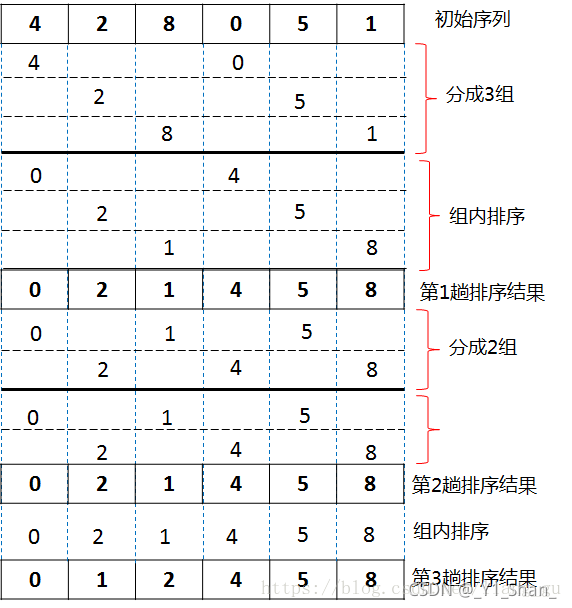
void groupsort(int arr[], int length, int pos, int step) {
	int t;//当前需要排序的元素的值
	int i, j;
	for (i = pos + step; i < length; i += step) {
		t = arr[i];
		//从已排序的最右开始，把大于当前排序的元素后移
		for (j = i - step; j >= 0; j -= step) {
			if (arr[j] <= t) break;
			arr[j + step] = arr[j];//逐个元素后移
		}
		arr[j + step] = t;//插入当前元素
	}
}
//希尔排序
void ShellSort(int arr[], int length) {
	int step, i;
	step = length / 2;//初始化时间间隔
	while (step > 0) {
		for (i = 0; i < step; i++) {
			groupsort(arr, length, i, step);
		}
		step /= 2;
	}
}

5、快速排序

通过一趟排序将待排记录分割成独立的两部分，从待排序列中任意选取一个数(通常选取第一个)作为基准值，然后将比它小的都安置在它的位置之前，将比它大的都安置在它的位置之后。

1、挖坑填数+分治

1、选出一个数据（一般是最左边或是最右边的）存放在key变量中，在该数据位置形成一个坑。
2、还是定义一个L和一个R，L从左向右走，R从右向左走。（若在最左边挖坑，则需要R先走；若在最右边挖坑，则需要L先走）。
3、在走的过程中，若R遇到小于key的数，则将该数抛入坑位，并在此处形成一个坑位，这时L再向后走，若遇到大于key的数，则将其抛入坑位，又形成一个坑位，如此循环下去，直到最终L和R相遇，这时将key抛入坑位即可。（选取最左边的作为坑位）

//快速排序（递归、挖坑法）
void QuickSort(int arr[], int start, int end) {
	if (start >= end) return;
	int left = start, right = end;
	int baseval = arr[start];//设置基准数
	while (left < right) {
		//right向左，找小
		while (left < right && arr[right] >= baseval)
			right--;
		if (left < right) {
			arr[left] = arr[right];
			left++;
		}
		//left向右，找大
		while (left < right && arr[left] <= baseval)
			left++;
		if (left < right) {
			arr[right] = arr[left];
			right--;
		}
	}
	//把基准数放到合适的位置
	arr[left] = baseval;
	//递归
	QuickSort(arr, start, left - 1);//递归基准数左边的元素
	QuickSort(arr, left + 1, end);//递归基准数左边的元素
}

2、hoarea法

1、选出一个key，一般是最左边或是最右边的。
2、定义一个L和一个R，L从左向右走，R从右向左走。（需要注意的是：若选择最左边的数据作为key，则需要R先走；若选择最右边的数据作为key，则需要L先走）。
3、在走的过程中，若R遇到小于key的数，则停下，L开始走，直到L遇到一个大于key的数时，将L和R的内容交换，R再次开始走，如此进行下去，直到L和R最终相遇，此时将相遇点的内容与key交换即可。（选取最左边的值作为key）

//hoare法实现快速排序
void Swap(int* x, int* y) {
	int temp = *x;
	*x = *y;
	*y = temp;
}
void QuickSort(int arr[], int start, int end) {
	//当只有一个数据或是序列不存在时，不需要进行操作
	if (start >= end) return;
	int left = start, right = end;
	int pos = left;//基准数下标
	while (left < right) {
		//right向前走，找小
		while (left < right && arr[right] >= arr[pos])
			right--;
		//left向后走，找大
		while (left < right && arr[left] <= arr[pos])
			left++;
		//交换left和right位置的值
		if (left < right)
			Swap(&arr[left], &arr[right]);
	}
	int meetpos = left;//left和right相等时的下标
	Swap(&arr[pos], &arr[meetpos]);//交换相遇点和基准数的值
	QuickSort(arr, start, meetpos - 1);//基准数左边的序列排序
	QuickSort(arr, meetpos + 1, end);//基准数右边的序列排序
}

6、归并排序

归并排序是典型的递归和分治的例子，具体是将已有序的子序合并，从而得到完全有序的序列，即先使每个子序有序，再使子序列段间有序。时间复杂度O(NlogN)。

void _MergeSort(int arr[], int arrtmp[], int start, int end) {
	if (start >= end)  return;//	区间元素少于两个，递归停止
	int mid = start + (end - start) / 2;

	int startpos1 = start, endpos1 = mid;//左区间内的首元素、最后一个元素位置
	int startpos2 = mid + 1, endpos2 = end;//右区间内的首元素、最后一个元素位置

	_MergeSort(arr, arrtmp, startpos1, endpos1);//对左区间递归排序
	_MergeSort(arr, arrtmp, startpos2, endpos2);//对右区间递归排序

	int i = start; 

	//把区间左右两边数列合并到已排序数列arrtmp中 
	while (startpos1 <= endpos1 && startpos2 <= endpos2)
		arrtmp[i++] = arr[startpos1] < arr[startpos2] ? arr[startpos1++] : arr[startpos2++];
	//把左边序列剩余部分追加到arrtmp中
	while (startpos1 <= endpos1) arrtmp[i++] = arr[startpos1++];
	//把右边序列剩余部分追加到arrtmp中
	while (startpos2 <= endpos2) arrtmp[i++] = arr[startpos2++];
	//把已排序数组arrtmp中的元素复制到arr中
	memcpy(arr + start, arrtmp + start, (end - start + 1) * sizeof(int));
}

//归并排序主函数
void MergeSort(int arr[], int length) {
	if (length < 2) return;//小于两个元素则不需要排序
	int* arrtmp = (int*)malloc(sizeof(int) * length);//申请一个与原数组大小相同的空间
	if (arrtmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	_MergeSort(arr, arrtmp, 0, length - 1);//归并排序
	free(arrtmp);//释放空间
}