一、概念
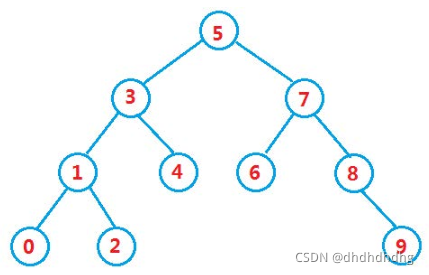
二叉搜索树又称二叉排序树,它可能是一棵空树,也可能是具有以下性质的二叉树:
1.若它的左子树不为空,则左子树上所有结点的值都小于根结点的值
2.若他的右子树不为空,则右子树上所有结点的值都大于根结点的值
3.它的左右子树也分别为二叉搜索树
例如下图:
二、操作——查找
步骤:
1.假如根结点不为空:
如果根结点.key==查找.key,返回true
如果根结点.key>查找.key,在其左子树中查找
如果根结点.key<查找.key,在其右子树中查找
2.如果为空,返回空
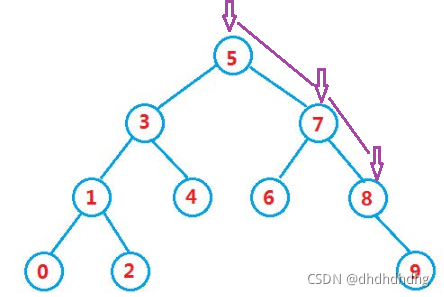
图象解释(假如在上面的二叉树中查找8)
代码实现:
public Node search(int key){
Node cur=root;
while(cur!=null){
if(key==cur.key){
return cur;
}else if(key<cur.key){
cur=cur.left;
}else{
cur=cur.right;
}
}
return null;
}
三、操作——插入
步骤:
1.如果树为空树,即根== null,直接插入:
返回true。
2.如果树不是空树,按照查找逻辑确定插入位置如果根结点.key==查找.key,与待插入结点key相等,不能插入,返回false
如果根结点>查找.key,在其左子树中查找
如果根结点<查找.key,在其右子树中查找
在查找的同时设置一个parent用来记录查找结点的双亲结点,方便后续的插入3.设置一个新结点进行插入(由于这里记录双亲结点不知道是左子树还是右子树,需要对key进行判断)
如果parent.key小于查找.key,parent的右子树是要插入的结点
如果parent.key大于查找.key,parent的左子树是要插入的结点返回true。
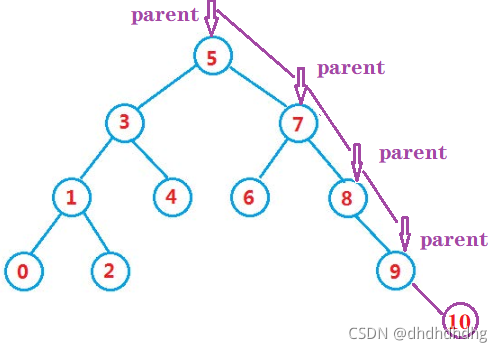
图象解释:(插入元素为10的新结点)
代码实现:
public boolean insert(int key){
//树为空,直接插入
if(root==null){
root=new Node(key);
return true;
}
//查找待插入结点位置
Node cur=root;
Node parent=null;
while(cur!=null){
if(key==cur.key){
return false;
}else if(key< cur.key){
parent=cur;
cur=cur.left;
}else{
parent=cur;
cur=cur.right;
}
}
//插入结点
Node node=new Node(key);
if(key<parent.key){
parent.left=node;
}else{
parent.right=node;
}
return true;
}
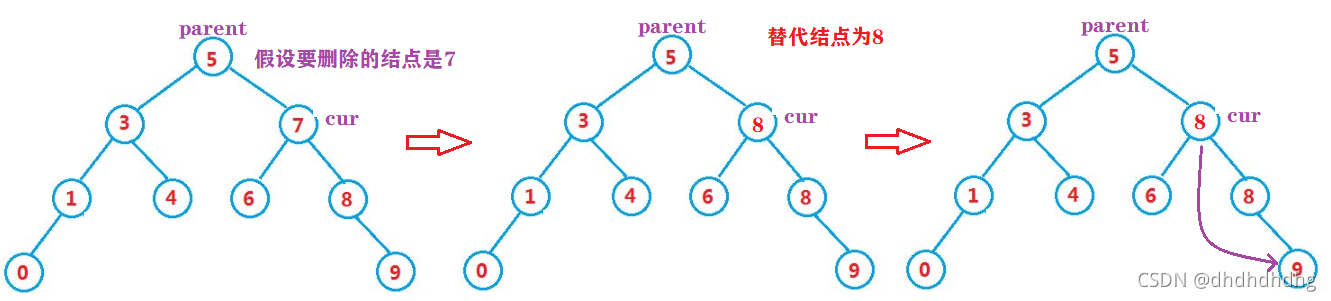
四、操作——删除(难点)
这里待删除的结点分四种情况:
1.叶子结点:cur.left == null&&cur.right == null
2.只有左子树:cur.left!=null&&cur.right == null
3.只有右子树:cur.left == null&&cur.right!=null
4.左子树右子树都有:cur.left!=null&&cur.right!=null
实际处理当中叶子结点或者只有右子树可以按照一种情况来处理
步骤:
1.找到待删除结点位置
2.如果走到null还没有找到则就是不在二叉搜索树中,返回false
3.之后判断此位置在哪,对上面三种情况分别进行处理
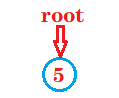
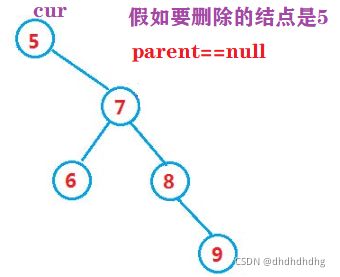
①叶子节点或者只有右子树:
cur是根结点:
root=cur.right
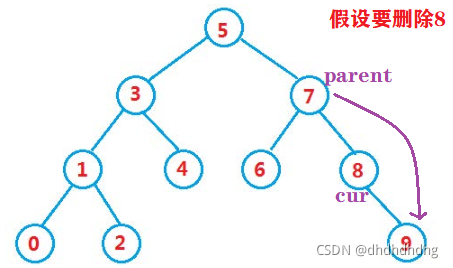
一般情况:
cur是parent的左子树:parent.left=cur.right
cur是parent的右子树:parent.right=cur.right
注意将cur.right置为null
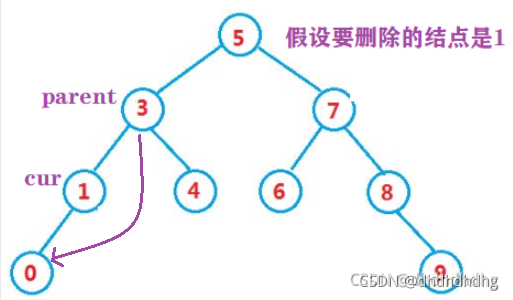
②只有左子树:
与右子树思路一致,这里不作过多解释
③左子树和右子树都有:
这里就不能直接删除,因为指向左或者右都不可以
需要使用替换法进行删除,即:1.寻找一个替代结点 (左子树中最大的或者右子树中最小的,一般情况下都是在右子树中找的)
2.将替代结点的值交给待删除结点
3.将替代结点删除掉
代码实现:
public boolean remove(int key){
//查找待删除结点所在位置
Node cur=root;
Node parent=null;
while(cur!=null){
if(key==cur.key){
break;
}else if(key<cur.key){
parent=cur;
cur=cur.left;
}else{
parent=cur;
cur=cur.right;
}
}
//该元素不在二叉搜索树中
if(cur==null){
return false;
}
//叶子节点或者只有右子树
if(cur.left==null){
if(parent==null){
//cur是根节点
root=cur.right;
}else{
if(parent.left==cur){
parent.left=cur.right;
}else if(parent.right==cur){
parent.right=cur.right;
}
}
cur.right=null;
//只有左子树
}else if(cur.right==null){
if(parent==null){
//cur是根节点
root=cur.left;
}else {
if (parent.left == cur) {
parent.left = cur.left;
} else if (parent.right == cur) {
parent.right = cur.left;
}
}
cur.left = null;
}else{
//左子树和右子树都不为空
//在子树中找替代节点,左子树中最大的或者右子树中最小的
//一般情况下都是在右子树中找的
Node delNode=cur.right;
//找到替代结点
parent=cur;
while(delNode.left!=null){
parent=delNode;
delNode=delNode.left;
}
//替换
cur.key=delNode.key;
//删除替代结点
if(parent.left==delNode){
parent.left=delNode.right;
}else{
parent.right=delNode.right;
}
delNode.right=null;
}
return true;
}
}