[数据结构与算法] 数据结构总结6 树

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据结构总结6 树 -> 正文阅读

[数据结构与算法]数据结构总结6 树

小技巧速记

非空二叉树的第 i 层上最多有 $2^{i-1}$ 个结点（i ≥ 1）
一棵深度为 k 的二叉树中，最多具有 $2^{k}-1$ 个结点
对于一棵非空的二叉树，如果叶子结点数为 n₀，度数为2的结点数为 n₂，则有 n₀ = n₂＋1
具有 n 个结点的完全二叉树的深度 k 为 $log_{2}n] + 1$
完全二叉树以从上至下和从左到右的顺序对二叉树中所有结点从 1 开始顺序编号，元素编号序列为 { 1, 2, …, i, …, n }，则
（1）若根结点为i，则 左子树为2i，右子树为2i+1，双亲结点为i/2
（2）结点为i，若 2i > n 无左子树，若2i+1 > n 无右子树
已知完全二叉树的叶子个数为 n₀，最少具有的结点数为 $2n_{0}-1$ ，最多节点数为 $2n_{0}$

基础知识

结点的度：分支的个数（子树的个数）
树的度：树中所有结点的度的最大值
叶子：度为 0，没有左右子树
结点的层次：若根节点的层次为1，第 i 层的结点的子树根结点的层次为 i+1
树的深度：叶子结点所在的最大层次
有序树：左右子树不能任意互换的树
森林：若干棵不相交的树的集合
完全二叉树：树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应
如果存在一棵二叉树，对树中的结点自上而下、自左而右连续编号，若编号为i的结点与满二叉树中编号为i的结点的位置相同，则称此二叉树为完全二叉树

练习题

在下列三种次序的线索二叉树中，对查找指定结点在该次序下的后继效果较差的一种是（）
A. 前序线索树
B. 中序线索树
C. 后序线索树
解析：先序最先访问的是根节点；中序最先访问的是最左下；后序最先访问的情况比上面的复杂，后续的寻找也复杂
如图所示的t2是由有序树t1转化而来的二叉树，那么树t1有 ___ 个叶结点

答案：6
解析：（一种解释?）左孩子右兄弟的树t2 还原成树间不相连的森林t1后，共有6个叶子结点
将图中的二叉树按中序线索化，结点 X 的右指针和 Y 的左指针分别指向（）

答案：D、A
解析?：中序线索序列：C B A Y X D E，X右为D，Y左为A
已知某二叉树的后序遍历是d a b e c ，中序遍历序列是d e b a c，它的前序遍历序列是（）
A. acbed
B. decab
C. deabc
D. cedba
解析：如果是一个平衡二叉树（左右子树分配比较均匀），则在中序遍历中，从左下向右上扫描，序列中的第一个元素为树结构中的最左下结点，树根应该出现在序列的中间；在后序遍历中，从下向上扫描，序列中的第一个元素为树结构中的最下左结点，树根应该出现在序列的最后；本题中，现根据后序遍历确定树根为c，再根据中序序列分隔出左右子树序列，c的左子树为deba，右子树为空；再递归分析出左子树的树根为e，再分隔左子树的左右子树…，最后得到的树结构为：^{(层次遍历：层数-双亲-左右)}{¹[c], ^2-c-l[e],^3-e[d, b],^4-b-r[a]}
设n,m为一棵树上的两个结点，在中序遍历时，n在m前的条件是（）
A. n在m右方
B. n是m祖先
C. n在m左方
D. n是m子孙
在一非空二叉树的中序遍历序列中，根结点的右边（）
A. 只有右子树上的所有结点
B. 只有右子树上的部分结点
C. 只有左子树上的部分结点
D. 只有左子树上的所有结点
用顺序存储的方法将完全二叉树中所有结点逐层存放在数组R[1…n]中，结点R[i]若有左子树，则左子树是结点（）
A. R[2i+1]
B. R[2i]
C. R[i/2]
D. R[2i -1]
假定在一棵二叉树中，双分支结点数为15，单分支结点数为30个，则叶子结点数为（）
A. 15
B. 16
C. 17
D. 47
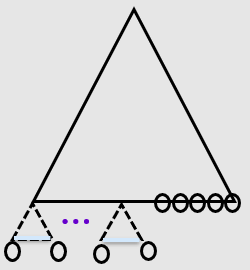
解析：二叉树性质3（非空二叉树的叶子结点数为 n₀，度数为2的结点数为 n₂，则有 n₀ = n₂＋1）
含有129个叶结点的完全二叉树，最少有（）个结点
A. 255
B. 256
C. 257
D. 258
解析：n₀*2-1为完全二叉树最少具有的结点数；证明：n₁=0时候最少，故n=n₂+n₀=2n₀-1
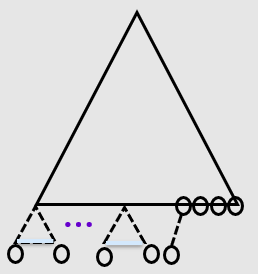
一棵有124个叶结点的完全二叉树，最多有（）个结点
A. 247
B. 248
C. 249
D. 250
解析：n₀*2为完全二叉树最多具有的结点数；证：n₁=1的时候是最多，故n=n₀+n₁+n₂=2n₀
假设根结点的层数为0，在一棵二叉树上第5层的结点数最多为（ 2⁵ ）
设高度为h的二叉树中只有度为0和度为2 的结点，则此类二叉树中所包含的结点数至多为（），至少为（）
答案：2^h - 1、2h - 1
对一个满二叉树，m个树叶，n个结点，深度为h，则（）
A. n = h + m
B. h + m = 2n
C. m = h -1
D. n = 2^h – 1
按照二叉树的定义，具有3个结点的二叉树有 ___ 种形态
答案：5
对二叉树的结点从1开始连续编号，要求每个结点的编号大于其左，右孩子的编号，同一结点的左，右孩子中，其左孩子编号小于其右孩子编号，则可采用（）次序的遍历实现二叉树的结点编号
A. 先序
B. 中序
C. 后序
D. 从根开始按层次遍历
树最合适用来表示（）
A. 有序数据元素
B. 元素之间具有分支层次关系的数据
C. 无序数据元素
D. 元素之间无联系的数据
线性结构和非线性结构都可以用顺序结构存储（ √ ）
在后序线索二叉树中，若某结点p且p->rtag=1，则后续遍历时候，p的直接后继是p->rchild （ √ ）
满二叉树每个分支都有两棵高度相同的子树（ √ ）
满二叉树的叶子结点都在最底层，不存在 1 度结点（ √ ）
高度相同的二叉树中，满二叉树拥有最多的结点（ √ ）
在线索二叉树中，只知道某节点地址p，可以找到中序前驱和后继，前序后继，后续前驱，找不到前序前驱，后序后继

6.1 二叉树

二叉树的性质

非空二叉树的第 i 层上最多有 $2^{i-1}$ 个结点（i ≥ 1）
一棵深度为 k 的二叉树中，最多具有 $2^{k}-1$ 个结点
对于一棵非空的二叉树，如果叶子结点数为 n₀，度数为2的结点数为 n₂，则有 n₀ = n₂＋1
具有 n 个结点的完全二叉树的深度 k 为 $log_{2}n] + 1$
完全二叉树以从上至下和从左到右的顺序对二叉树中所有结点从 1 开始顺序编号，元素编号序列为 { 1, 2, …, i, …, n }，则
（1）若根结点为i，则 左子树为2i，右子树为2i+1，双亲结点为i/2
（2）结点为i，若 2i > n 无左子树，若2i+1 > n 无右子树

二叉树的存储结构

二叉树的顺序存储表示（数组）：
二叉树的链式存储表示

结点结构：

lchild	data	rchild

代码实现：

typedef struct BiTNode {
	ElemType data;
	struct BiTNode* lchild;
	struct BiTNode* rchild;
}BiTNode, *BiTree;

三叉链表

parent	lchild	data	rchild

双亲链表

data	parent	LRTag

typedef struct BPTNode {
	ElemType data;
	int* parent;  //指向根的指针
	char LRTag;  //左、右子树标志
}BiTNode;
typedef struct BPTree {
	BPTNode nodes[SIZE];
	int num_node;  //结点数目
	int root;  //根结点位置
}BPTree;

二叉树的遍历

先序 / 中序 / 后序遍历（递归）

先(根)序遍历：
（1）访问 根结点
（2）先序遍历左子树
（3）先序遍历右子树

void PreOrder(BiTree T, void(*visit)(ElemType& e)) {
	if(!T) return;
	visit(T->data); //访问根节点
	PreOrder(T->lchild, visit);  //先序遍历左子树
	PreOrder(T->rchild, visit);  //先序遍历右子树
}

中(根)序遍历：
（1）中序遍历左子树
（2）访问 根结点
（3）中序遍历右子树

void InOrder(BiTree T, void(*visit)(ElemType& e)) {
	if(!T) return;
	InOrder(T->lchild, visit);  //中序遍历左子树
	visit(T->data); //访问根节点
	InOrder(T->rchild, visit);  //中序遍历右子树
}

后(根)序遍历：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问 根结点

void PostOrder(BiTree T, void(*visit)(ElemType& e)) {
	if(!T) return;
	PostOrder(T->lchild, visit);  //后序遍历左子树
	PostOrder(T->rchild, visit);  //后序遍历右子树
	visit(T->data); //访问根节点
}

层次遍历

void LevelTraverse(BiTree T) { //层次遍历
	if(!T) return;
	int front = -1, rear = 0;
	BiTree Queue[100];
	Queue[rear] = T;  // 树根入队
	while(front != rear) {
		cout << Queue[++front]->data << " ";  //访问队首结点 
		if(Queue[front]->lchild != NULL)  //队首结点的左子树入队 
			Queue[++rear] = Queue[front]->lchild;
		if(Queue[front]->rchild != NULL)  //队首结点的右子树入队 
			Queue[++rear] = Queue[front]->rchild;
	}	
}

先序 / 中序 / 后续遍历（迭代）

非递归中序遍历：

BiTNode *GoFarLeft(BiTree T,stack<BiTNode *> &S) //找T的最左下结点
{
    if(!T) return NULL;
    while(T->lchild)
    {
        S.push(T);
        T=T->lchild;
    }
    return T;
}
void Inorder_I(BiTree T) //非递归的中序遍历
{
    /**请完善该函数，需要用到的GoFarLeft函数上面已经定义完毕**/
	stack<BiTree> S;
	T = GoFarLeft(T, S);
	while (T) 
	{
		cout << T->data;
		if(T->rchild)
			T = GoFarLeft(T->rchild, S);
		else if(!S.empty()) {
			T = S.top();  //访问跟节点
			S.pop(); 
		}
		else T = NULL;
	}
}

树的叶子数和深度

void CountLeaf(BiTree T,int &c) //计算叶子节点数量
{
	if(!T) return;  //空树 
	if(!T->lchild && !T->rchild) //没有左右子树 是叶子节点 
		c++;
	CountLeaf(T->lchild, c);
	CountLeaf(T->rchild, c);
}

int Depth(BiTree T) //计算二叉树的深度
{
	if(!T) return 0;
	int ldepth = Depth(T->lchild);
	int rdepth = Depth(T->rchild);
	return 1 + (ldepth>rdepth ? ldepth : rdepth); 
}

6.2 线索二叉树

typedef enum { Link, Thread } Tag;
//Link:指针, Thread:线索
typedef struct BiThrNode{ //线索二叉树结点结构
    string data;
    struct BiThrNode *lchild,*rchild;  //左右指针(根据标志指向不同)
    bool LTag, RTag; //左右线索标志
} BiThrNode, *BiThrTree;

BiThrTree pre;                //全局变量
//中序线索化以p为根的树
void InThreading(BiThrTree p) {
    if (!p) return;
	InThreading(p->lchild);
    if (!p->lchild) {  //建前驱线索
        p->LTag = Thread;  //Thread = 1
        p->lchild = pre;
    }
    if (!pre->rchild) {  //建后驱线索
        pre->RTag = Thread;  //Thread = 1
        pre->rchild = p;
    }
    pre = p;  //保持 pre 指向 p 的前驱
    InThreading(p->rchild);
}
//构建中序线索链表
bool InOrderThreading(BiThrTree &Thrt, BiThrTree T) {
    Thrt = new BiThrNode;  //构建头结点
    Thrt->LTag = Link;  //Link = 0
    Thrt->RTag = Thread;  //Thread = 1
    Thrt->rchild = Thrt;  //添加头节点

    if (!T)
        Thrt->lchild = Thrt; //如果T是空树
    else {
        Thrt->lchild = T; //为初始化Thrd的左子树指向真正的树根，Thrd为增加的头结点
        pre = Thrt;

        InThreading(T);

        pre->rchild = Thrt; // 处理最后一个结点,此时Thrd为根，pre 为最后一个结点
        pre->RTag = 1;
        Thrt->rchild = pre;
    }
    return true;
}
//中序线索化链表的遍历
void InOrderTraverse_Thr(BiThrTree T)
{
    BiThrTree p = T->lchild;
    while (p != T) { // 空树或遍历结束时，p==T
        while (p->LTag == 0)
            p = p->lchild;  //找到最左下结点
        cout << p->data;
        while (p->RTag == 1 && p->rchild != T) { //访问后继节点
            p = p->rchild;
            cout << p->data;
        }
        p = p->rchild;  //进入右子树根
    }  // 空树/遍历结束 p == T
}

6.3 树和森林

树和森林的表示

双亲表示法

结点结构 |data|parent|
typedef struct PTNode {
	ElemType data;
	int parent;  //双亲位置
} PTNode;

树结构
typedef struct PTree {
	PTNode nodes[MAXSIZE];
	int root;  //根节点位置
	int number;  //结点个数
} PTree;

孩子链表

孩子结点结构 |child|next|
typedef struct CTNode {
	ElemType data;
	int parent;  //双亲位置
} *ChildPtr;

双亲结点结构 |data|firstchild|
typedef struct PTree {
	ElemType data;
	ChildPtr firstchild;  //孩子链表的头指针
} CTBox;

树结构
typedef struct PTree {
	CTBox nodes[MAXSIZE];
	int root;  //根节点位置
	int number;  //结点个数
} CTree;

左孩子右兄弟

结点结构 |firstchild|data|nextsibling|
typedef struct CSNode {
	ElemType data;
	struct CSNode* firstchild;
	struct CSNode* nextsibling;
} CSNode, *CSTree;

树和森林的遍历

树的遍历和二叉树遍历的对应关系

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后根遍历	中序遍历	中序遍历

6.4 哈夫曼树哈夫曼编码

结点的路径长度：从根节点到该结点的路径上分支的数目
树的路径长度：树中每个结点的路径长度之和
树的带权路径长度：树中所有叶子结点的带权路径长度之和
最优树：在所有含n个叶子结点、并带有相同权值的m叉树种，必存在一颗其带权路径长度取最小值的树
哈夫曼树：最小带权路径长度的二叉树
特点：具有 n 个叶子结点的哈夫曼树共有 2n-1 个结点

构造哈夫曼树（最优树）

根据给定的 n 个权值 {w₁, w₂, …, w_n}，构造 n 棵二叉树的集合F = {T₁, T₂, … , T_n}，其中每棵二叉树中均只含一个带权值为 w_i 的根结点，其左、右子树为空树
在 F 中选取其根结点的权值为最小的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和
从F中删去这两棵树，同时加入刚生成的新树
重复 2. 和 3. 两步，直至 F 中只含一棵树为止

注意：在合并中不是选取根结点权值最小的两棵二叉树（包括已合并的和未合并的），而是选取未合并的根结点权值最小的一棵二叉树与已经合并的二叉树合并