常见排序及分类
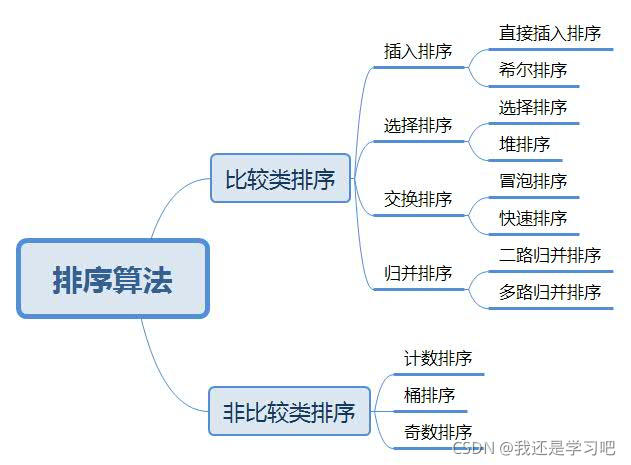
这里暂时先只总结
- 直接插入排序
- 希尔排序
- 选择排序
- 堆排序
- 冒泡排序
- 快速排序
- 二路归并排序
- 计数排序
直接插入排序
动图演示:
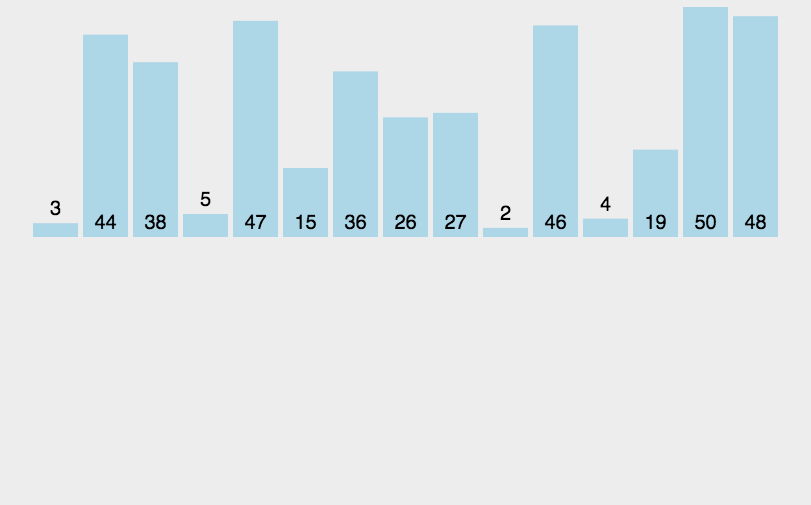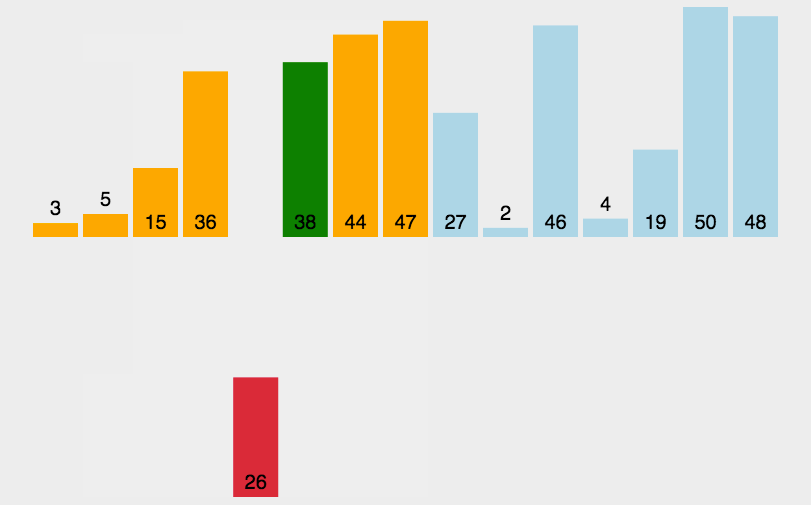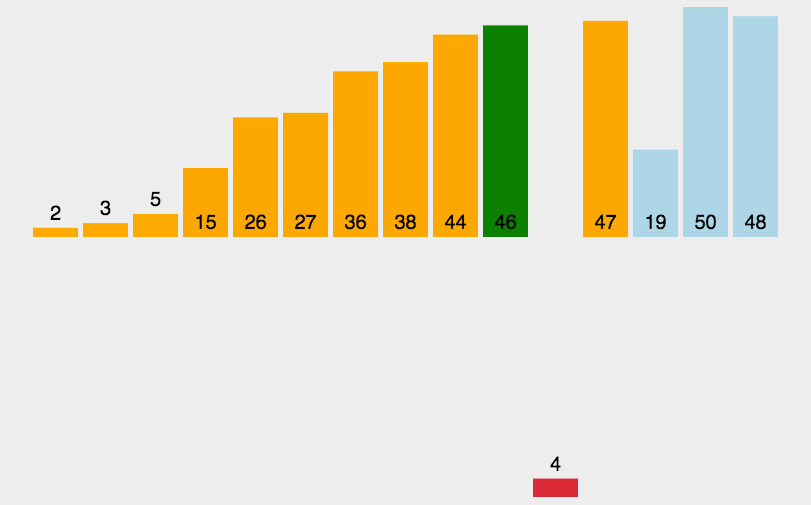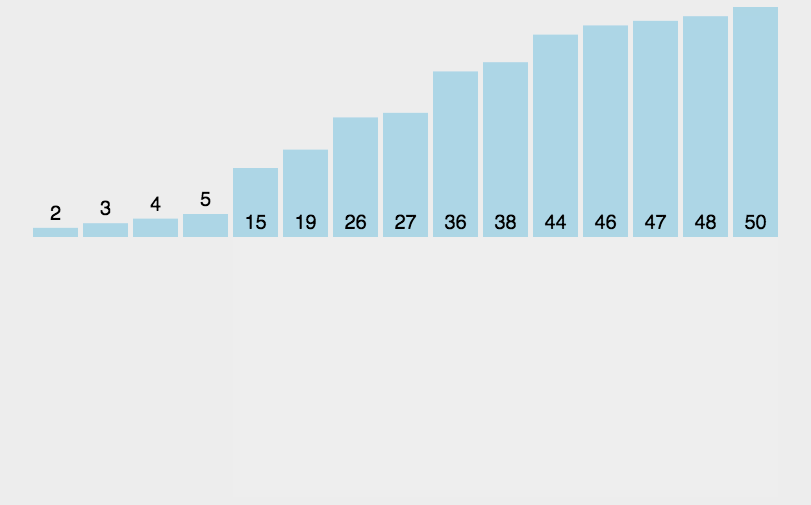
分析:

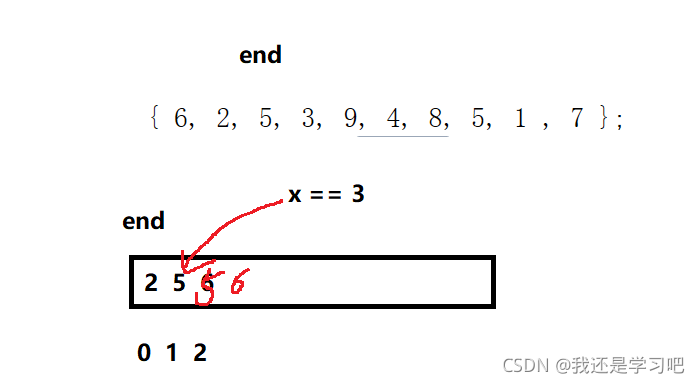
直接插入最坏为O(N^2)
最好可以达到O(N)
void InserSort(int* a, int n)
{
for(int i = 0; i < n - 1; ++i)
{
int end = i;
int x = a[end+1];
while(end >= 0 )
{
if(a[end] > x)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = x;
}
}
希尔排序
动图演示:
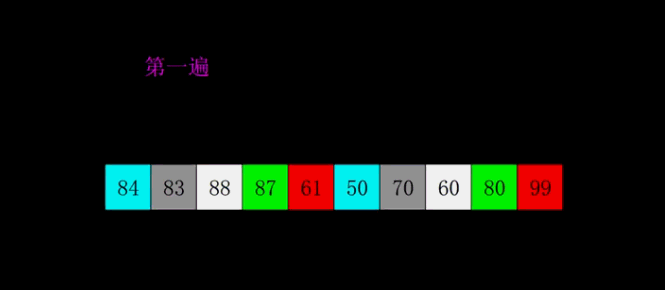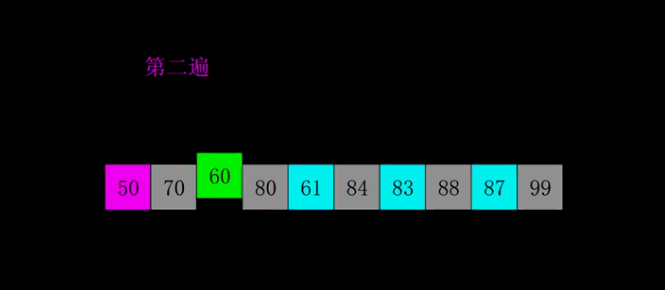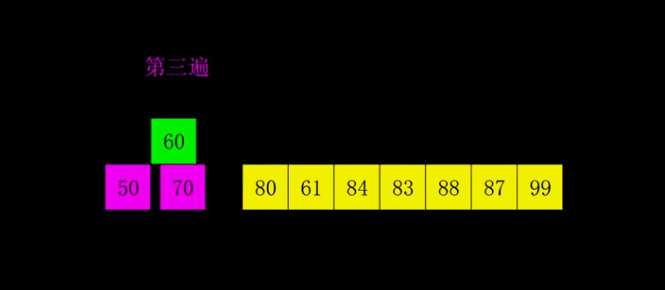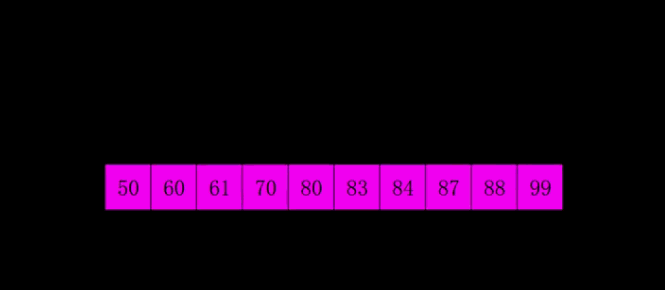
分析:

希尔排序的优势需要在数据量大时才体现得明显。
先写一趟的代码用于理解
//假设gap==3
int gap = 3;
for(int j = 0; j < gap; ++j)
{
for(int i = j; i < n - gap; i += gap)
{
int end = i;
int x = a[end + gap];
while(end >= 0)
{
if(a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
void ShellSort(int* a, int n)
{
int gap = n;
while(gap > 1)
{
//gap = gap / 2;//这是另一种写法,每次除2可以保证最后一次一定是1
gap = gap / 3 + 1;//+1是为了保证对任何数量的数据最后一次gap都能等于1
//同时归并多组(交替着进行多组的插入排序
for(int i = 0; i < n - gap; ++i)
{
int end = i;
int x = a[end + gap];
while(end >= 0)
{
if(a[end] > x)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
}
选择排序
动图演示:
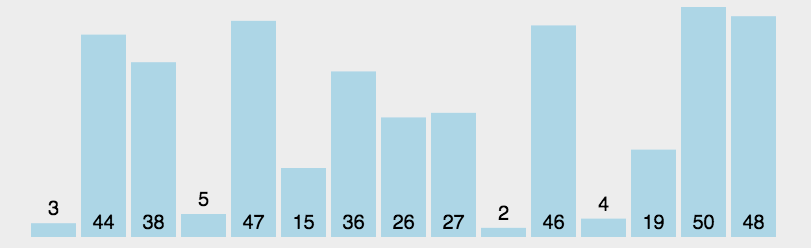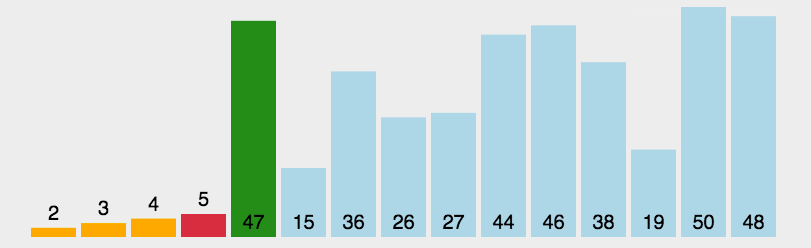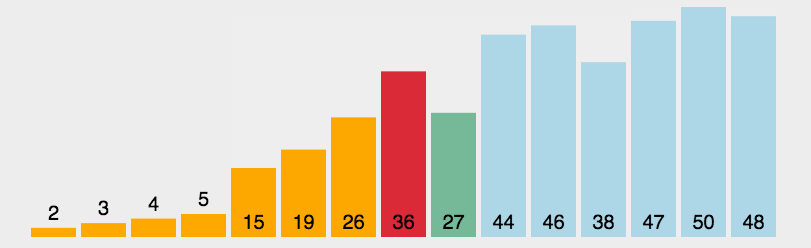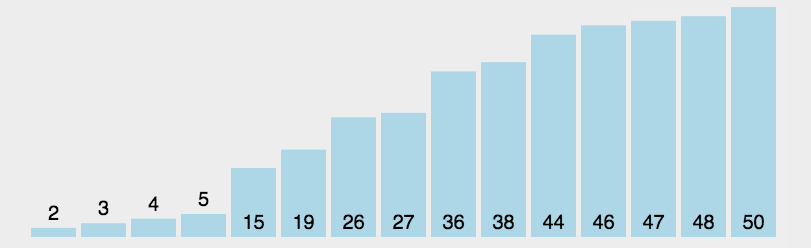
分析:

void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void SelectSort(int* a, int n)
{
//begin和end控制每次遍历数组的边界
int begin = 0, end = n - 1;
while(begin < end)
{
//给一个初始值
int mini = begin, maxi = begin;
for(int i = begin; i <= end; ++i)
{
if(a[i] < a[mini])
{
mini = i;
}
if(a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[mini], &a[begin]);
if(begin == maxi)
{
maxi = mini;
}
Swap(&a[maxi], &a[end]);
++begin;
--end;
}
}
堆排序
动图演示:

分析:
关于向下调整建堆和向上调整建堆在顺序存储的二叉树文章中总结了。
需要注意向上调整建堆的时间复杂度为O(N*logN);
而使用向下调整建堆时间复杂度为O(N)

//一次向下调整
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while(child < n)
{
//建大堆,选出大孩子
if(child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if(a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;//每次向下调整到叶子结点结束
}
else
{
break;//或者父亲结点大于两个孩子结点结束
}
}
}
//堆排序
void HeapSort(int* a, int n)
{
//先建堆
//向下调整建堆的方法是从第一个非叶子结点开始,到根节点,依次向下调整
//所以i最后一次等于0
for(int i = (n - 1 - 1) / 2 - 1; i >= 0; --i)
{
//向下调整需要直到n是为了确定是否向下调整到了叶子结点
//(叶子结点没有孩子)
AdjustDown(a, n, i);
}
int end = n - 1;
while(end > 0)
{
Swap(&a[0], &a[end]);//把最大值拿到最后
AdjustDown(a, end, 0);//不把放到后面的数看作堆里的数,对根向下调整
--end;
}
}
冒泡排序
动图演示:
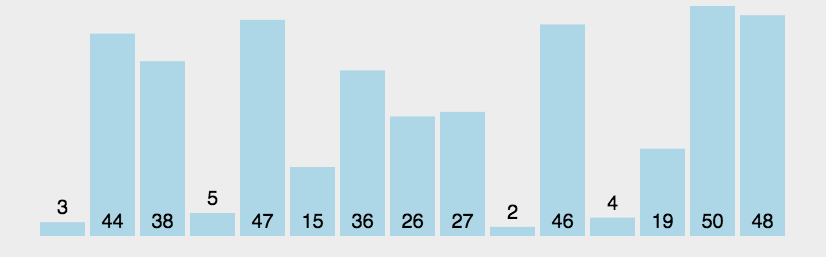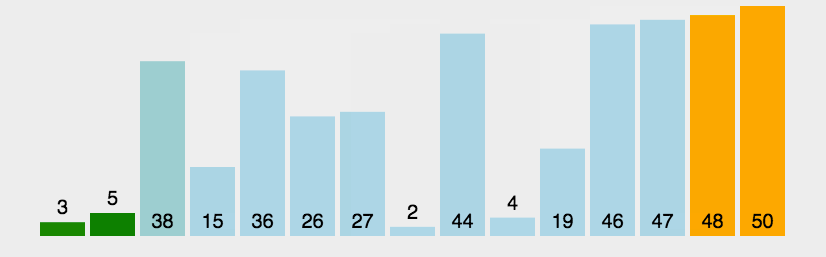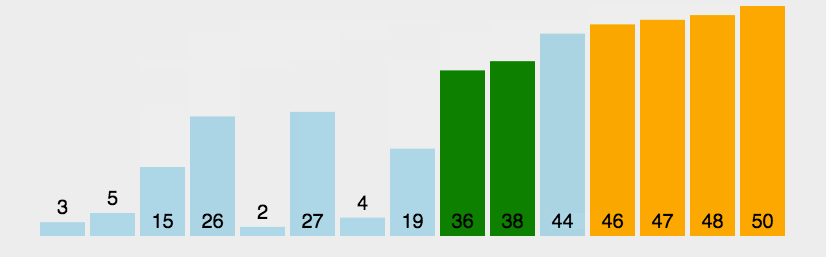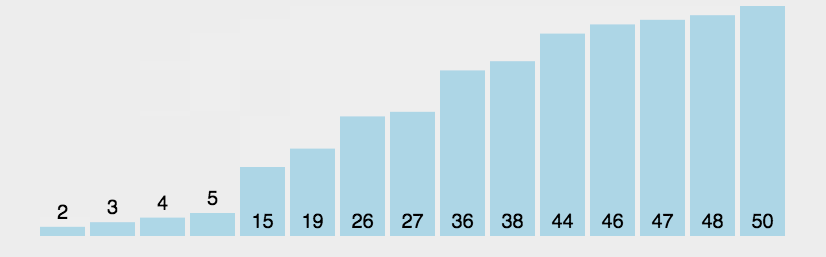
分析:


void BubleSort(int* a, int n)
{
int end = n;
while(end > 1)
{
int exchange = 0;
for(int i = 1; i < end; ++i)
{
if(a[i - 1] > a[i];
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
--end;
if(exchange == 0)
{
break;
}
}
}
用for循环写就是
void BubbleSort(int* a, int n)
{
for(int j = 0; i < n - 1; ++j)
{
for(int i = 1; i < n - j; ++i)
{
if(a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
}
}
}
}
快速排序
先写单趟处理
快速排序单趟排序有多种写法,这里整理三种
1.Tony Hoare版本(快排发明者最初的写法)
动图演示:
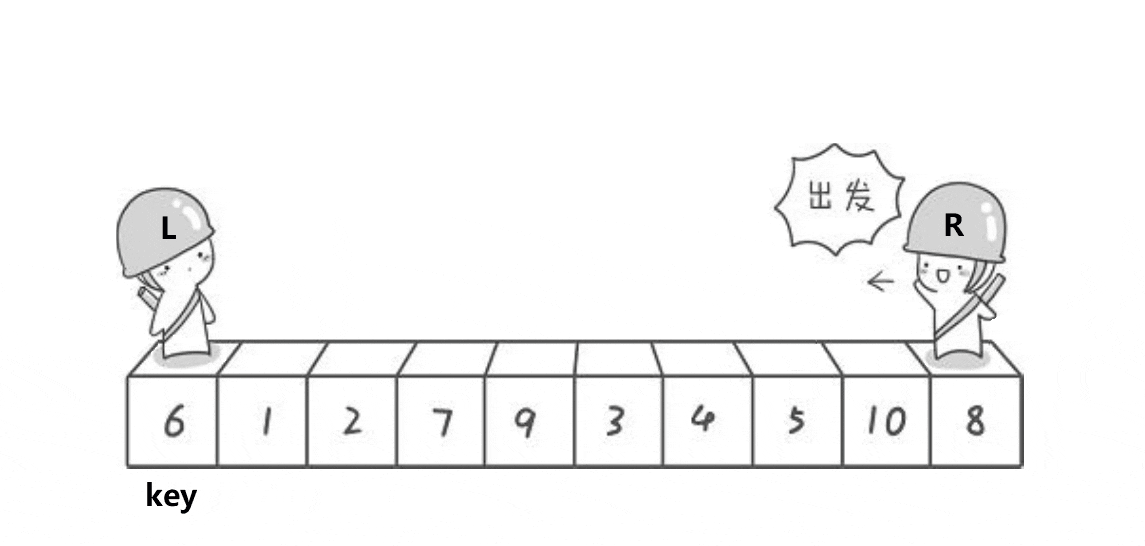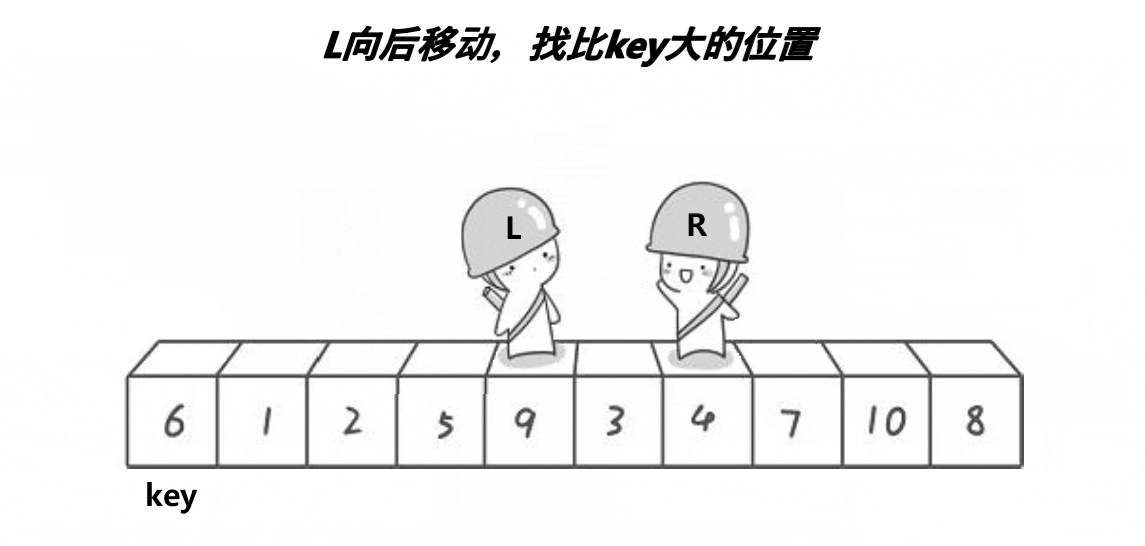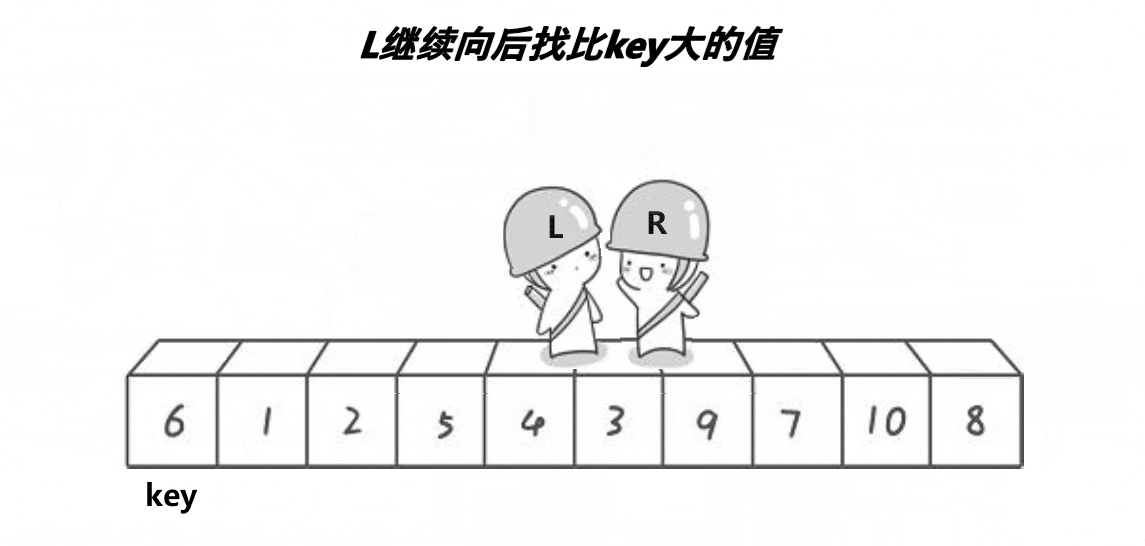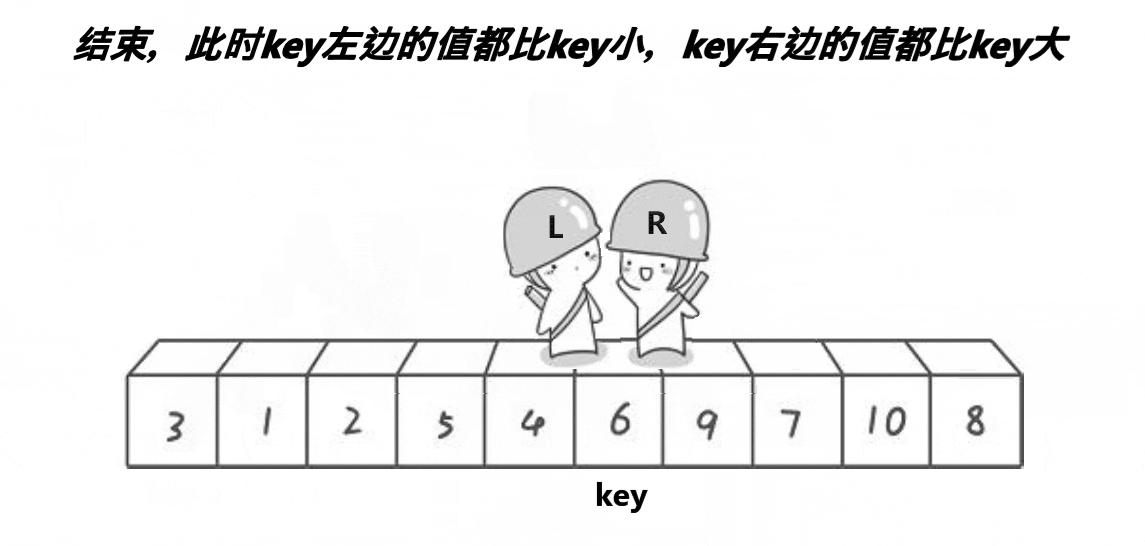
分析:

int PartSort1(int* a, int left, int right)
{
//左边作key
int keyi = left;
while(left < right)
{
//右边先走,找小
while(left < right && a[right] >= a[keyi])
{
-- right;
}
//左边再走,找大
while(left < right && a[left] <= a[keyi])
{
++right;
}
Swap(&a[left], &a[right]);
}
//相遇位置和keyi交换
Swap(&a[left], &a[keyi]);
//返回相遇位置
return left;
}
三数取中
int GetMidIndex(int* a, int left, int right)
{
int mid = left + ((right - left) >> 1);
if(a[left] < a[mid])
{
if(a[mid] < a[right])
{
return mid;
}
else if(a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else//a[left] > a[mid]
{
if(a[mid] > a[right])
{
return mid;
}
else if(a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
则单趟排序需要修改为
int PartSort(int* a, int left, int right)
{
int mid = GetMidIndex(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
while(left < right)
{
//右边先走,找小
while(left < right && a[right] >= a[keyi])
{
--right;
}
while(left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}
再看如何把整个数组排成有序
分析:
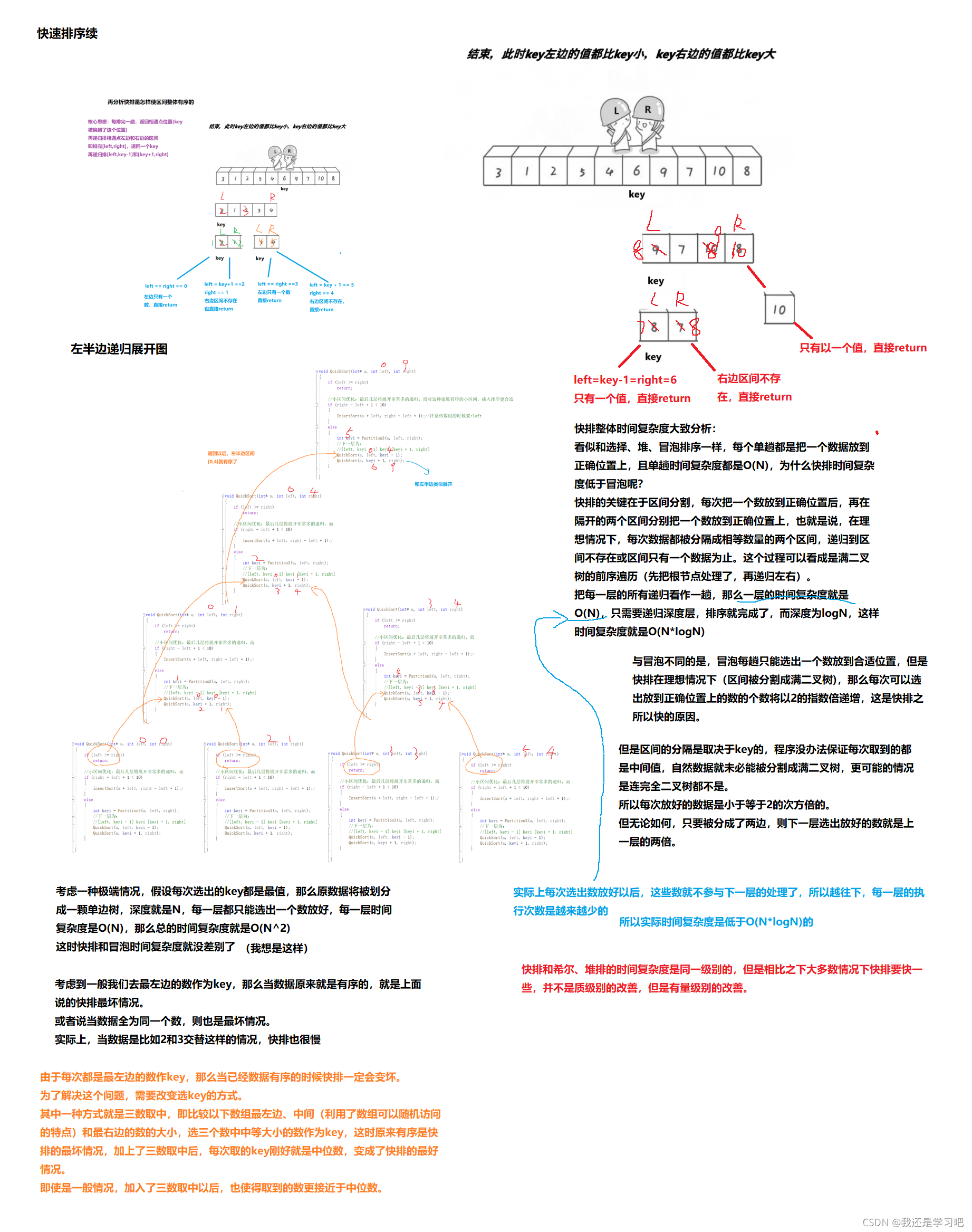
快排代码为:
void QuickSort(int* a, int left, int right)
{
//递归结束条件
if(left >= right)
return;
int keyi = PartSort(a, left, right);
//下一层为[left,keyi-1] [keyi+1,right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
单趟排序第二种写法:挖坑法
动图演示:
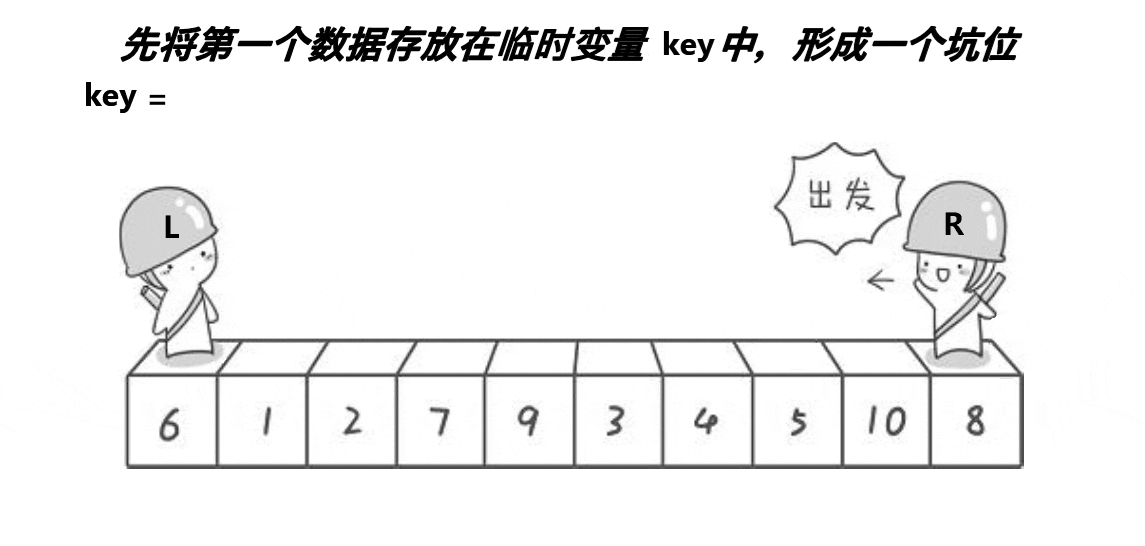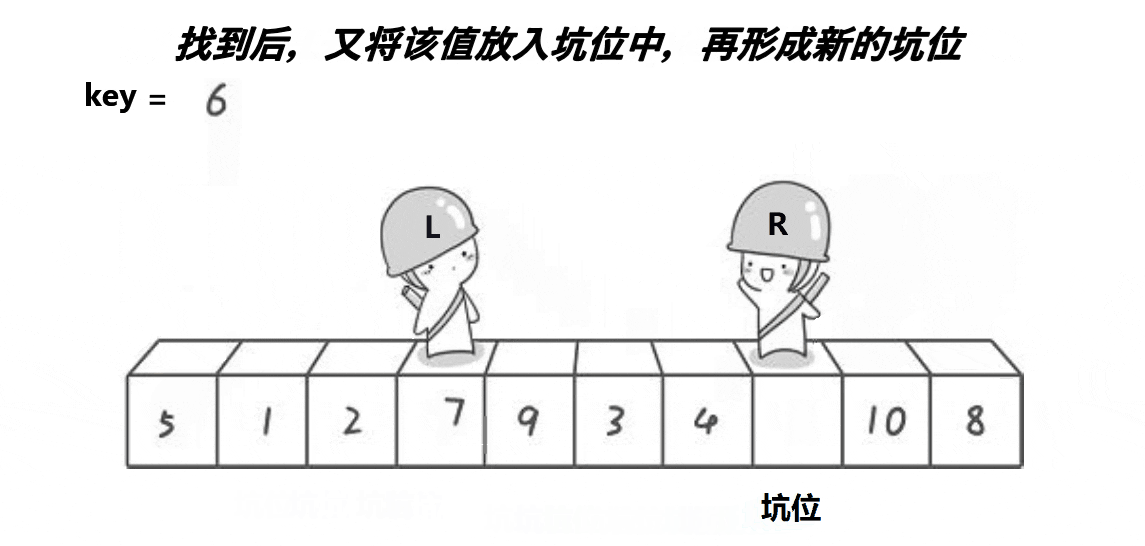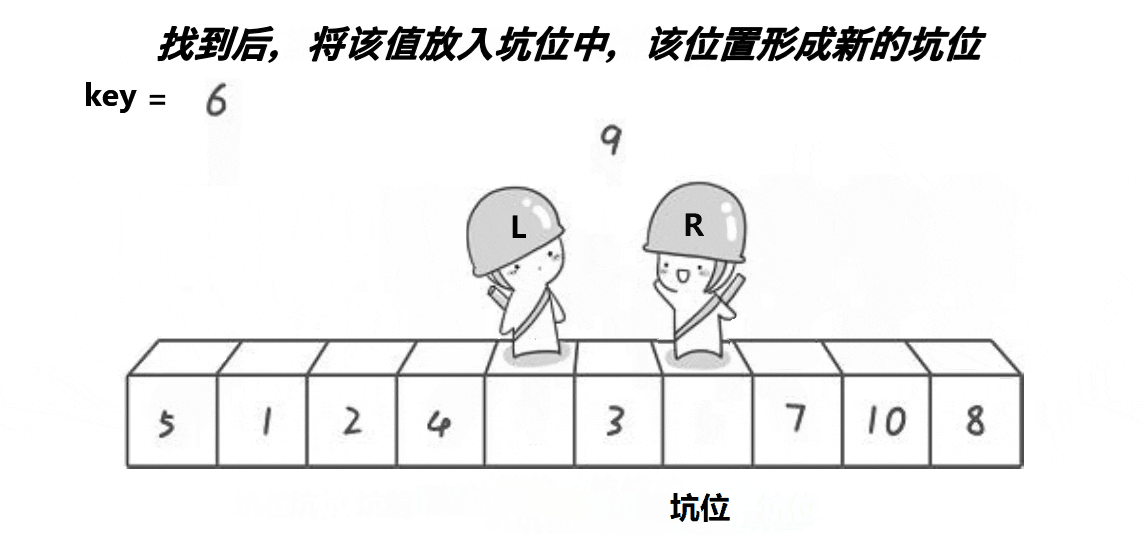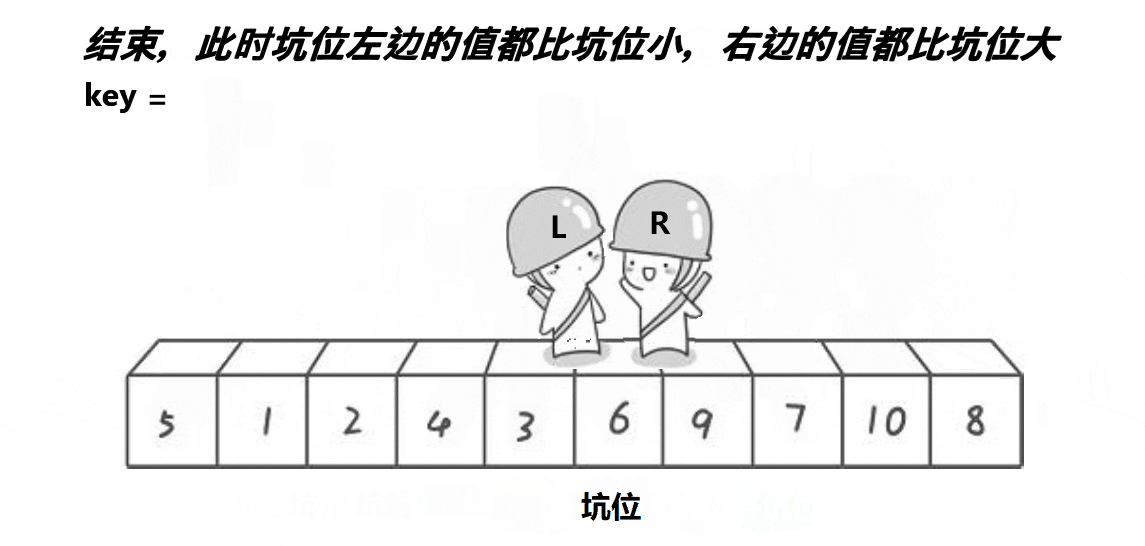
分析:

int PartSort2(int* a, int left, int right)
{
int mid = GetMidIndex(a, left, right);
Swap(&a[left], &a[mid]);
int key = a[left];
int pit = left;
while(left < right)
{
//右边找小,放到左边的坑里
while(left < right && a[right] >= key)
{
--right;
}
a[pit] = a[right];
pit = right;
//左边找大,放到右边的坑里
while(left < right && a[left] <= key)
{
++left;
}
a[pit] = a[left];
pit = left;
}
a[pit] = key;
return pit;
}
快排单趟第三种写法:前后指针法
动图演示:
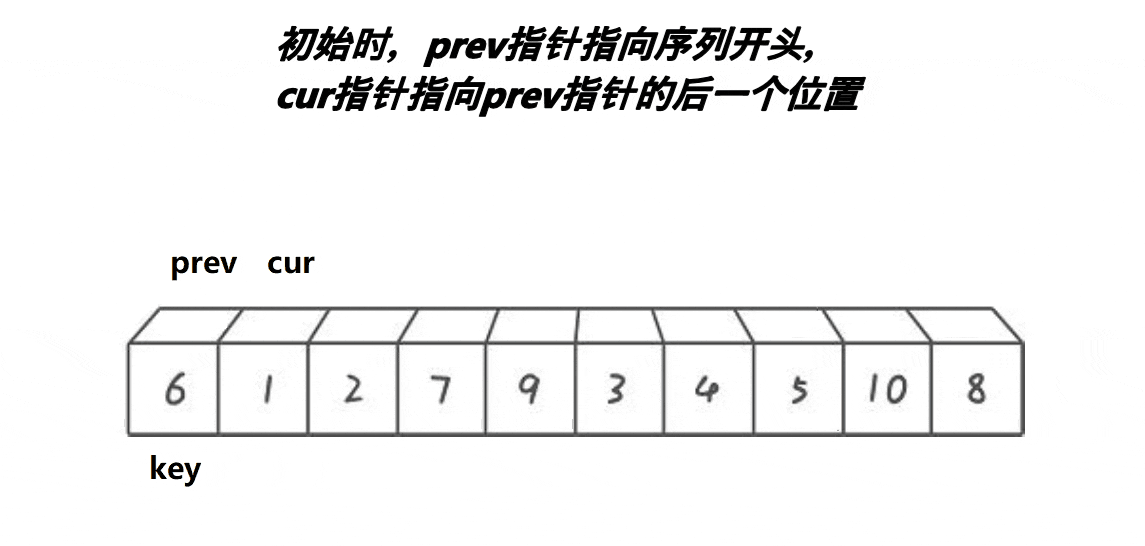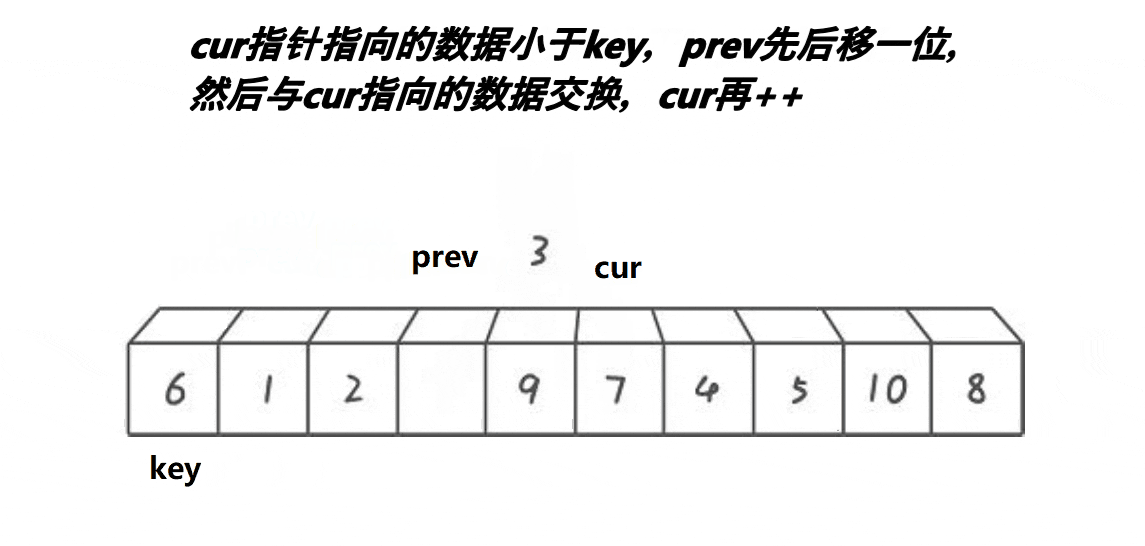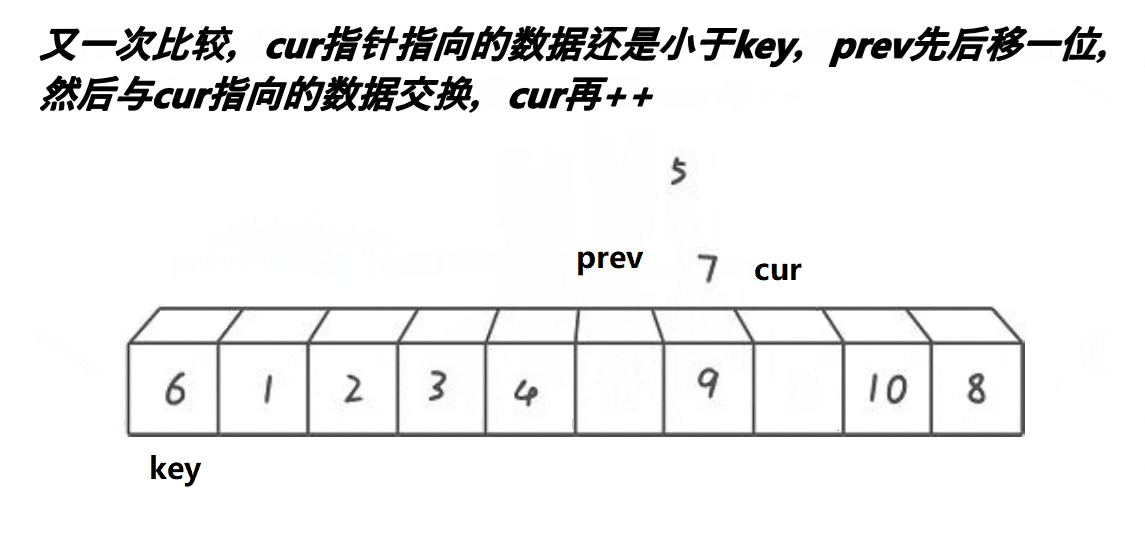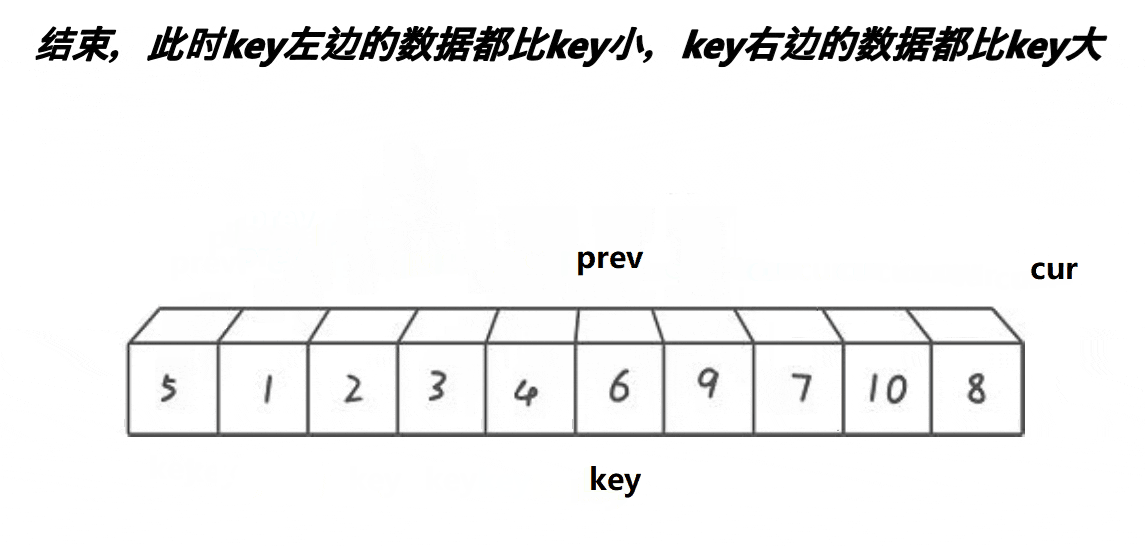
分析:

int PartSort3(int* a, int left, int right)
{
int mid = GetMidIndex(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
int prev = left;
int cur = prev + 1;
while(cur <= right)
{
while(cur <= right && a[cur] >= a[keyi])
{
++cur;
}
if(cur <= right)
{
Swap(&a[cur], &a[++prev]);
++cur;
}
}
Swap(&a[prev], &a[keyi]);
return prev;
}
简洁写法
int PartSort3(int* a, int left, int right)
{
int mid = GetMidIndex(a, left, right);
Swap(&a[left], &a[mid]);
int keyi = left;
int prev = left;
int cur = prev + 1;
while(cur <= right)
{
if(a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
快排的小区间优化

void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
//小区间优化:最后几层将展开非常多的递归,而对这种接近有序的小区间,插入排序更合适
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);//注意传数组的时候要+left
}
else
{
int keyi = Partition3(a, left, right);
//下一层为:
//[left, keyi - 1] keyi [keyi + 1, right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
}
快排非递归写法
分析:
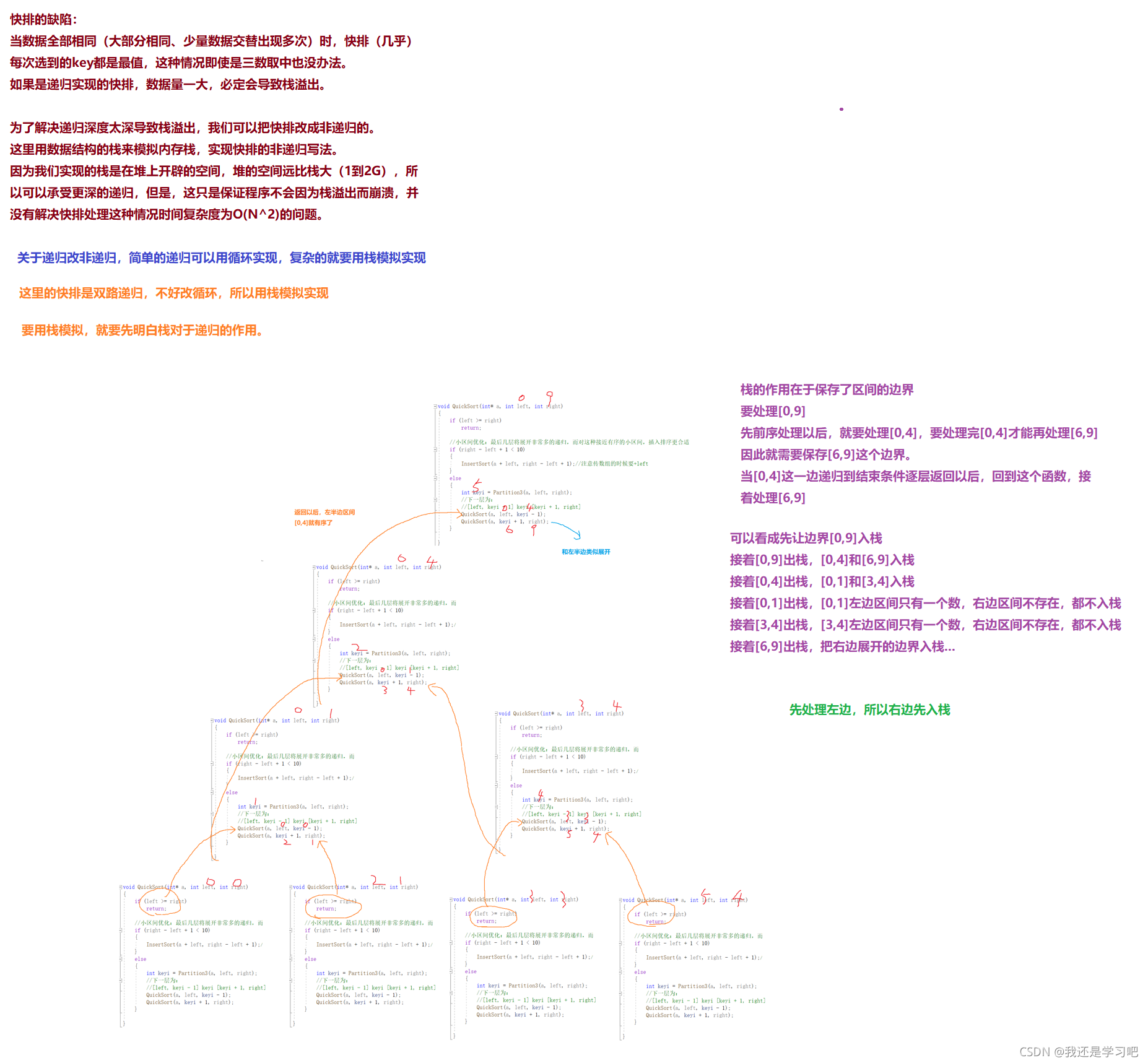
void QuickSort(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while(!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int keyi = PartSort3(a, begin, end);
//如果右区间还有值,右边先入栈
if(keyi + 1 < end)
{
StackPush(&st, keyi + 1);
StackPush(&st, end);
}
//如果左区间还有值,左区间后入栈
if(begin < keyi - 1)
{
StackPush(&st, begin);
StackPush(&st, keyi - 1);
}
}
//栈为空时,所有区间都处理过了,就有序了
StackDestroy(&st);
}
归并排序
动图演示:
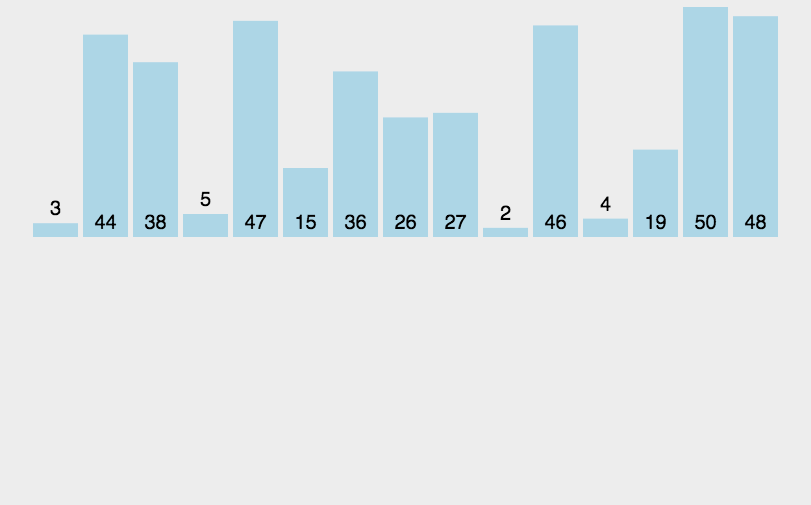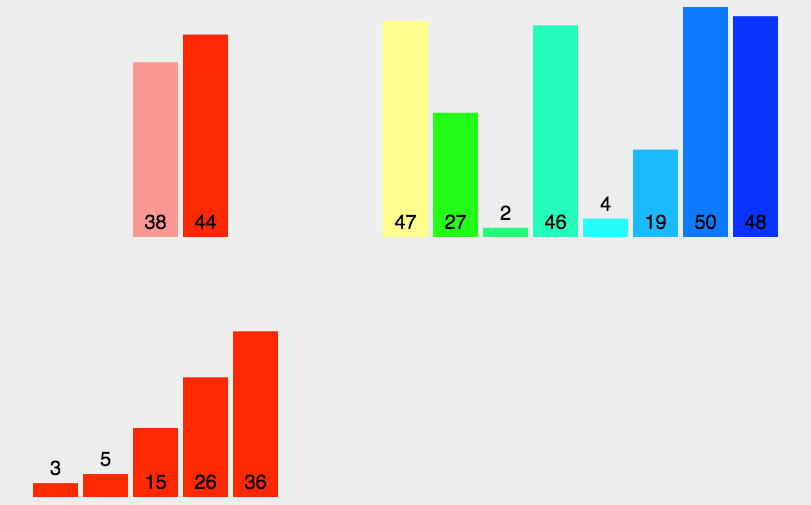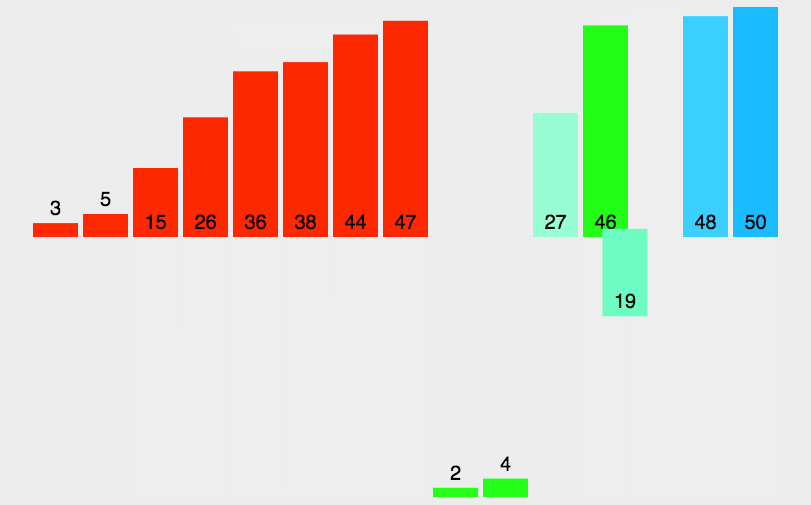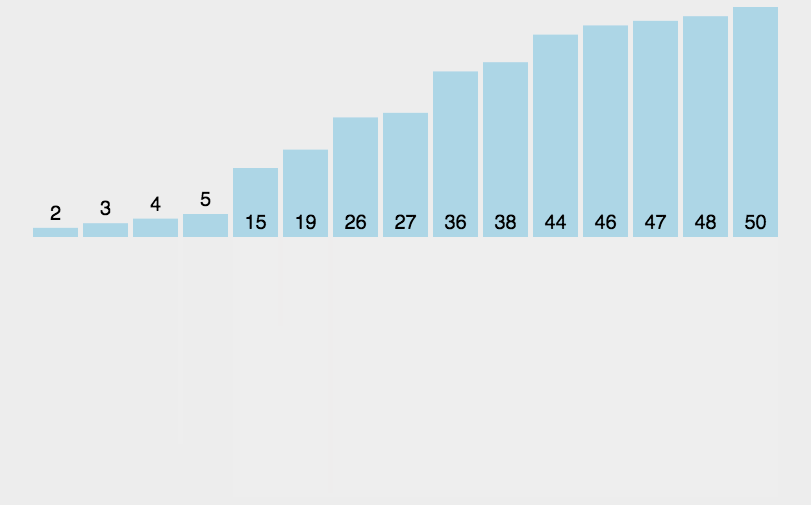
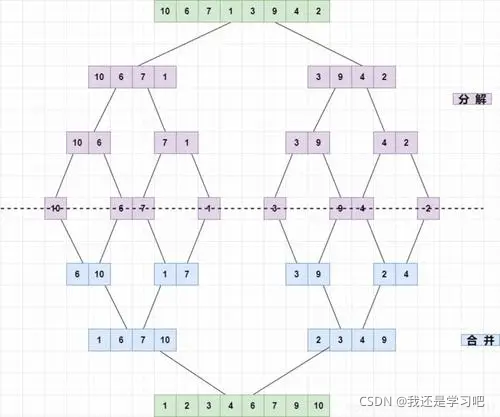
分析:
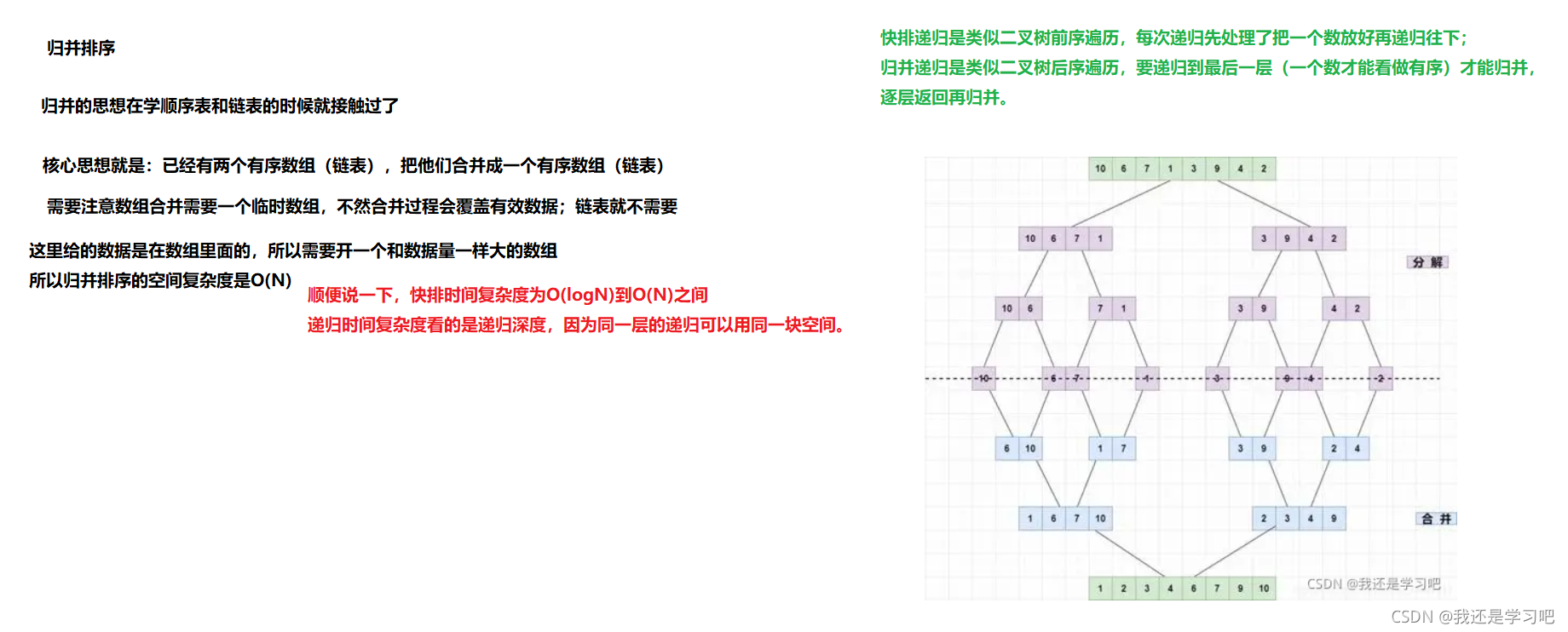
递归展开:
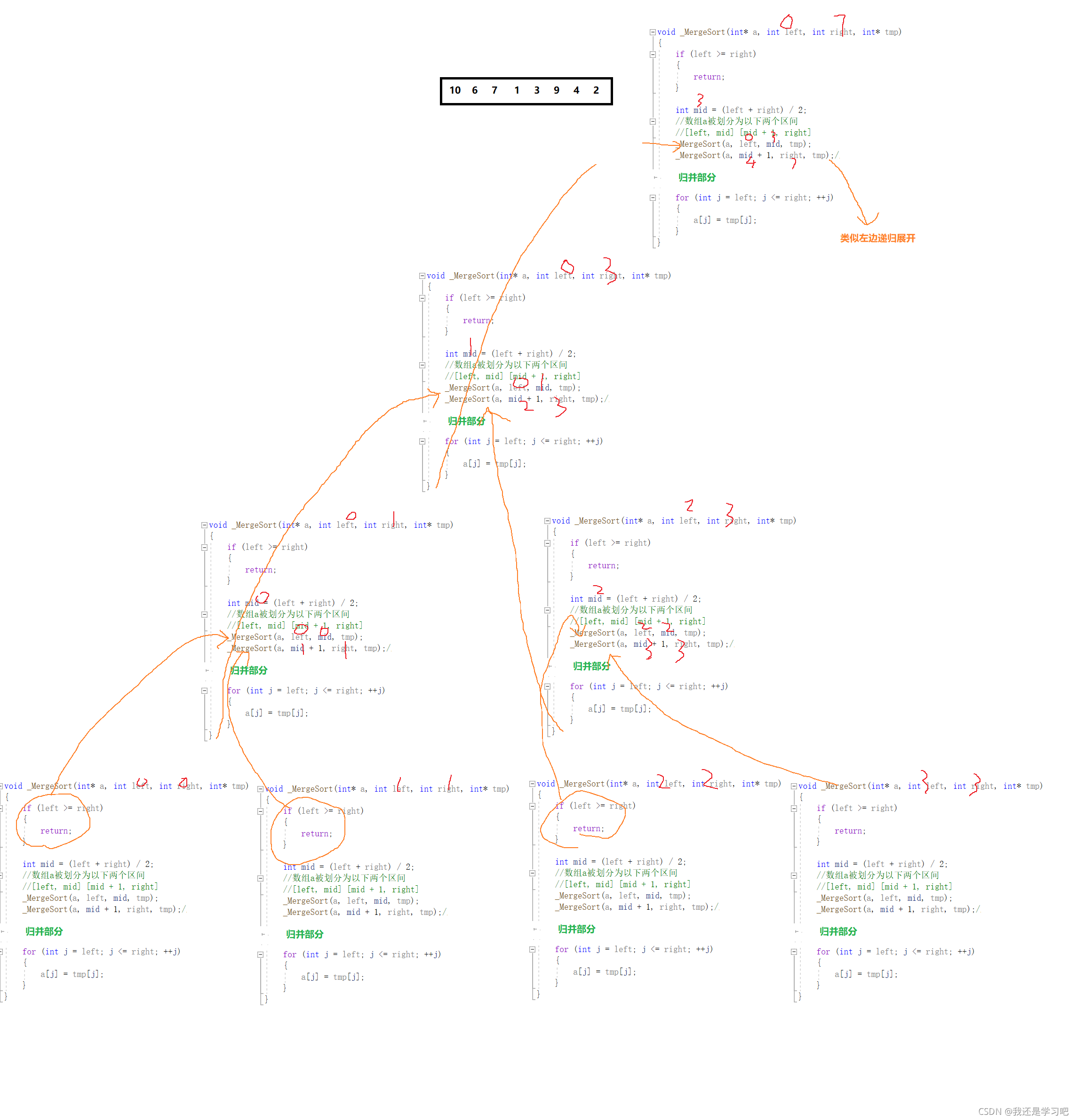
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//写子函数分区间递归
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
子函数
void _MergeSort(int* a, int left, int right, int* tmp)
{
//递归条件
if(left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
//左边有序、右边也有序,开始归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
while(begin1 <= end1 && begin2 <= end2)
{
if(a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while(begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while(begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//tmp的值拷贝回a,下一次归并要用
for(int j = left; j <= right; ++j)
{
a[j] = tmp[j];
}
}
归并非递归写法
分析:

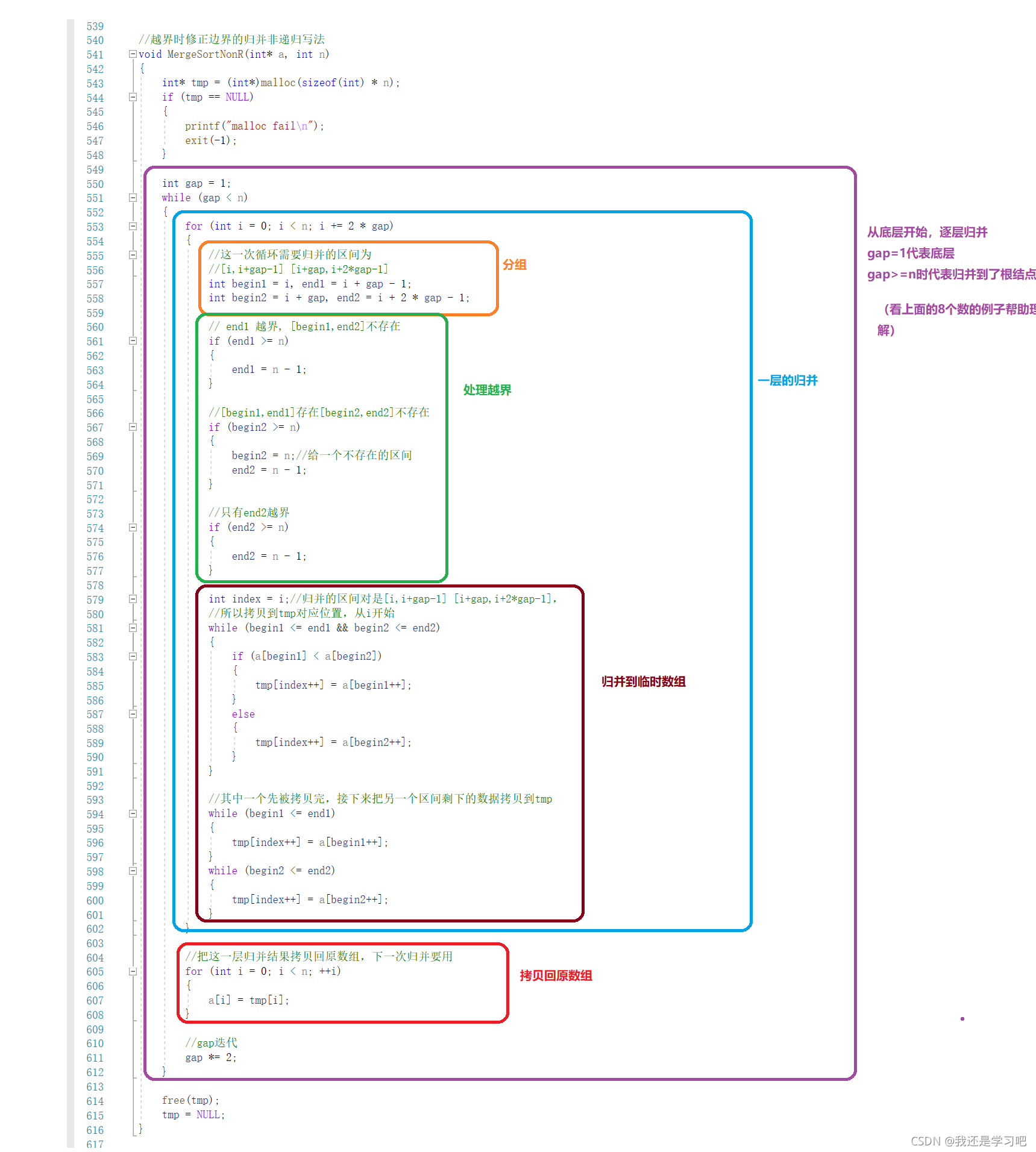
写法1
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while(gap < n)
{
for(int i = 0; i < n; i += 2 * gap)
{
//归并部分
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//越界处理
//end1越界
if(end1 >= n)
{
end1 = n - 1;
}
//end1未越界,begin2越界,给一个不存在的区间
if(begin2 >= n)
{
begin2 = n;//只要让begin2 > end2就行
end2 = n - 1;
}
//只有end2越界
if(end2 >= n)
{
end2 = n - 1;
}
//数据拷贝到临时数组的对应区间
int index = i;
//开始归并
while(begin1 <= end1 && begin2 < end2)
{
if(a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while(begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while(begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
//以上,便处理完了一层的归并
//把这一层归并结果拷贝回原数组,下一次归并要用
for(int i = 0; i < n; ++i)
{
a[i] = tmp[i];
}
//gap迭代
gap *= 2;
}
free(tmp);
tmp = NULL;
}
第二种写法
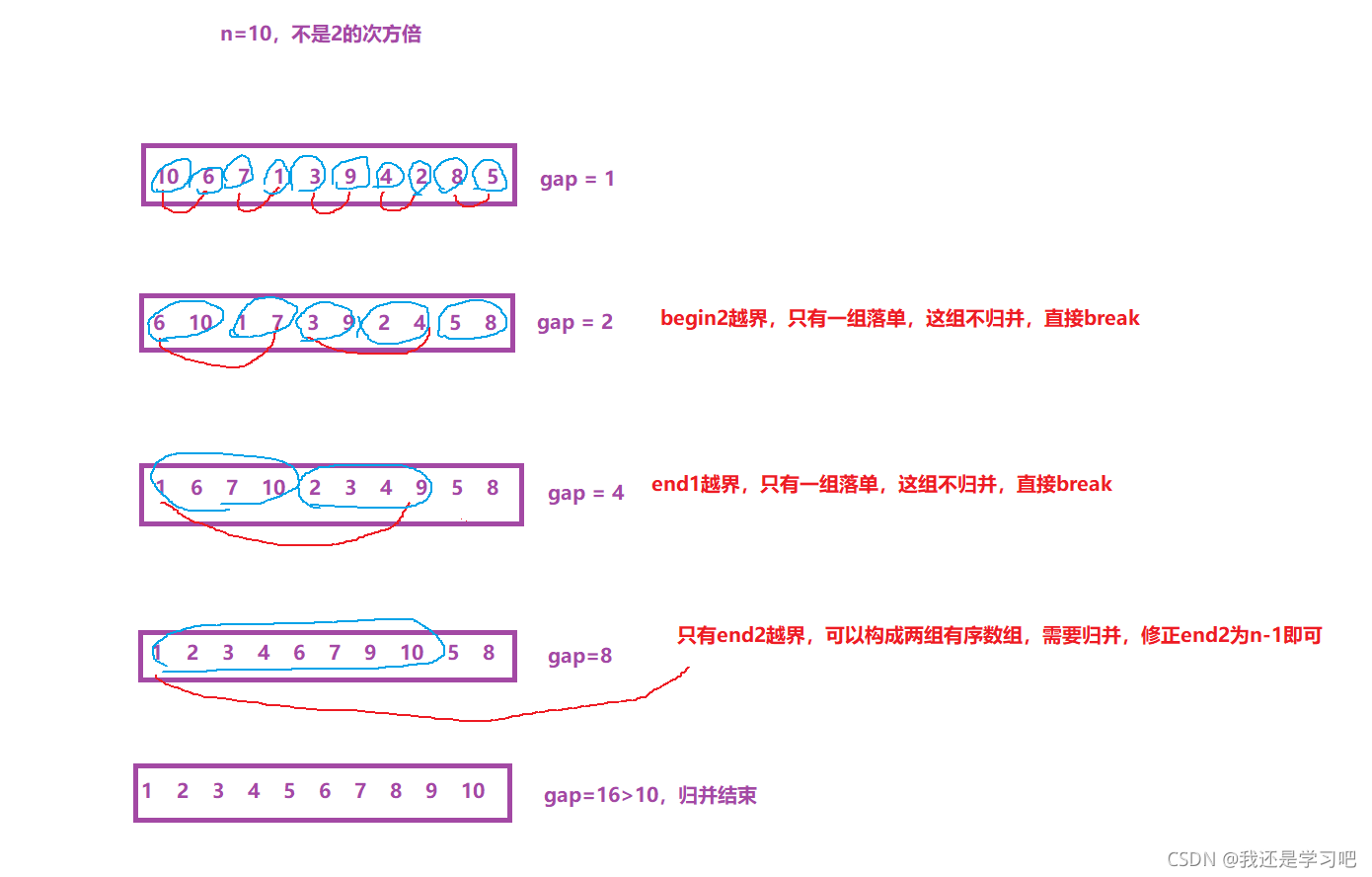
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while(gap < n)
{
for(int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//越界处理
if(end1 >= n || begin2 >= n)
{
break;
}
if(end2 >= n)
{
end2 = n - 1;
}
int index = i;
//开始归并
while(begin1 <= end1 && begin2 <= end2)
{
if(a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while(begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while(begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//归并完两组就拷贝回两组
for(int j = i; j < end2; ++j)
{
a[j] = tmp[j];
}
}
//下一层
gap *= 2;
}
free(tmp);
tmp = NULL;
}
计数排序
分析:
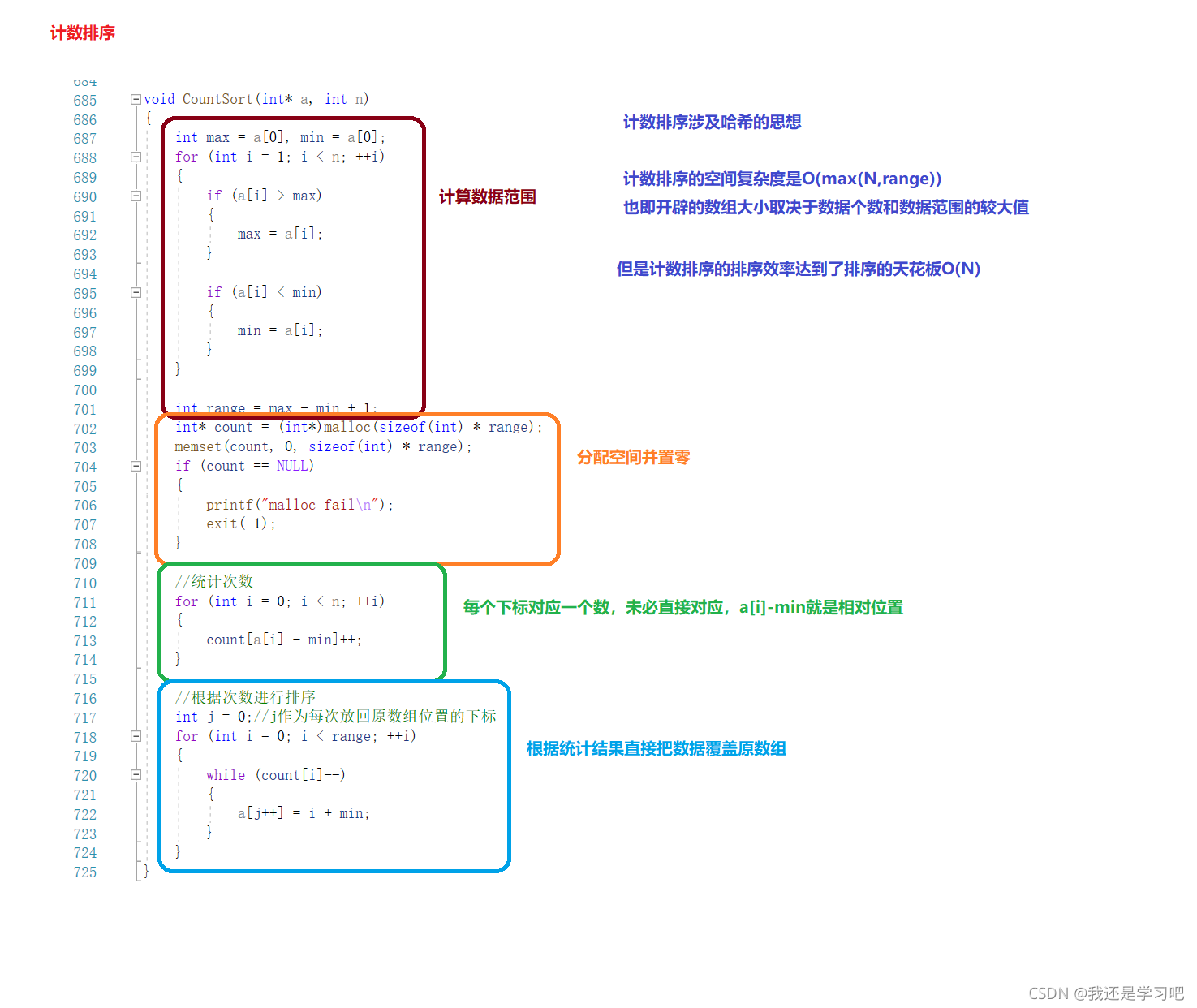
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);
if (count == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//统计次数
for (int i = 0; i < n; ++i)
{
count[a[i] - min]++;
}
//根据次数进行排序
int j = 0;//j作为每次放回原数组位置的下标
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}