1、基本概念
链式存储结构
\qquad
节点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻;
\qquad
线性表的链式表示又称为非顺序映像或者链式映像;
\qquad
用一组物理位置任意的存储单元来存放线性表的数据元素;
\qquad
这组存储单元既可以是连续的,也可以是不连续的,甚至是零散分布在内存中的任意位置上;
\qquad
链表中的元素的逻辑次序和物理次序不一定相同。
\qquad
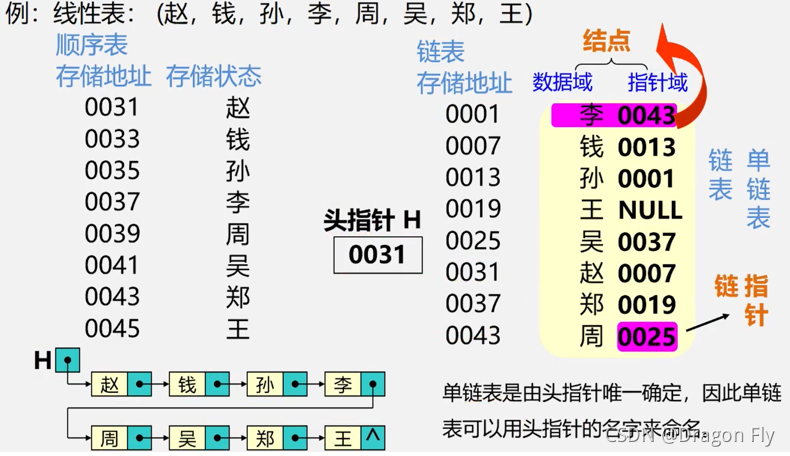
单向链表是由头指针唯一确定,因此单链表可以用头指针的名字来命名。
\qquad
结点: 数据元素的存储映像。由数据域和指针域两部分组成;
\qquad
链表: n个结点由指针链组成一个链表,它是线性表的链式存储映像,称为线性表的链式存储结构。
\qquad
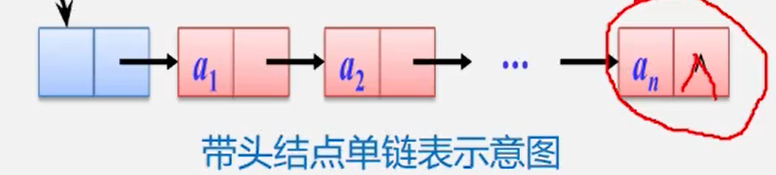
单链表: 结点只有一个指针域的链表,称为单向链表或者线性链表;
\qquad
双链表: 结点有两个指针域的链表;

\qquad
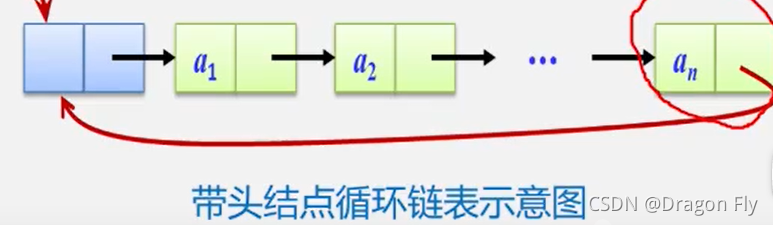
循环链表: 首尾相接的链表称为循环链表;
\qquad
头指针: 是指向链表中第一个结点的指针;
\qquad
首元结点: 是指链表中存储第一个数据元素
a
1
a_1
a1?的结点;
\qquad
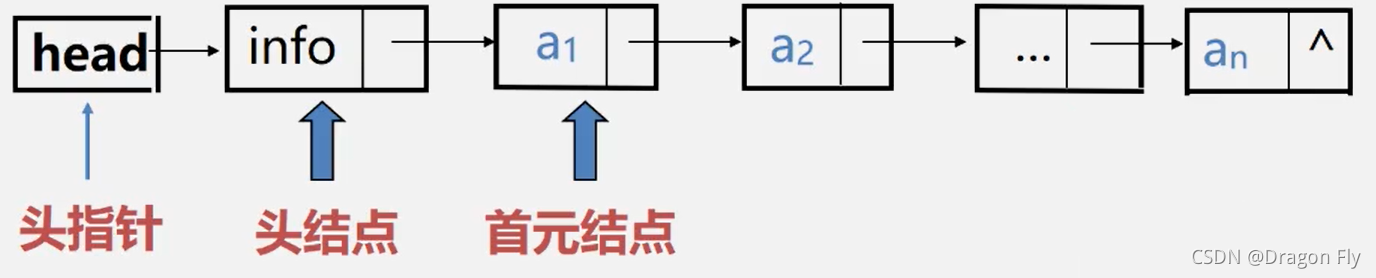
头结点: 是在链表的首元结点之前附设的一个结点;
\qquad
对于无头结点的单链表,头指针为空时表示空表;
\qquad
对于有头结点的单链表,当头结点指向空时,表示空表;
\qquad
添加头结点的好处: 首先便于首元结点的处理,首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其他位置一样,无需进行特殊处理;其次是便于空表和非空表的统一处理,无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了;
\qquad
头结点数据域存放内容: 头结点的数据域可以为空,也可以存放表长度等附加信息,但是注意头结点不计入链表的长度值;
链表的特点:
\qquad
结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻;
\qquad
访问时只能通过头指针进入链表,并通过每个节点的指针域依次向后顺序扫描其余结点,所以寻找第一个结点和最后一个结点花费的时间不同;(链表采用顺序存取法!顺序表示随机存取法)
2、带头结点的单向链表
\qquad
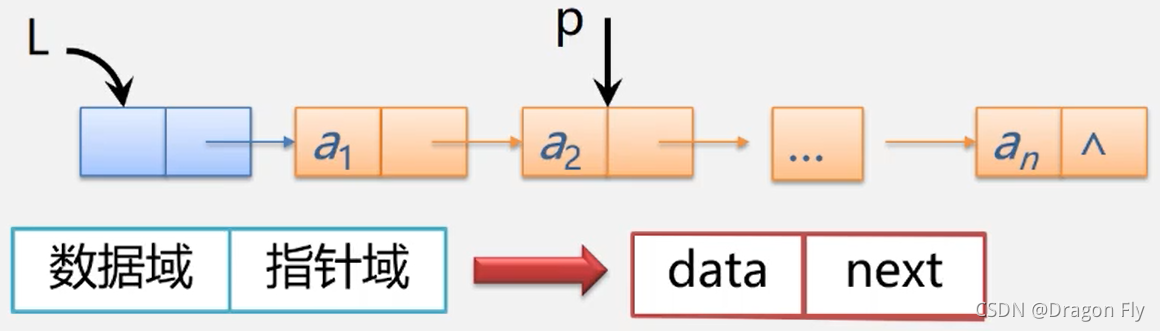
单向链表由表头唯一确定,因此单向链表可以用头指针的名字来命名。若头指针名是L,则把链表称为表L。
\qquad
单向链表的存储结构包括“数据域”+“指针域”两部分,其中“数据域”用来存放不同种类的数据,“指针域”存放一个结构体指针,指向下一个链表中的下一个结点。
//定义链表结构体
typedef class Lnode
{
ElemType data; //结点的数据域
Lnode *next; //结点的指针域
}Lnode, *LinkList;
单链表的初始化
\qquad
即构造一个空表,生成新节点作为头结点,用头指针L指向头结点,将头结点的指针域置空。
template <class Elem>
struct Node
{//结点定义
Elem data; //数据域
Node *next; //指针域
};
template <class Elem>
class MyList
{//链表定义
private:
Node<Elem> *head;
int cnt;
public:
MyList();
~MyList();
void IsEmpty(); //判断链表是否为空
};
template <class Elem>
MyList<Elem>::MyList()
{//链表的初始化
head = new Node<Elem>;
head->next = nullptr;
cnt = 0;
}
template <class Elem>
MyList<Elem>::~MyList()
{//析构链表,删除在类中申请的空间
Node<Elem> *rec = head;
while (rec != nullptr)
{
Node<Elem> *t = rec;
rec = rec->next;
delete t;
}
head = nullptr;
cnt = 0;
}
template<class Elem>
void MyList<Elem>::IsEmpty()
{//判断链表是否为空表
return head->next == nullptr;
}
template <class Elem>
void MyList<Elem>::Clear()
{//除了头结点之后,删除链表中的其他结点
Node<Elem> *rec = head->next;
while (rec != nullptr)
{
Node<Elem> *t = rec;
rec = rec->next;
delete t;
}
head->next = nullptr;
cnt = 0;
}
template<class Elem>
int MyList<Elem>::GetLength()
{//获取链表的长度
return cnt;
}
template<class Elem>
Node<Elem>* MyList<Elem>::GetAddress(Elem data)
{//按值查找某个节点,返回节点的地址
Node<Elem> *rec = head;
while (rec && rec->data != data)
rec = rec->next;
return rec;
}
template<class Elem>
int MyList<Elem>::GetIdx(Elem data)
{//按值查找某个节点,返回节点的索引
Node<Elem> *rec = head;
int n = -1;
while (rec != nullptr)
{
if (rec->data == data)
return n;
rec = rec->next;
++n;
}
return -1;//若链表中没有data,则返回-1
}
\qquad 因为线性表只能顺序存取,即在查找是要从头指针找起,查找的时间复杂度为 O ( n ) O(n) O(n)。
template<class Elem>
void MyList<Elem>::InsertElem(int i, Elem data)
{//在索引位置i之前插入元素Elem
if (i < 0)return; //插入位置有问题
Node<Elem> *rec = head;
int n = -1;
while (n < i-1 && rec)
{
rec = rec->next;
++n;
}
if (rec == nullptr)return;//插入位置有问题
//构建新的data节点
Node<Elem> *newNode = new Node<Elem>(data);
newNode->next = rec->next;
rec->next = newNode;
}
template<class Elem>
void MyList<Elem>::DeleteElem(int pos)
{//删除位置i的元素
if (pos < 0 || pos >= cnt)
{
cout << "删除位置不合理!" << endl;
return;
}
Node<Elem> *rec = head;
for (int i = 0; i < pos; ++i)
rec = rec->next;
Node<Elem> *toDel = rec->next;
rec->next = toDel->next;
--cnt;
delete toDel;
}
\qquad
因为线性链表不需要移动元素,只需要修改指针,所以链表插入和删除的时间复杂度为
O
(
1
)
O(1)
O(1)
\qquad
但是由于单链表进行插入和删除之前需要进行查找操作,由于要从头查找前驱节点,所耗费的时间复杂度为:
O
(
n
)
O(n)
O(n)
template<class Elem>
void MyList<Elem>::HeadInsert(Elem data)
{//头插法构建链表
Node<Elem> *nNode = new Node<Elem>;
nNode->data = data;
nNode->next = nullptr;
if (head->next == nullptr)
{
head->next = nNode;
++cnt;
return;
}
nNode->next = head->next;
head->next = nNode;
++cnt;
}
\qquad 头插法的时间复杂度为 O ( 1 ) O(1) O(1)。
template<class Elem>
void MyList<Elem>::My_PushBack(Elem data)
{//尾插法构建链表
Node<Elem> *nNode = new Node<Elem>;
nNode->data = data;
nNode->next = nullptr;
if (head->next == nullptr)
{
head->next = nNode;
tail = nNode;
++cnt;
return;
}
tail->next = nNode;
tail = nNode;
++cnt;
}
\qquad 链表尾插法的时间复杂度为 O ( n ) O(n) O(n)。